RLC串联谐振电路的工作原理及应用

1.串联谐振频率

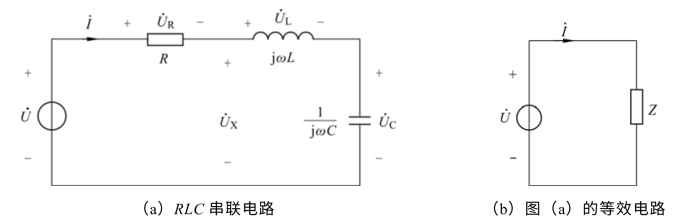
图3.53 RLC 串联谐振电路图

图3.53（a）电路KVL 电压关系为

图3.53（b）等效阻抗Z 为

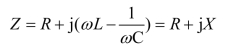
设图3.53（a）电路发生谐振（称为串联谐振），由等效阻抗Z 的虚部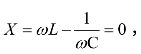得谐振角频率 ω0（或由 ω0=2πf0得 f0）为

结论：频率与电路性质关系：

2.串联谐振特征

（1）阻抗Z=R最小；电流有效值最大；cosφ=1、u 与i 同相位、电路呈阻性；Q=UI sinφ=0；uL与 uC大小相等相位相反，如图3.54 所示。

（2）储能不为零。

Q=QL+QC=0说明：电场能与磁场能相互转换，此增彼减，完全补偿。

（3）品质因素。

谐振时电感电压UL（或电容电压UC）与电路端电压U之比，称为RLC 串联谐振电路的品质因素，用Q 来表示，即(www.xing528.com)

图3.54 串联谐振时的相量图

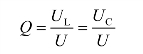
谐振时，如果品质因数Q >>1，电感和电容上会产生较高的电压。因此，在电子电路中充分利用谐振特性，接收、传输或放大信号；而在一些电气设备中，且要尽力避免谐振现象的发生，以免导致电气设备的损坏。

【例3.31】 某收音机的输入等效电路如图3.55（a）所示。已知R=8Ω，L=300 μH，C为可调电容器，电台信号 u1=1.5 mV，f1=540 kHz；u2=1.5 mV，f2=600 kHz。试求：

（1）当电路对信号 u1发生谐振时的电容值；

（2）当电路对信号 u2发生谐振时的电容值。

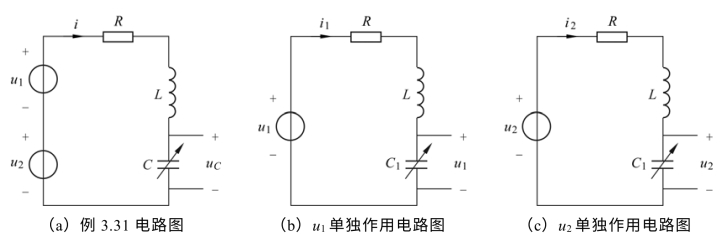
图3.55 例3.38图及解析电路图

分析：谐振时，频率与元件参数关系如式3.32 所示。

（1）根据信号u1发生谐振时的信号源频率 f1，解得图3.55（b）电路中电容 C1值。

（2）根据信号u2发生谐振时的信号源频率，解得图3.55（c）电路中电容 C2值。

解（1）对u1发生谐振电路如图3.55（b）所示。解电容 C1值为

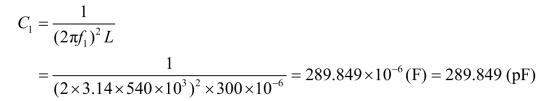
（2）对u2发生谐振电路如图3.55（c）所示。解电容 C2值为

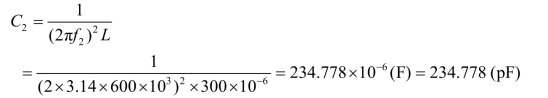
总结：根据谐振时电路的固有频率 ω0必须等于信号源频率 ωS（即 ωS=ω0）特性和电路的串联结构，计算电路元件的参数值。