无源RLC二端网络功率及其计算方法

无源RLC 二端网络N0如图3.45 所示，设

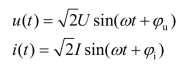
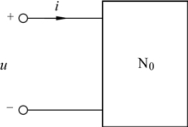
图3.45 RLC 二端网络N0

1.瞬时功率 p（t）

随时间而不断变化的功率称为瞬时功率 p（t）。即

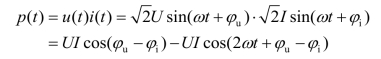
设φ=φu-φi，则

当 p（t）﹥0时，RLC 二端网络N0吸收能量；当 p（t） ﹤0时，RLC 二端网络N0释放能量。吸收与释放不断的交替，反映出电阻元件消耗能量、储能元件存储能量的物理特征。

在实际测量中，主要测量二端网络N0的有功分量能量和无功分量能量，即称为有功功率和无功功率。

2.有功功率P

电阻消耗的能量称为有功功率P，因其值P 是由 p（t）的平均值而得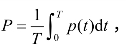又称为平均功率，即

式中，P 的单位为瓦特（W）；cosφ 称为功率因数；φ 称为功率因数角，即φ=φu-φi。其功率换算有

设图3.45 所示RLC 无源二端网络N0的等效阻抗为Z，即

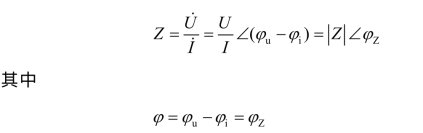
上式表明：功率因数角φ 等于电压与电流的相位差（φu-φi），也等于阻抗角 φZ。所以，功率因数cosφ的大小，由电路参数RLC、电源频率f 及电路结构所决定。

一般情况下，则0 ≤cosφ≤ 1，常用λ=cosφ表示功率因数。

（1）当电路为纯电阻（R）电路时，即Z=R，有

（2）当电路为纯电感（L）电路时，即Z=jωL，有

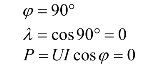
（3）当电路为纯电容（C）电路时，即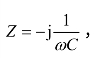有

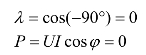
即电容和电感是储能元件，不消耗功功率，有功功率仅与电阻元件有关。

【例3.25】 电路如图3.46（a）所示。已知电压电阻R1=3Ω、R2=8Ω、感抗XL=4Ω、容抗XC=6Ω，试求电流i、i1、i2及电路的有功功率P。

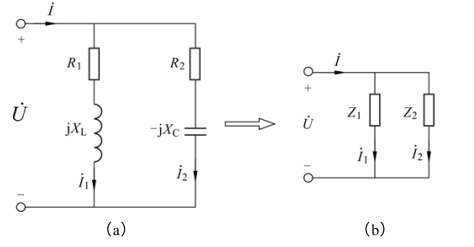
图3.46 例3.25图

分析：先分别计算RL、RC 串联电路等效阻抗 Z1、Z2，如图3.46（b）所示；根据广义欧姆定律计算电流；根据KCL 计算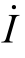电流；由电流写出电流i、i1、i2的表达式，并计算有功功率P=UIcos φ。

解（1）由 u（t）得相量式为

求解图3.46（b）中的等效阻抗 Z1、Z2。

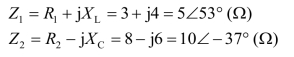
由广义欧姆定律得电流

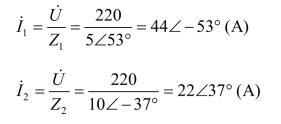
根据KCL 得

则电流的正弦式为

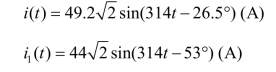
功率P

结论：

（1）有功功率还可以通过电路电阻元件计算，即

（2）通过RL 支路有功功率 P1=UIcosφ1和RC 支路有功功率 P2=UI2cosφ2之和计算功率P，即

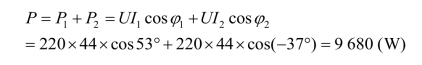
3.无功功率Q

在工程中还引用了无功功率的概念，用来反映电路与外界能量交换的最大速率，衡量电抗元件的功率特性，其定义为

式中，Q 称为无功功率，单位为乏（var）；φ 称为功率因数角。

（1）当电路为纯电阻（R）电路时，有

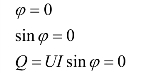
（2）当电路为纯电感（L）电路时，有

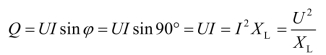
（3）当电路为纯电容（C）电路时，有

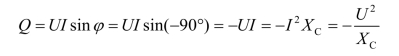
可见，电容C、电感L 元件中功率为无功功率Q。无功功率的大小表征出电路的性质，即

【例3.26】 电路如图3.47 所示，已知感抗XL=3Ω，容抗XC=8Ω，电阻R1=4Ω，R2=6Ω，电压源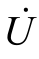=100∠0°。试求：(www.xing528.com)

（1）A、B 间电压UAB。

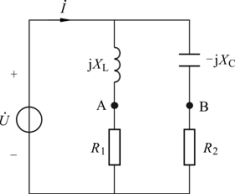
图3.47 例3.26图

（2）电路的有功功率P 和无功功率Q。

（3）说明该电路呈何性质？

分析：注意RL、RC 支路直接与电源并联；计算总电流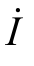后，用式（3.24）、式（3.25）计算有功功率P 和无功功率Q。

解（1）求UAB。

（2）求P 和Q。

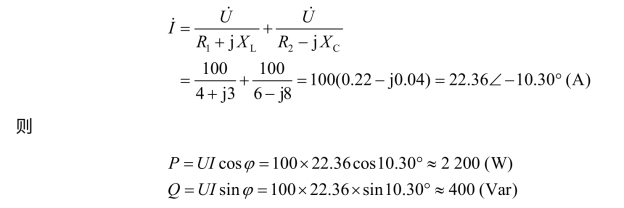
（3）电路性质。

因为，Q﹥0，所以电路呈感性。

4.视在功率

设电力设备所能达到的最大有功功率为设备的容量，称为视在功率S。即定义为

式（3.26）中，S 称为视在功率，单位为伏安（VA）。

有功功率P、无功功率Q、视在功率S 和功率因数角φ之间的关系，可以用功率三角形来表示。如图3.48 所示。其中S、P、Q 之间的数学关系为

功率因数cosφ 与S、P 之间关系为

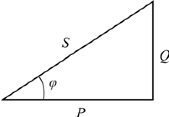
图3.48 功率三角形

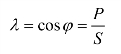
可见，功率因数cosφ 表示了P 与S 的比例关系。当P=S 时，λ=1，Q=0，电路呈阻性，为最理想的工作状态。

【例3.27】 试求例3.26 的功率因数和视在功率。

分析：由φ=φu-φi=0°-（-10.20 °）=10.30°得功率因数；由U=100 V 、I=22.36 A 得视在功率。

解 由功率因数角φ=10.30°得功率因数

视在功率

结论：功率因数角等于电压与电流的初相角之差，即φ=φu-φi。

5.复功率

复功率是功率的计算工具，即电压与电流的共轭量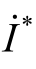之乘积，称为复功率，用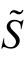表示。则复功率为

式（3.27）中，共轭电流量为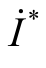=I∠-φiA，复功率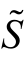单位为伏安（VA）。

复功率可通过P、Q、S 和功率因数角φ 解得，即

注意：

（1）复功率守恒、有功功率守恒、无功功率守恒。

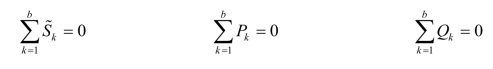
（2）视在功率不守恒。

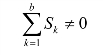
（3）复功率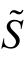不是正弦量功率，仅是一个辅助复数计算工具，没有物理意义。

【例3.28】 电路如图3.49 所示。已知电路中电压为电流为试求各元件有功功率、无功功率、视在功率，并判断其性质。

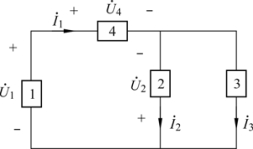
图3.49 例3.28图

分析：先根据电路连接的结构，应用KVL、KCL 解得电压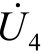和电流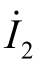；再通过复功率计算得元件功率及性质。

解 由KVL 得

由KCL 得

元件1 复功率为

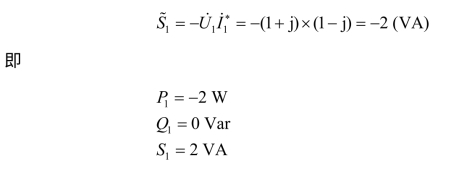
因为 P1﹤0，Q1=0 Var，元件1 提供2 W 功率，所以，元件1 为电源元件。元件2 复功率为

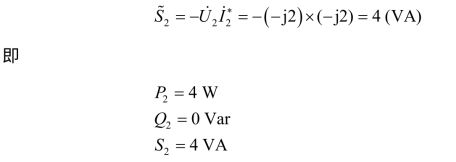
因为 P2﹥0，Q2=0 Var，元件2 消耗4 W 功率，所以，元件2 为电阻元件。元件3 复功率为

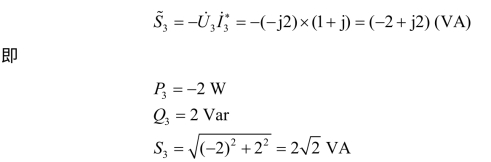
因为 P3﹤0，Q3﹥0，所以，元件3 为感性电源元件。元件4 复功率为

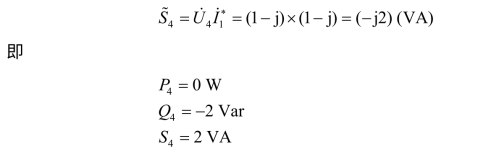
因为 P4=0 W，Q4﹤0，所以，元件4 为电容元件。

结论：根据复功率的计算结果，可直接得出有功功率P、无功功率 Q 、视在功率 S 和功率因数角φ，即如果在关联参考方向条件下，P﹥0，Q ﹤0，说明电路呈容性；P﹥0，Q﹥0，说明电路呈感性；P ﹤0，Q=0，说明电路呈电源性；P﹥0，Q=0，说明电路呈纯电阻性；P=0，Q ﹤0，说明电路呈纯电容性；P=0，Q﹥0，说明电路呈纯电感性；P ﹤0，Q﹥0，说明电路呈感性电源性。

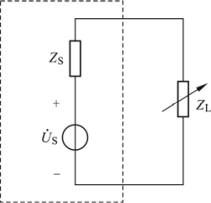
图3.50 最大功率的传输示图