RLC串联电路的特性分析

在正弦交流电路中，电路元件RLC 的基本连接方式有：串联、并联、星形和三角形连接；电压、电流关系中同样有分压、分流的基本概念。

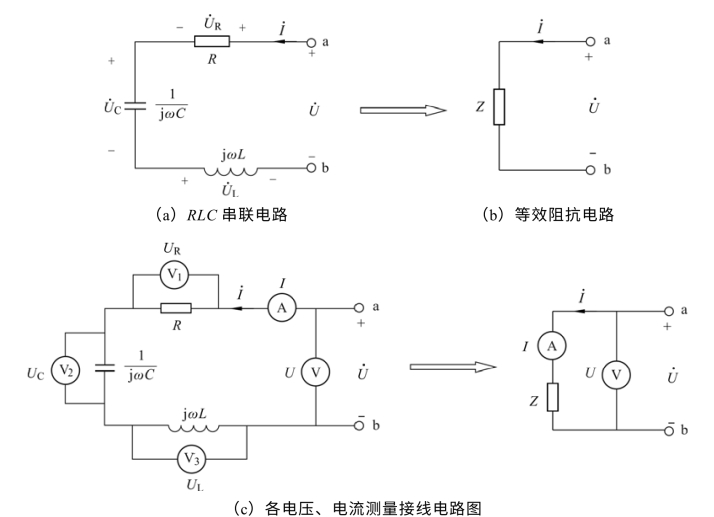
图3.30 RLC 串联电路与等效阻抗Z

RLC 串联电路如图3.30（a）所示，根据元件的伏安相量特性，有

其各有效值电压、电流测量电路如图3.30（c）所示；而总电压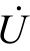由KVL 得

上式中，电抗阻抗Z 为

其等效阻抗Z 电路及有效值电压、电流测量电路如图3.30（b）（c）所示。

当图3.30（a）所示电路的频率f 一定时，元件RLC 参数的大小将决定其电路的性质，即

【例3.17】 RLC 串联交流电路如图3.30（a）所示，已知：R=30 Ω，L=127.39 mH，C=39 .81μ F，试求：

（1）电流的有效值I 和瞬时式i（t）。

（2）各元件上的电压有效值和瞬时表达式。

（3）画相量图。

（4）画测量各元件端电压的仪表接线电路图及测量值。

分析：

（1）根据电压 u（t）得相量。

（2）根据角频率ω=314 rad/s，计算感抗XL=ωL，容抗和阻抗Z=R+j（XL-XC）。

（3）根据广义的欧姆定律得电流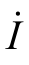、I 和i（t）。

（4）根据元件伏安相量特性解之各元件上的电压有效值和瞬时表达式。

解 根据 u（t）得

根据ω 得容抗、感抗为

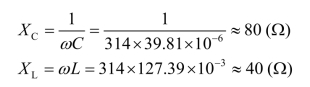
则RLC 串联电路等效阻抗为

（1）电流的有效值I 和瞬时值i（t）。

由广义欧姆定律得(www.xing528.com)

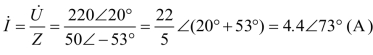
电流的有效值

电流的瞬时表达式

（2）各元件上的电压有效值和瞬时表达式。

电阻电压有效值

电阻电压瞬时表达式

电感电压有效值

电感电压瞬时表达式

电感电压有效值

电容电压瞬时表达式

（3）相量图如图3.31（a）所示。

（4）测量各元件端电压的仪表接线电路及测量值如图3.31（b）所示。

图3.31 相量图和测量电压图

结论：

（1）RLC 串联电路的计算，在形式上与电阻的串联电路计算相似，所不同的是，直流电路采用实数代数运算，相量电路采用复数数学工具。

（2）在同频率正弦交流中，

对于有n 个阻抗串联的电路[见图3.32（a）]，其等效总阻抗Z 为

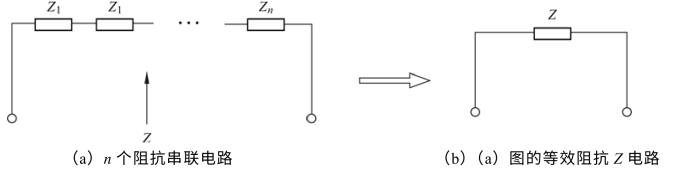
图3.32 n 个阻抗串联