【摘要】:式是欧姆定律的相量形式,称为广义的欧姆定律。阻抗模、电抗X、电阻R 和阻抗角 φZ之间的关系,可以用阻抗三角形来表示,如图3.29 所示。图3.29 阻抗三角形图3.29 阻抗三角形式中,G 称为电导,B 称为电纳,单位为西门子。 已知图3.28的电压、电流为=100 ∠ 45 °,=2∠-35°,试求二端相量网络N0的等效阻抗Z 和导纳Y,并判断电路的性质。解 根据式得等效阻抗Z。
用相量表示R、L、C 元件的伏安特性时,如图3.27 所示。
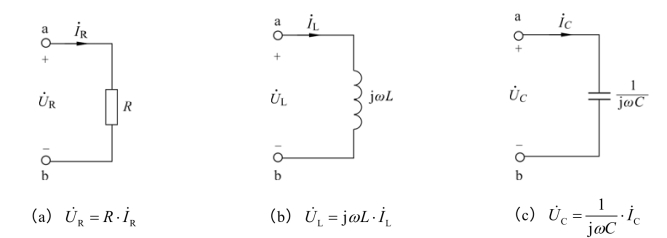
图3.27 相量电路图的伏安特性
当用RLC 构成一个无源线性二端相量网络N0时,如图3.28(a)所示。其二端相量网络N0对外电路可等效为如图3.28(b)所示电路,其参数Z 称阻抗,单位欧姆(Ω),Z 定义为

式(3.20)是欧姆定律的相量形式,称为广义的欧姆定律。
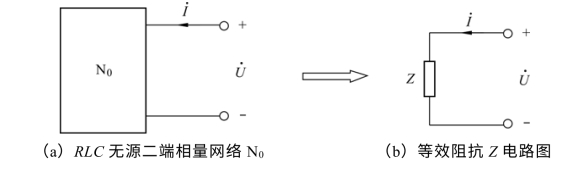
图3.28 阻抗Z 定义
设图3.28 电路中的电流![]() 电压
电压![]() 则对应的相量式
则对应的相量式![]() 代入式(3.20)得
代入式(3.20)得
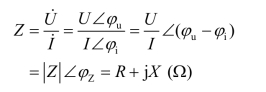
上式中,![]() 称为阻抗模,单位为欧姆(Ω);φZ称为阻抗角;R 称为等效电阻(阻抗实部);X 称为电抗(阻抗虚部),单位为欧姆(Ω)。
称为阻抗模,单位为欧姆(Ω);φZ称为阻抗角;R 称为等效电阻(阻抗实部);X 称为电抗(阻抗虚部),单位为欧姆(Ω)。
阻抗模![]() 和阻抗角 φZ参数的计算式分别为(https://www.xing528.com)
和阻抗角 φZ参数的计算式分别为(https://www.xing528.com)
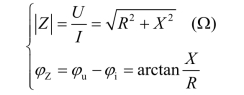
阻抗模![]() 、电抗X、电阻R 和阻抗角 φZ之间的关系,可以用阻抗三角形来表示,如图3.29 所示。
、电抗X、电阻R 和阻抗角 φZ之间的关系,可以用阻抗三角形来表示,如图3.29 所示。
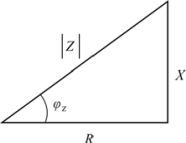
图3.29 阻抗三角形

式中,G 称为电导,B 称为电纳,单位为西门子(S)。
【例3.16】 已知图3.28(a)的电压、电流为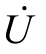 =100 ∠ 45 °(V),
=100 ∠ 45 °(V),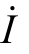 =2∠-35°(A),试求二端相量网络N0的等效阻抗Z 和导纳Y,并判断电路的性质。
=2∠-35°(A),试求二端相量网络N0的等效阻抗Z 和导纳Y,并判断电路的性质。
分析:直接运用广义的欧姆定律式(3.20)解之。
解 根据式(3.20)得等效阻抗Z。
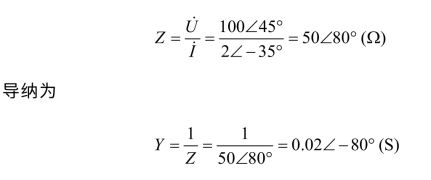
因阻抗角 φZ=80°﹥0,所以,电路的性质为感性。
结论:当阻抗角 φZ﹥0,电路呈现感性,电压u 超前电流i 相位80°,所以,无源二端网络N0的性质为感性。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




