基尔霍夫定律的相量式优化：简明介绍基尔霍夫定律

基尔霍夫定律的相量形式是分析与计算相量电路的基本定律，它包括基尔霍夫电流定律的相量形式和基尔霍夫电压定律相量形式。

3.4.1.1　基尔霍夫电流定律的相量式

1.KCL 的相量式

KCL：在正弦稳态电路中，任何时刻，流入任一结点的电流代数和恒等于零，即

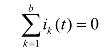
KCL 的相量式：在同频率的正弦稳态相量电路中，任何时刻，流入任一结点电流的相量和恒等于零，即

式（3.8）为KCL 有效值相量式；式（3.9）为KCL 最大值相量式。

【例3.10】 在同频率正弦交流电源激励下，稳态电路中某结点电流关系如图3.16 所示，试写出图中结点的KCL 方程，即写出方程。

图3.16 例3.10图

分析：书写结点KCL 方程时，注意设定一个电流参考方向（即“流入”或“流出”结点）为“正”。本题设流入结点的电流为“正”。

解图3.16（a）的KCL 方程：

图3.16（b）的KCL 相量式：

结论：列KCL 相量方程的方式方法与直流电路相似，所不同的是计算中采用的数学工具不同。

2.KCL 拓展与应用

1）结点的拓展

在同频率的正弦稳态相量电路中，任何时刻，流出结点电流等于流入该结点的电流。即

【例3.11】 电路如图3.17（a）所示，已知电流源电流电阻R 电流试求电压源 uS（t）中的有效值电流IU和瞬时值电流 iU（t），并画出测量电流IU的接线电路图。

图3.17 例3.11图

分析：首先将图3.17（a）转换为相量电路图3.17（b），再根据KCL 相量式求解。

解 画相量电路图，如图3.17（b）所示，其已知相量式为

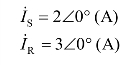
根据KCL 得

(www.xing528.com)

有效值电流IU为

瞬时值电流 iU（t）为

电流表测量接线电路如图3.17（c）所示。

结论：如已知电路中的电量为正弦电量时，解题时首先将正弦电量转换为相量式，再根据电路结构分析相量电路。正弦交流电路电流表测量的值为电流有效值，其连接方式与直流电表相同，即串联在被测电流支路中。

2）结点拓展到封闭面

KCL 相量式推广到封闭面：在同频率的正弦稳态相量电路中，任何时刻，流出封闭面的电流相量等于流入该封闭面的电流相量。

2.4.1.2　基尔霍夫电压定律的相量式

1.KVL 的相量式

KVL：在正弦稳态电路中，任一时刻，沿任一闭合路径的电压代数和恒等于零，即

KVL 的相量式：在同频率的正弦稳态相量电路中，任何时刻，任一回路中的电压相量和恒等于零，即

式（3.10）为KVL 有效值相量式；式（3.11）为KVL 最大值相量式。

【例3.12】 试列出如图3.18（a）所示电路中回路1、2、3 的电压相量方程，并画出测量电压U 的接线电路图。

图3.18 例3.12图

分析：

（1）图3.18（a）所示回路1、2、3 中，均以顺时针方向标定了其电压降的绕行方向，则可沿着这个设定的顺时针绕行方向列KVL 相量方程。

（2）关联参考方向下，电阻元件上伏安相量特性为：

解 列KVL 相量方程。

测量电压U 的接线电路如图3.18（b）所示。

结论：在列KVL 相量方程时，可以根据所设定的回路绕行方向列回路的KVL 相量方程。当绕行方向是由电压的“+”极指向“－”极时，KVL 相量电压为“+”，否则相量电压为“－”。

2.注 意

（1）在列KVL 相量方程时，涉及相量电压参考方向和回路绕行方向的假设。回路绕行方向和相量电压参考方向都可以任意假设，但是一旦确定，在整个分析过程中不能更改。

（2）在正弦稳态相量电路中，结点电流的相量满足KCL，而结点电流的有效值一般不满足KCL；同理，回路电压也只有相量值才满足KVL。