复数的极坐标式及运算法则

相量是正弦交流稳态电路分析计算的一种有效的数学工具，其运算是通过复数运算来实现的。

1.复数表达式

复数式可分为四种表达式：代数式、极坐标式、三角式和指数式，其中，j 表示复数的虚数单位。

1）代数式

图3.13 复平面

上式中，a 为实部，b 为虚部。在如图3.13 所示的复平面上，横轴为实部a，纵轴为虚部b，其平行四边形的对角线为复数。

2）极坐标式

根据图3.13 可得复数的极坐标式，为

上式中，A 称为复数的模，φ称为复数的辐角，其计算关系式为

3）三角式

由图3.13 中直角三角形分析得

则三角式为

4）指数式

由欧拉公式，得

【例3.7】 已知电压的相量式=220ej30°（V），电流的相量式=（-4-j3）（A），试分别写出其他几种复数表达式。

解 电压的相量式

电流的相量式

结论：复数的代数形式转换为极坐标形式的时，特别要注意复数的辐角所在的象限，即第一象限、第二象限角度为正角度值；第三象限、第四象限的角度为负角度值，如图3.14 所示。

图3.14 复平面上复数的辐角与复数式

2.复数四则运算

已知：(https://www.xing528.com)

1）和差运算

即用代数式进行复数的和差运算：实部与实部相加减，虚部与虚部相加减。

复数的和差运算也可以用平行四边形法。如图3.15 所示。

图3.15 复数运算的图解法

2）乘除运算

即用极坐标式进行复数的乘法和除法运算：乘法运算为模相乘，初相位相加；除法运算为模相除，初相位相减。

【例3.8】 已知复数试求它们的和、差、积、商。

结论：一般“和、差”运算时，采用复数的代数形式；而“积、商”运算时，则用复数的极坐标式。

3.正弦量的微分与相量式

设：其对应的相量式为

i（t）微分为

上式的相量式为

将式=I ∠φ代入上式，得

可见，i（t）相量式乘以jω等于所对应的相量式。如表3.1 所示。

表3.1　正弦函数式与相量式对应关系

4.虚数运算

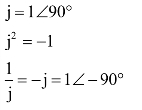
【例3.9】 已知正弦交流电流试求i（t）=i1（t）+i2（t）。

分析：首先将正弦电流量转换成有效值相量式电流量；其次，因两个电量是加法运算，所以相量式应写成代数式。

结论：正弦函数式的加减运算，可借用相量运算工具来完成，其解题步骤为：先将“时域式”转换成“相量式”，再进行相量式运算，最后将“相量式”变换成“时域式”。