相量工具的基本概念

正弦量的三个要素中的频率f 是由电源所给定，在整个同频率的正弦稳态电路分析中，其电路的频率始终保持不变，因此，重点是分析计算最大值（或有效值）和初相位两个参数。

注意：最大值（或有效值）和初相位都是常量。

1.相量表达式

设有一复数指数为则由欧拉公式得

式（3.7）中的 Imcos（ωt+φi）为复数的实部，Imsin（ωt+φi）为复数的虚部；可见，无论是复数的实部还是虚部，其运算式都是正弦函数形式，即可引用欧拉公式来分析正弦交流电路。

在同频率正弦稳态电路中，因角频率ω 是一个已知常量，所以，式（3.7）中 ejω　t为已知量，而最大值 Im、初相位 φi是未知的常量，即Imejφi为一个复常数，称复常数Imejφi为相量。在电路中，可用变量“最大值相量”或“有效值相量I”符号表示。

例如，有一正弦交流电流为其相量式为

最大值相量式：

有效值相量式：

2.相量图

相量式在复平面上用“有向线段”表示的图形称为相量图。如图3.11 所示。

例如：设的相量式为

图3.11 相量图

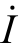设0﹤φi﹤90°，在复平面坐标下，用相量线段的长短表示有效值I；用线段与实轴的夹角表示初相位 φi，则相量式的相量图如图3.11 所示（注意：横轴为实轴，纵轴j 为虚轴）。

注意：

（1）相量式可用最大值相量式或有效值相量式表示。

（2）在电路分析中，注意采用同一种相量形式，即电压、电流都用有效值相量式，或都用最大值相量式。

（3）相量仅是正弦量的一种数学计算工具。

3.例 题

【例3.5】 试写瞬时表达式的相量表达式。

分析：(www.xing528.com)

（1）在表达式中，V 为最大值；10 V 为有效值；90°为初相位。

（2）在 u2（t）=20sin（ωt-135°）（V）表达式中，20 V 为最大值；V 为有效值；-1 35°为初相位。

解（1）

有效值相量式

最大值相量式

（2） u2(t)=20sin(ωt-135 °)(V)。

有效值相量式

最大值相量式

结论：由正弦函数式写相量式时，关注正弦量的最大值或有效值、初相位。

【例3.6】 已知电流试求频率f、有效值I、初相位φ和相量式，并画出电流 i1（t）、i2（t）的相量图，比较它们相位关系。

分析：i1（t）、i2（t）的频率相同，则可根据ω=2πf解得频率f；根据电流 i1（t）、i2（t）式得有效值I、初相位φ；根据相量式可画出相量图，并判定两个电流间的相位关系。

解 频率f 为

由 i1（t）得

由 i2（t）得

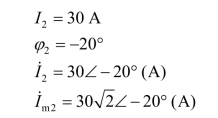
图3.12、的相量图

相量图如图3.12 所示，i1（t）引前 i2（t）相位50°；或者说，i2（t）滞后 i1（t）相位50°。

结论：相量图非常直观地展示出正弦量之间的相位关系，同时，也可以通过作相量图解得各相量值，这种方法称为相量图解法。