正弦函数的基本概念与性质

正弦波：随时间t 按照正弦规律变化的物理量，称为正弦量，其波形称为正弦波。如图3.7 所示的波形为正弦电流波形图，图3.7（b）的正弦函数表达式为i（t）=Imsin（ωt+φi）。

图3.7 正弦电流波形图

1.正弦函数的三要素

下面以i（t）=Imsin（ωt+φi）表达式为例，讨论瞬时值i（t）、幅值Im、角频率ω、初相位 φi等基本概念。

瞬时值：i（t）表示时间函数的正弦量，它表示了在某时刻的电流值，称为t 时刻的瞬时值。在电路分析中，规定用小写字母i、u 表示的电流、电压为正弦函数电量。

幅值：Im表示正弦波的最大值，或称振幅、峰值。即相对零值而言正弦波的最大值，对于给定的正弦波，其幅值是恒定的，如图3.7（a）所示。

角频率：ω是正弦波的角频率，它反映了正弦波变化的快慢。其单位为弧度/秒（rad/s）。

式中：T 表示正弦波完成一个循环变化所需的时间，称为周期，单位为秒（s），如图3.7（a）所示；f 表示正弦波在1 秒内完成的周期数，称为频率，单位为赫兹（Hz）。

我国工业供电系统提供的正弦交流电的频率为50 Hz，习惯上称之为工频。

初相位：φi表示正弦函数i（t）在t=0 时的相位，称为初相位。初相位的取值范围一般为单位为弧度或度。如图3.7 所示。

例如，对于正弦电流i（t）=Imsin（ωt+φi），有

当φi=0时：

当φi=135°时：

当φi=-8 5°时：

正弦函数也可用余弦函数来表示，即

所以，在电路分析中，可以用余弦函数或正弦函数来表示一个正弦交流电量，并统称为正弦交流电路。

由于幅值Im、角频率ω、初相位 φi决定了正弦交流电的瞬时值i（t），因此，将幅值、角频率和初相位称为正弦函数的三要素。

【例3.1】 已知正弦交流电流为i（t）=5sin（314 t+30°） A，试求其电流的最大值 Im、角频率ω、频率f 、周期T 和初相位 φi。

分析：在i（t）=Imsin（ωt+φi）式中，Im为最大值；ω 为角频率；φi为初相角。

解

结论：正弦交流函数表达出电量的最大变化范围，即最大值；正弦波变化的快慢，即角频率；正弦波完成一个循环变化所需的时间，即周期；正弦波在1 秒内完成的周期数，即频率；t=0 时的相位，即初相位。

【例3.2】 已知正弦交流电流的幅值频率f=50 Hz，初相角φi=30°，试写出正弦交流电流的瞬时表达式，并画出波形图。

分析：正弦交流电流的表达式为i（t）=Imsin（ωt+φi），其中角频率为ω=2πf。

解

瞬时表达式i（t）为

其波形如图3.8 所示。

结论：根据正弦量的三要素，可以直接写出正弦量的瞬时表达式。

图3.8 正弦交流电流i（t）的波形图

2.相位差

同频率下的不同正弦波（或不同余弦波）之间初相位之差称为相位差。例如，设有两个正弦交流量为

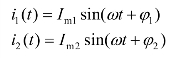
其相位差 φ12为

即在同频率条件下，相位差等于初相位之差，与正弦交流量的频率大小和变化时间无关，即相位差是一个常量。

一般，两个正弦波的相位关系可以分为三种情况，如图3.9 所示。(www.xing528.com)

（1） φ12=φ1-φ2﹥0时：φ1﹥φ2，称i1超前（或引前）i2，或者称i2滞后i1，如图3.9（a）所示。

（2） φ12=φ1-φ2=0时：φ1=φ2，称i1与i2同相，如图3.9（b）所示。

（3） φ12=φ1-φ2=180°时：φ1=-φ2，称i1与i2反相，如图3.9（c）所示。

图3.9 相位差

【例3.3】 已知电压 u（t）=8sin（ωt+30°）（V），电流 i1（t）=5sin（ωt+50 °）（A），电流i2（t）=10cos（ωt-90 °）（A），试计算电压 u（t）与电流i1（t）、i2（t）间的相位差，并说明其相位关系。

分析：电量 u（t）、i1（t）、i2（t）的角频率为ω，即三个电量为同频率电量。注意 i2（t）为余弦函数，要转换成正弦函数。

解u（t）与 i1（t）间的相位差 φ1为

即电压 u（t）滞后电流 i1（t）相位20°。

u（t）与 i2（t）间的相位差 φ2为

即电压 u（t）引前电流 i2（t）相位30°。

结论：

（1）相位差必须在同频率条件下进行计算，并且相位差是一个常数。

（2）相位差分析时注意必须是相同的函数。

3.有效值

在工程上，人们关心交流电所产生的效果，其效果常用有效值和平均值来表示。例如，人们常说照明电路的电压是220 V，指的是正弦交流电压所产生的有效值效果。各种正弦交流电的电器设备上所标的额定电压和额定电流均为有效值。另外，利用交流电流表和交流电压表测量的交流电流和交流电压也都是正弦交流电的有效值。

有效值：又称为均方根值，是按等值热效应概念来定义的，即是正弦波热效应的度量。

例如：在图3.10（a）所示电路中，当电阻R 与正弦交流电压源 uS（t）连接，在一周T 内，其电流i（t）=Imsin（ωt+φi）在电阻R 上产生的热量为

在图3.10（b）所示电路中，当同一个电阻R 连接于直流电压源US上，在相同的时间周期T 内，其直流电流I 在电阻R 上产生的热量为

图3.10 当电阻R 产生相同热量时，有效值等于直流电量

由在相同电阻R 上产生相同热量 Q1=Q2，得

解上式得

将i（t）=Imsin（ωt+φi）代入上式，得

即正弦交流电流和直流电流流过等值R 的电阻，在相同的时间周期T 内，当两者产生的热效应相等时，称直流电流I 为周期电流i 的有效值。其电流正弦量的有效值I 与最大值Im的关系为

同理，正弦交流电压的有效值与最大值的关系有

另：由图3.10 所示电压表、电流表接线电路可知，测量仪表的连接方式方法相同，即电压表与被测电压端并联，电流表串联于被测电流支路中。所不同的是，直流电表在连接时应注意被测直流电压的“正、负”极性、直流电流的方向。

【例3.4】 已知正弦电流的有效值I=5 A，频率f=50 Hz，初相位φi=-45°，试写出正弦电流i（t）表达式。

分析：最大值与有效值的关系为：

解 最大值为

角频率为

则i（t）为

结论：当已知正弦量的三要素（最大值或有效值、角频率和初相角）时，可以直接写出正弦量的瞬时表达式（三角函数式）。