电容元件的结构和特性探究

1.电容元件的基本概念

实际电容器是由用某种绝缘介质隔开的两个理想导电极板构成，如图3.1（a）所示。在外电路的作用下，两个极板上分别聚集起等量的正、负电荷q，并在介质中建立电场而具有电场能量。将外电路移去后，电荷依靠电场吸力可继续聚集在极板上，电场继续存在。因此，电容器是一种储存电荷或者说储存电场能量的部件，如图3.1（b）所示。

图3.1 电容元件结构及电场特性

电容元件是表征储存电场能这一物理特征的电路模型。电路分析中讨论的是在理想条件下抽象化的线性电容元件。

2.电容元件的定义

线性电容（简称电容）元件的电路符号、电压和电流参考方向如图3.2（a）所示，特性曲线如图3.2（b）所示，即特性曲线在q-u 平面上任意时刻t 都是过原点的直线。

图3.2 线性电容元件

电容元件由电容电荷q 与电容端电压u 的正比关系来定义，即

式中，C 称为电容值，是一个正实常数，单位为法拉（F）。实际电容值的大小常常为10－6F或10－12F数量级，即

3.电容元件的伏安特性

在电路分析中，主要研究电容元件的伏安关系。如果电容元件的电压u 和电流i 取关联参考方向，如图3.2（a）所示，则伏安关系为

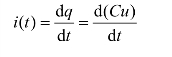
因C 为常数，即

式（3.1）表明：(www.xing528.com)

（1）通过电容C 某时刻的电流i 与该时刻其端电压u 的大小无关，而是与端电压u 的变化率成正比。

（2）当电容C 端电压u 不随时间变化时，电流i 为零。即端电压u 为直流电量时，通过电容C 的电流电容C 等效为开路。所以，常称电容元件具有隔断直流（在电子技术中简称隔直）的作用。

注意：当采用非关联参考方向时，如图3.3 所示，式（3.1）前需加负号，即

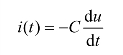
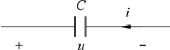
图3.3 非关联参考方向

电容C 两端的电压 u（t）可由式（3.1）得

式（3.2）中u（t0）常称为初始电压值，当 t0=0时，有

可见，电容C 电压 u（t）大小与t=-∞至t 时段中所通过的电流有关。因此，电容元件是一种有“记忆”的元件。

4.电容元件的功率与电能

在电压u 和电流i 关联[见图3.2（a）]参考方向下，电容元件的瞬时吸收功率为

当 p（t）﹥0时C 元件吸收功率，储存的电场能量增加，称这一种状态为“电容充电”；当p（t） ﹤0时C 元件释放功率，释放储存的电场能量，这时称为“电容放电”。由于理想电容不消耗能量，只储存电场能量，因此，电容元件属于储能元件。

电容元件从0 到t 时间内吸收的电能为

上式表明：任意时刻电容元件的储能 w（t）≥0，因此，电容元件属于无源元件。