最大功率传输定理解析与应用

电子电路分析中，常常关注负载上是否能获得最大功率。因此，在讨论有关电子电路获得最大功率问题时，将电子电路分解为两个电路模块，即：给负载提供功率的电路模块NS和负载电路模块RL。其中，模块NS总可以用戴维南等效电路来替代（如图2.33 所示）。这样，电子电路获得最大功率的问题转化为电路理论中最大功率传输定理。

最大功率传输定理：设有一个电压源模型与一个电阻负载相接，当负载电阻等于电压源模型的内电阻时，则负载能从电压源模型中获得最大功率。

例如：在图2.33 所示电路中，当RL=RS时，

负载RL上获得最大功率为PLmax，有

图2.33　电压源模型与负载RL

负载获得最大功率状态又称为负载与电源相匹配。

【例2.12】 在图2.34 所示电路中，当可变电阻RL等于多大时它能从电路中吸收最大的功率，并求此最大功率。

图2.34　例2.12 电路图

分析：利用戴维南定理将电阻 RL之外的电路用戴维南等效电路替代，再根据最大功率传输定理，得吸收最大的功率的电阻 RL值及最大功率。

解 （1）计算戴维南等效电路。

求解图2.35 中的开路电压UAB(www.xing528.com)

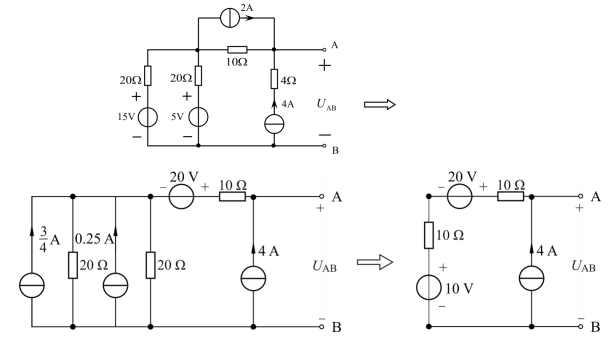
图2.35　等效变换法求开路电压UAB电路图

求解图2.36 中的等效电阻 R0

图2.36　求戴维南等效电阻电路图

图2.37　戴维南等效电路

解图2.37 得获得最大功率的负载RL为

负载RL上获得的最大功率Pmax

结论：戴维南定理不仅能分析电流、电压，还可应用于分析最大功率的传输电路。