电阻并联：等效电阻和各支路电流计算

1.电阻并联电路图

当3 个电阻同时连接在两个结点之间（见图1.60）时，形成三条支路，这三条支路具有相同的电压，则称3 个电阻的连接方式为并联。

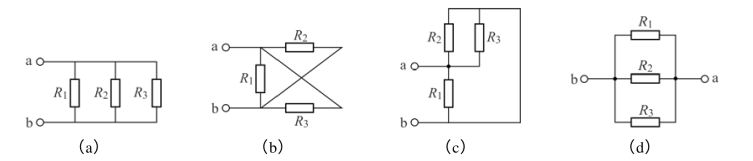
图1.60　3 个电阻并联电路图

图1.60 展现了4 个不同几何图形的并联电路，4 个电路的连接结构（并联）和电压特性（每一条支路电压都相等）是完全相同的。

并联电阻之间的关系常用两条平行直线“//”来表示，例如图1.60 中相互并联的电阻关系，可表示为

2.并联电阻的总电阻

若有n 个电阻连接在两个结点之间，其电阻之间的电压都是相等的，则称这n 个电阻的连接方式为并联。如图1.61（a）所示。

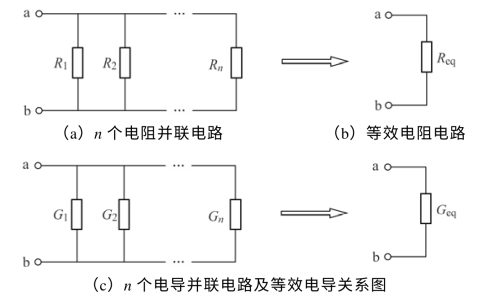
图1.61　并联电阻电路及等效电路图

图1.61（a）所示电路的总电阻Req的倒数等于各个电阻值的倒数之和，即

由式（1.15）得图1.61（b）总电阻Req值的计算式为

当图1.61（a）中的并联电阻相等时，即 R1=R2=…=Rn=R，则总电阻为

令式（1.15）中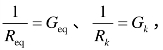其 Geq、Gk称为电导，则图1.61（c）所示电路的总电导为

式（1.18）中电导 Geq的单位为西门子（S）。

若图1.61（c）中 G1=G2=…=Gn=G，则由式（1.18）得总电阻为

【例1.16】 电路如图1.62 所示，已知电阻 R1=3Ω，R2=6Ω，试求等效电阻Rab。

分析：计算等效电阻的电路图，常常直接用如图1.62 所示电路形式表示。根据式1.16得等效电阻为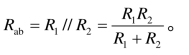

解

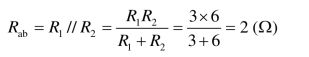
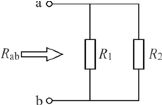
图1.62　例1.16图

结论：n 个电阻并联的电路，对外电路可用一个电阻等效替代。

3.电阻并联的分流作用

并联电阻电路中，各并联支路的端电压是相等的，如图1.63 所示电路中电阻 R1至 Rn的端电压都等于U。其电流关系可根据KCL 得

根据欧姆定律，总电流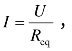支路电阻Rk上的电流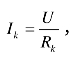则

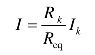
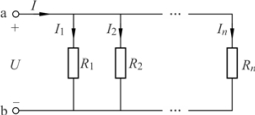
图1.63　并联电阻电路

上式中电阻 Req为并联电路的等效总电阻。则各支路电流 Ik的计算式为

式（1.20）称为电流分配公式，或称分流公式。式（1.20）说明各个支路电流 Ik与其各并联的电阻 Rk值成反比，即电阻 Rk值越大，则支路电流 Ik越小。

当 R1=R2=…=Rn=R 时，各支路电流相等，即 I1=I2=…=In，则支路电流 Ik为

【例1.17】 电路如图1.64（a）所示，试分别计算两种已知条件下的电流 I1、I2、I3、I和图1.64（b）等效电阻 R0，并画出测量1.64（a）电路中电压、电流的仪表符号接线电路图。

（1）已知电阻 R1=R2=R3=6Ω，电压US=12 V。

（2）已知电阻 R1=2Ω，R2=3Ω，R3=6Ω，电压US=12 V。(www.xing528.com)

图1.64　例1.17图

分析：

（1）并联电阻相等时，由式（1.17）得等效电阻由欧姆定律得支路电流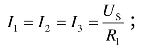由式（1.22）得总电流I=3I1。

（2）由式（1.16）得等效电阻 R0=R1// R2//R3；由式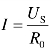得总电流；由式（1.20）得支路电流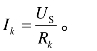

（3）测量电流时，电流表串联在支路中；测量电压时，电压表并联于电路的两点上。

解 （1） R1=R2=R3=6Ω，US=12 V。

等效电阻

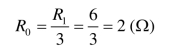
由欧姆定律得支路电流

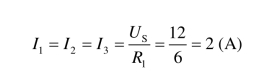
总电流为

因 R1=R2=R3，则图1.64（b）中等效电阻 R0为

（2） R1=2Ω，R2=3Ω，R3=6Ω，US=12 V。等效电阻

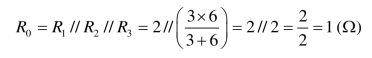
由欧姆定律得各支路电流

总电流为

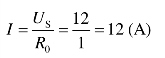
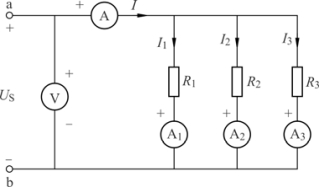
图1.65　电压、电流的测量接线电路图

（3）测量1.64（a）电路中电压、电流的接线电路，如图1.65 所示。

结论：并联支路的端电压相等，但各支路电流可有所不同（或相同），即并联电路具有分流功能。

4.电阻并联电路的功率

并联电阻电路（见图1.65）的总功率P 等于各个电阻 Rk消耗的功率 Pk之和，如式（1.13）所示，即

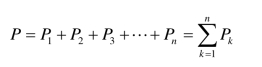
【例1.18】 试求例1.17 各元件消耗的功率及消耗的总功率，并验证功率平衡。已知电阻R1=2Ω，R2=3Ω，R3=6Ω，电压US=12 V。

分析：各电阻消耗的功率为Pk=IkUS；电路消耗的总功率为 PR=P1+P2+P3；电源提供的总功率为 PS=IUS；功率平衡为 PR-PS=0。

解　电阻 R1消耗功率为

电阻 R2消耗功率为

电阻 R3消耗功率为

电路消耗的总功率为

电源提供的总功率为

验证功率平衡

结论：电路的功率计算与电路的结构（串联或并联）无关，只与元件上的端电压Uk、电流 Ik有关，即 Pk=IkUk；功率的性质（是“提供”还是“消耗”功率）与电压Uk、电流 Ik之间的方向关系（是“关联”还是“非关联”方向）有关。当电压Uk与电流 Ik为关联方向时，Pk=IkUk﹥0为消耗功率，Pk=IkUk ﹤0为提供功率；当电压Uk与电流 Ik为非关联方向时，Pk=IkUk﹥0为提供功率，Pk=IkUk﹤0为消耗功率。