琥珀酸单薄荷酯的热重分析研究

图2-27为琥珀酸单薄荷酯在10.0 K·min-1升温速率下的热重（TG）和微商热重（DTG）图。从图中可以看出，在一定的升温速率下，随着温度的升高，琥珀酸单薄荷酯热裂解经历了三个不同的阶段。第一阶段为常温T0到T1，热重曲线几乎为一个平台，期间发生轻微的热失重。这是发生“玻璃化转变”现象的一个相变过程。第二个阶段是从T1到T3，此区域是琥珀酸单薄荷酯热失重的主要阶段。琥珀酸单薄荷酯分解生成小分子气体和大分子的可冷凝挥发成分而造成明显热失重，并在T2时其失重速率达到最大值。此阶段吸收的热量占整个反应的主要部分。第三个阶段为T3之后，由于琥珀酸单薄荷酯对热不稳定，总失重率达到100%，出现一个平台。

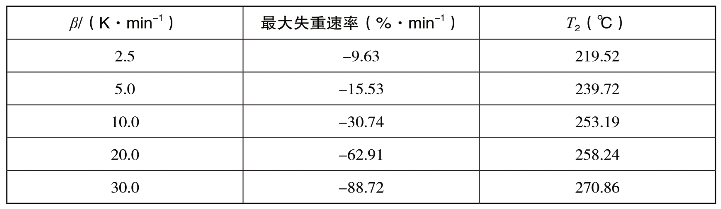
从图2-28中可以看出，琥珀酸单薄荷的TG与DTG曲线在2.5，5.0，10.0，20.0和30.0的不同升温速率下具有一致的变化趋势，即随着升温速率的增加，各个阶段的起始和终止温度向高温侧移动，且主反应区间也增加。这是因为达到相同温度，升温速率越高，试样经历的反应时间越短，从而反应程度越低。同时升温速率影响测点与试样、外层试样和内部试样间的传热温差和温度梯度，从而导致热滞后现象加重，致使曲线向高温侧移动。在不同升温速率下琥珀酸单薄荷酯达到最大热失重速率时的温度如表2-6所示。

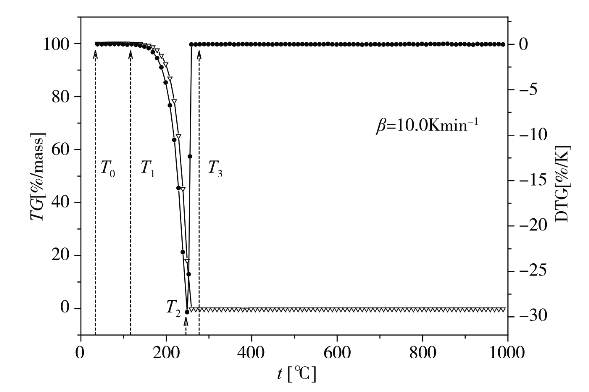
图2-27　琥珀酸单薄荷酯的热失重过程

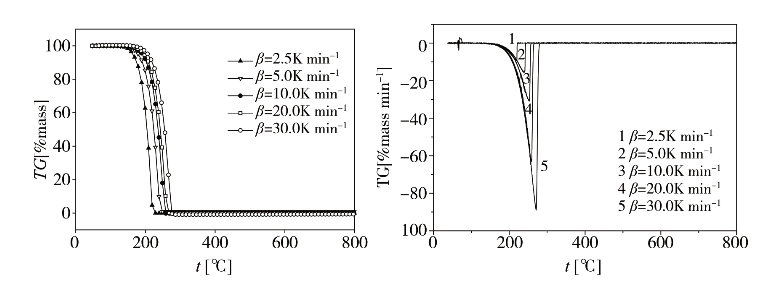
图2-28　不同升温速率下琥珀酸单薄荷酯的TG和DTG曲线

表2-6　不同升温速率下琥珀酸单薄荷酯达到最大热失重速率时的温度

（2）热分解动力学模型和动力学参数的确定

使用热重法对琥珀酸单薄荷酯主反应区进行分析，求得其动力学参数，从而建立该区间的表观反应动力学模型。对于一个非等温热分解动力学，最常使用如下的动力学方程:(www.xing528.com)

在此研究中，使用公式（2-4）所示的简单动力学方程来模拟琥珀酸单薄荷酯的热失重现象，其中α为相对失重或称转化率，定义为α=(m0−mτ)/(m0−m∞)。m为样品质量，m0和m∞分别代表反应初始和终止时的样品质量。

速率常数k由Arrhenius公式k=Aexp(−Ea/RT)求得，指数前因子A和活化能Ea的表达式由热重曲线的分析计算求得。机理函数f(α)的表达式通常假设为f(α)=(1−α)n，用以描述反应模式。n为反应级数，结合公式（2-4）并引入升温速率与反应时间的线性关系，即β=dT/dt，可得到公式（2-5）

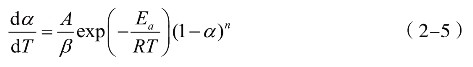
将公式（2-5）取对数后差分得到公式（2-6）:

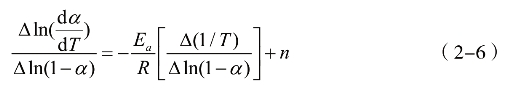
公式（2-6）左边与(1/)T∆呈线性关系，由直线斜率可求得活化能Ea，再根据公式（2-4）和Arrhenius公式及()fα可计算出指数前因子A。公式（2-6）即为琥珀酸单薄荷酯主反应区热失重过程的动力学模型。计算出相应的动力学参数如表2-7所示。

表2-7　琥珀酸单薄荷酯在不同升温速率下的动力学参数

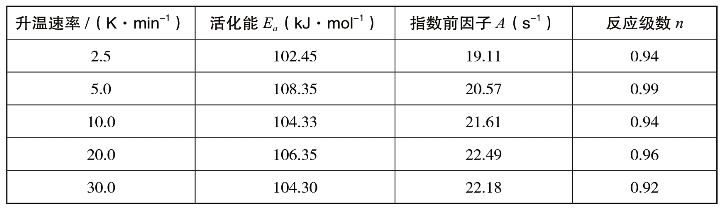
从表2-7中可以看出，不同升温速率下的活化能差异不大，证实了主反应区的热失重是简单级数反应。