稳态液动力及其在液压阀中的作用

液动力是指液压阀内的压力介质对阀芯，由于流动而引起的附加作用力。稳态液动力则是指在没有时变流动的情况下的液动力。要强调的是：

1）当容腔内的液体有流动时，就会出现如伯努利方程所描述的“速度低处压力高，速度高处压力低”的现象。如果还是按帕斯卡定律，“压力处处相等”的方式去计算液体对容器壁面的作用力，就必须加上一个修正量。这个修正量就是稳态液动力的来源和本质。稳态液动力不是一个可以独立存在的力，它仅仅是一个修正量而已。从这个本质出发，也许我们不能定量地计算出液动力，但至少不会犯方向性的错误。

2）当液体流动时，如果可以得到所研究的壁面附近液体速度的数学表达式，再能够根据描述压力（压能）和速度（动能）互相转换的伯努利方程，写出压力分布的数学表达式的话，则理论上有可能用积分的方法求出液体对固体壁面的作用力，扣除静压部分，就可得到稳态液动力。

但是，由于流体的运动常常很复杂，速度、压力实际分布状态的精确数学表达式一般都无法得到，导致难于通过积分来求解稳态液动力。现在，已经有了一些尝试，利用流场仿真（CFD）的方法，直接计算液体对固体壁面的作用力。

3）运用取控制体，计算动量改变的方法，可以避免寻找壁面压力分布数学式的困难，有时不失为一条捷径。但这是有条件的，并非处处可行的。其中，很重要的一条就是：在取控制体，利用动量法来研究某一方向上阀芯所受到的液动力时，该方向上作用于控制体壁面的其他影响力必须可计算，或能可信地忽略。忽视了这一点，就可能引出错误的结论。

下面对滑阀和锥阀分别作一些讨论。

1.滑阀

（1）具有完整阀腔的滑阀

对于具有完整阀腔的滑阀（见图1-45），设液体对阀芯的环形作用面积为A，液体压力为p。

图1-45 具有完整阀腔的滑阀（无流动）

1）在无流动时，液体对阀芯的作用力F₁=F₂=pA。完全平衡，合力为零。

2）在液体流动时，液体对阀芯的作用力分布如图1-46所示。

在截面1-1处，液体基本保持静止（有少量涡流），因此压力基本保持处处相等，F₁=pA。

在截面2-2处，由于流速不同，压力也不同。越是靠近开口处，流速越高，压力就越低。

因此，F₂＜F₁。合力的方向向右，倾向于使阀口关闭。

当然，图1-46中截面2-2的压力分布被画成了线性的，只是示意性的，为了作图简便，并非实际状况。如真是那么有规律，就很容易计算出来了，下同。感兴趣者请看所附光盘中，利用流场仿真（CFD）做出的彩图。

3）控制体-动量法。取圆筒形控制体，如图1-47灰色部分所示。

图1-46 具有完整阀腔的滑阀（有流动时）

液体进入控制体时，开口小，流速v₂很高，其轴向分量为v₂cosα₂。所以，若设液体密度为ρ，进入控制体的流量为q_V，则在单位时间里液体进入控制体时所具有的动量的轴向分量为ρq_Vv₂cosα₂。

液体流出控制体时，开口大，流速v₁很低，几乎无轴向分量。所以，其动量的轴向分量可以近似为零。

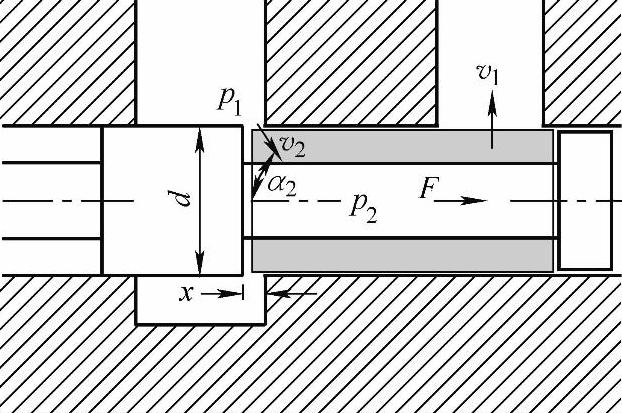
图1-47 具有完整阀腔的滑阀的控制体

因为，如果忽略阀体对液体的摩擦力的话，那么，除阀芯外就没有其他界面对液体有轴向作用力，所以可以认为，动量的变化ρq_Vv₂cosα₂全部作用在阀芯上了。

在无流动时，液体对阀芯的合力为零。有流动时，有一个向右的作用力。所以，可以称此力为液动力

F_y=ρq_Vv₂cosα₂ （1-2）

流速为

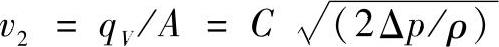
式中 A——开口面积；

∆p=p₁-p₂——开口两边的压差；

C——流量系数。

所以，液动力也可写作

式中系数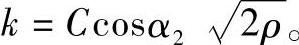

即，液动力与通过开口的流量及两端压差的平方根成正比。

要指出的是：

1）在阀开口附近，高速液体引起的涡流和气蚀也会把部分动能转化为热能，而且也没有考虑阀体对流体的轴向摩擦力，因此，用动量变化的方法计算出来的力，总是大于直接从阀芯上测量出来的力。

2）射流角的大小取决于配合间隙及开口的大小。据说，在完全理想情况下计算出来为69°。但实际情况较为复杂，并非一定是69°。

3）如果流动方向相反，会得到同样的结果：液动力向右，趋于使阀口关闭。

4）液动力是限制电磁换向阀工作范围的最主要因素。如果改变阀芯形状，使出流速度v₁也具有向右的轴向分量，那就可减小作用在阀芯上的液动力（见图1-48）。在这方面已有不少研究成果。

图1-48 减小液动力的措施（IFAS）

（2）具有不完整阀腔的滑阀（图1-49）

1）如果阀腔内的压力为p，且没有流动，则液体对阀芯的作用力F为pA，方向向左，趋于使阀口开启。这是静压力所致。因为并非流动所致，所以不是液动力。

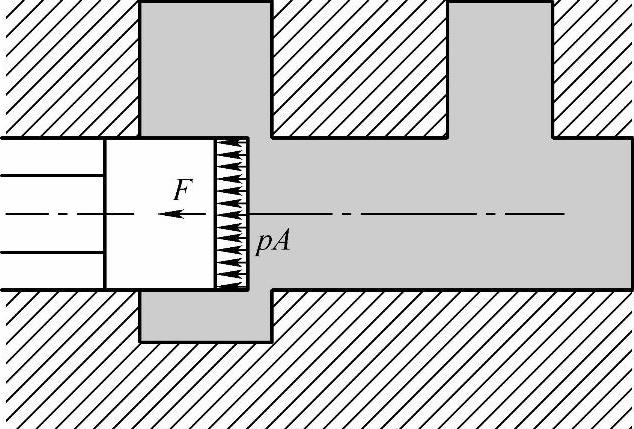
图1-49 无流动时对阀芯的静压力分布

2）如果有流动（见图1-50），则液体对阀芯的作用力F方向还是向左，但小于pA，因为近阀口处的压力由于流动，低于静压力p。如果还是按pA计算，就必须加上一个修正量F_y，即

F=pA+F_y

这个F_y就是液动力，方向向右，也是趋于使阀口关闭。F_y不能直接测出来。F可以测得，减去pA，才是液动力F_y。

如果通过求控制体动量变化的途径估算F_y，其数值会与阀腔完整时相同。

（3）液动力在系统中的表现 以上是单独考察液动力在滑阀开口处的状况。在一个完整的液压系统中，阀开口两边的压差、通过的流量和开口大小之间有一定的依存关系。

图1-50 有流动时阀腔内的压力分布

1）液动力与开口的关系。如果把液体进入控制体的开口近似地看为一通流面积为πxd的圆环（见图1-47），就有

q_V=v₂πxd （1-4）

所以

v₂=q_V/πxd （1-5）

从式（1-2）、式（1-5）就可推出液动力

F_y=ρq²_Vcosα₂/πxd=k₁q²_V/x （1-6）

其中，k₁为含ρ、cosα₂、π、d等常数的一个系数。此式表明，如果流量不变，液动力与开口大小x成反比。

假定通过该开口的流量接近薄刃口的情况(www.xing528.com)

其中，C为流量系数。

将式（1-7）代入式（1-6）就可得

F_y=k₂x∆p （1-8）

其中，k₂为含ρ、cosα₂、π、C、d等常数的一个系数。此式表明，如果开口两边的压差不变，液动力与开口大小x成正比。

2）简化的液压系统。液压系统一般都可简化成图1-51，油源由一定量泵加一溢流阀组成。

3）当滑阀开口很小时（见图1-52区域I），泵排出的部分液体通过溢流阀溢出，系统工作在恒压工况，阀口压力p_P近似为溢流阀的设定压力p_s。此时：

① 通过阀口的流量q_V随开口x增加而增加。通过溢流阀的流量q_V1随开口x增加而减少。

② 因为压差∆p=p_P-p₂基本保持不变，根据式（1-8），液动力F_y大致与开口x成正比。

图1-51 液压系统示意图

4）当滑阀开口大到一定程度后（见图1-52区域Ⅱ），泵排出的液体不再通过溢流阀溢出，系统工作在恒流量工况。此时：

① 阀口压力p_P随开口增大而减小。

② 通过阀开口的流量q_V基本保持不变，因此流速随开口增大而减小。根据式（1-6），液动力F_y与开口x大致成反比。

在区域I和Ⅱ的交界处，阀口压力p_P基本还在最高，通过阀的流量q_V也达到最大时，稳态液动力F_y达到最大值。

图1-52 压力流量及稳态液动力随开口的变化

液动力在液压系统中随阀开口变化如图1-46所示意的这种关系对其他形式的阀也是存在的（参见图1-59）。

表1-2列出了一些在给定压差和开口时的通过流量、液动力和液动压力的理论估算值（参见附录B），供读者有一感性认识。（油液密度ρ取860kg/m³，流量系数取0.6，射流角按69°计算）

表1-2 在给定压差和开口时的通过流量与液动力的理论估算值

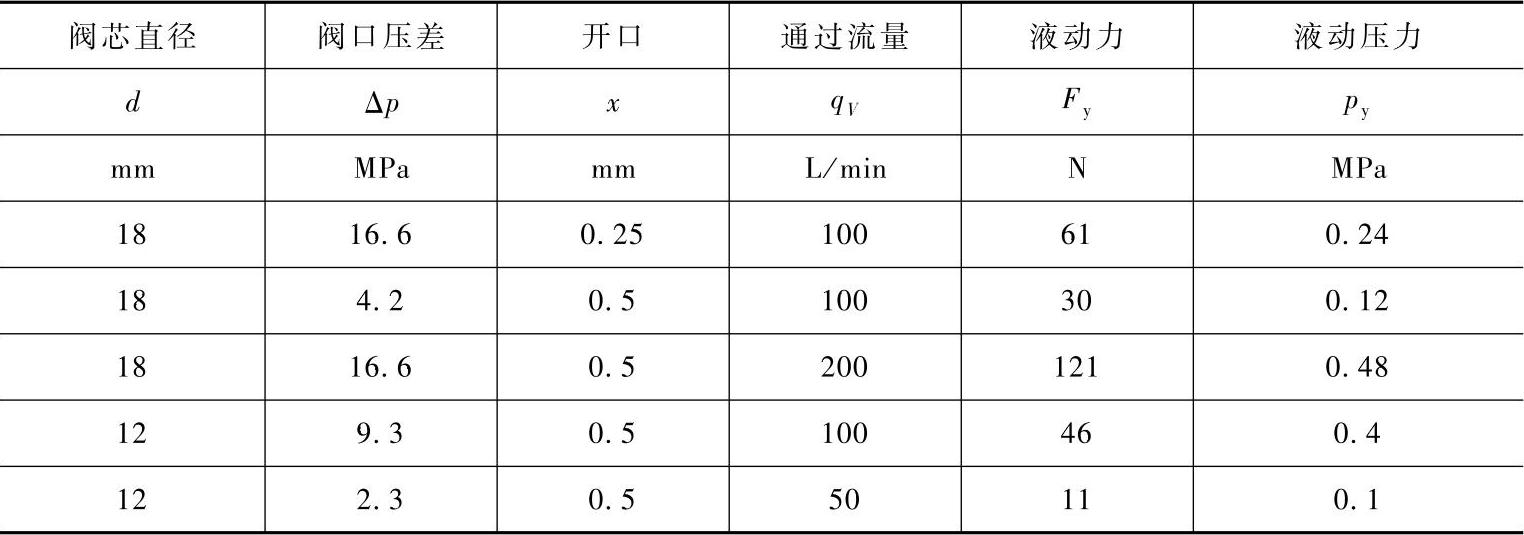
注：液动压力=液动力/阀芯端面面积。

2.座阀

座阀的情况较滑阀情况复杂得多，这是因为座阀有很多种变型，控制体也不那么容易取。以下以锥阀为例，作一说明。

（1）锥阀阀尖区

1）在液体无流动时（见图1-53），阀芯在阀尖区实际受到的压力分布如图1-53b所示。

图1-53锥阀（无流动时）阀尖区受到的静压力

a）阀尖区 b）压力分布

阀芯受到的轴向合力F=pA。因为没有流动，所以与液动力无关。

2）在液体流动时（见图1-54a），不管往哪个方向流动，阀芯实际受到的压力就不再处处相等。此时，越接近阀口处，流速越高，从而压力越低。图1-54b示意性地画出了锥阀在阀尖区所受到的压力分布。图1-54c示意性地画出了这些压力的轴向合力。

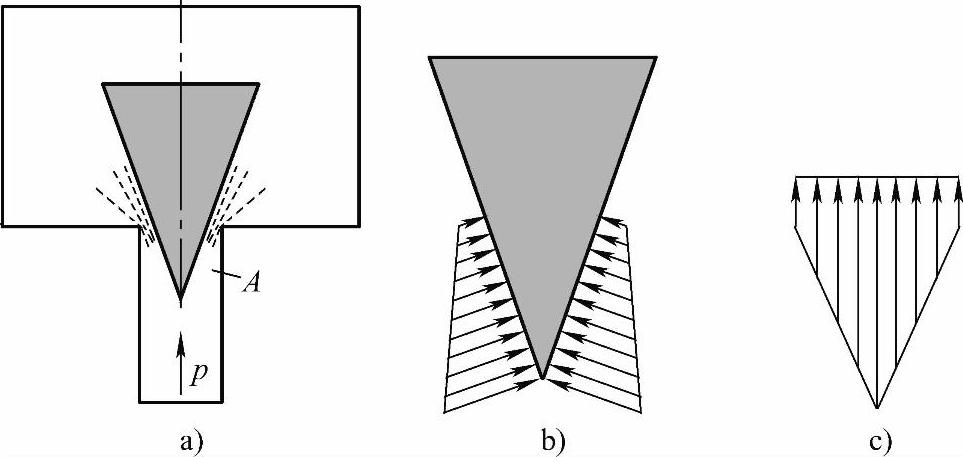
图1-54 锥阀（液体流动时）阀尖区受到的液压力

a）阀尖区 b）压力分布 c）轴向合力

如果阀芯实际受到的轴向合力F如果还是按静压力pA（见图1-55b）计算，就必须加上一个修正量，也就是液动力F_y（见图1-55c），方向向下，趋于使阀口关闭。

F=pA+Fy

（2）锥阀阀体区

1）液体无流动时（见图1-56），阀芯在阀体区实际受到的压力分布如图1-56b所示。

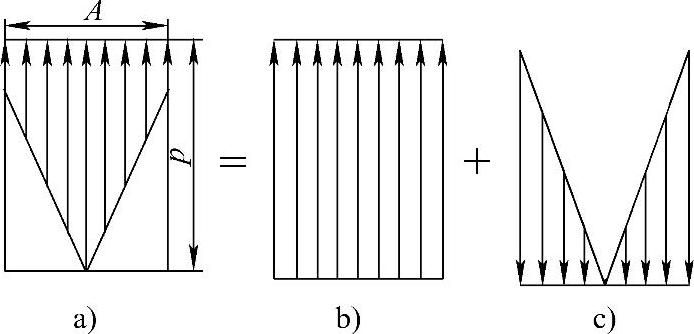
图1-55 阀芯受到的轴向力

a）轴向合力 b）静压力 c）液动力

轴向合力（见图1-56c）F=pA。因为无流动，所以与液动力无关。

在液体流动时（见图1-57a），不管往哪个方向流动，阀芯实际受到的压力就不再处处相等。此时，越接近阀口处，流速越高，从而压力越低。图1-57b示意性地画出了锥阀在阀体区所受到的压力。图1-57c示意性地画出了其轴向合力。

如果这个轴向合力F还是按静压力pA（见图1-58b）计算，就必须加上一个修正量，也就是液动力F_y（见图1-58c），方向向下，也是趋于使阀口关闭。

F=pA+F_y

锥形阀芯和锥形阀座在液压技术中应用得很多，特别是在盖板式二通插装阀中，其形式也多种多样。其液动力的确定要比滑阀复杂，其控制体的取法也随座阀的形式而变。

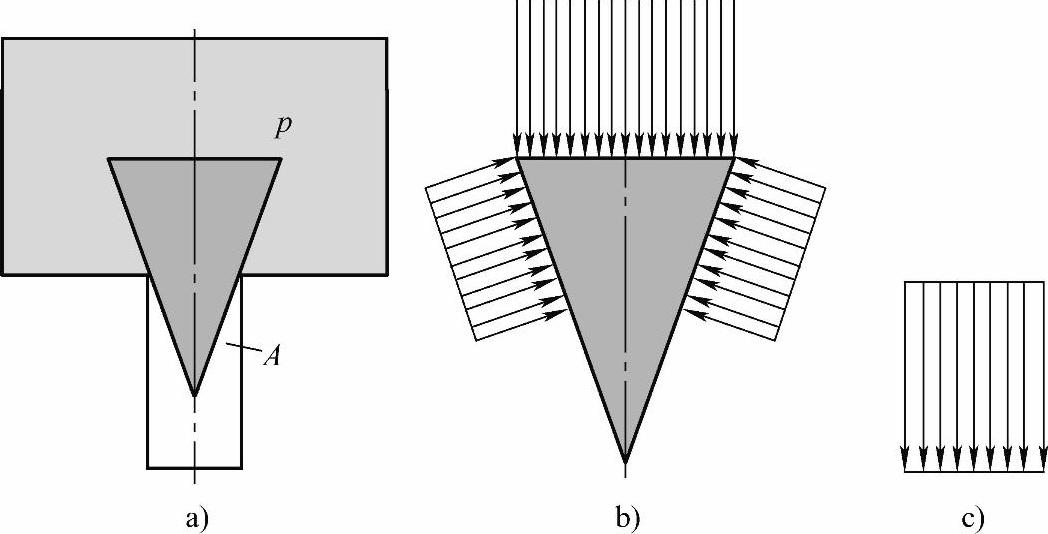
图1-56 锥阀（无流动时）阀体区受到的静压力

a）阀体区 b）压力分布 c）轴向合力

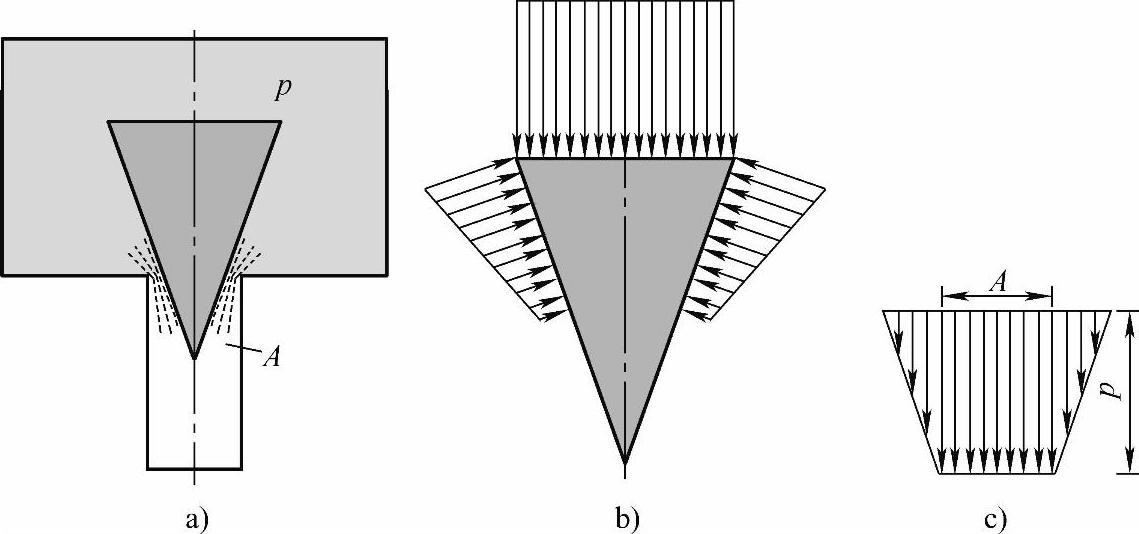
图1-57 锥阀，有流动时，阀体区受到的液压力

a）阀体区 b）压力分布 c）轴向合力

图1-58 阀芯受到的轴向合力

a）轴向合力 b）静压力 c）液动力

路甬祥教授在他的博士论文中对多种不同形式的滑锥阀的稳态液动力随开口的变化做了认真详尽的研究，把理论计算与实测作了对比后指出，用动量变化算出的液动力往往大于实测。在他与胡大綋教授合编著的《电液比例控制技术》中对此作了介绍。这里摘录其中两张图供读者参考（见图1-59）。

总的来说，液动力总是趋于使阀口关闭的方向。

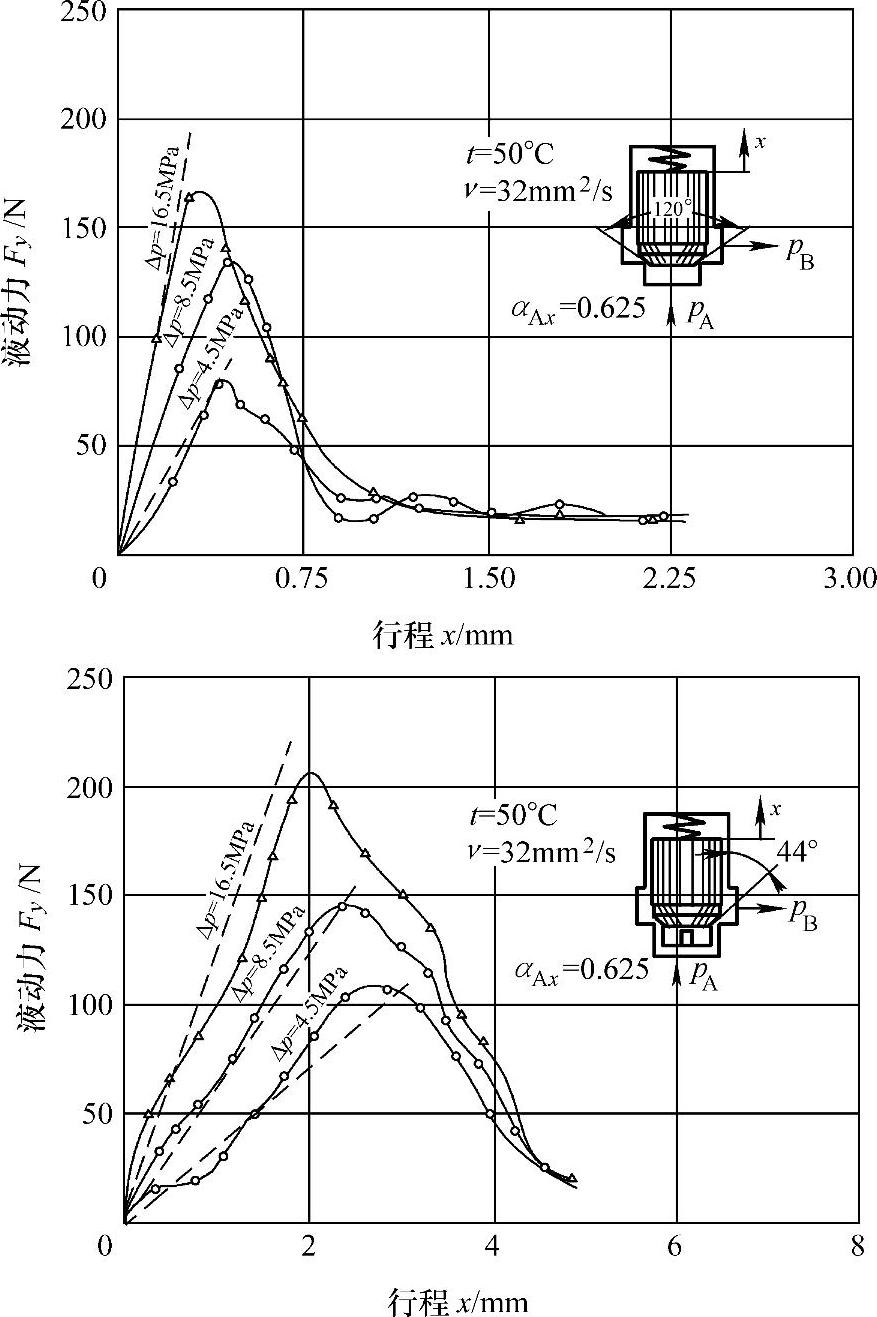
图1-59 NG20二通插装阀的液动力曲线

——实测 ------理论计算

如果流动是时变的话，液动力也会随之变化，即还有所谓瞬态液动力。这里就不展开讨论了。