圆柱与圆锥的相贯线投影及分析

【例2-20】 补全圆柱相贯的正面投影，如图2-20（题）所示。

图2-20 （题）

图2-20 （解）

【解】 根据所给投影，判断相贯在一起的立体为圆柱筒和半圆柱筒，两立体轴线垂直相交，所求的相贯线分别为外表面与外表面相贯线和内表面与内表面相贯线，并且两圆柱外表面直径相同，因此相贯线投影为直线。

作图步骤略，结果如图2-20（解）所示，立体图如图2-20（立体）所示。

图2-20 （立体）

【例2-21】 补画正面投影中漏画的相贯线，如图2-21（题）所示。

图2-21 （题）

图2-21 （解）

【解】 水平放置的半圆柱上开有同轴的半圆柱孔，同时在与轴线垂直相交的铅垂方向上（竖放）开有完整的圆柱孔。由于圆柱（孔）的积聚性，本题相贯线的水平投影和侧面投影均在圆或圆弧上，只需求出正面投影即可。要注意的是，横放圆柱的外圆柱面和内圆柱面与竖放圆柱孔均有相贯线。

作图步骤略，结果如图2-21（解）所示，立体图如图2-21（立体）所示。

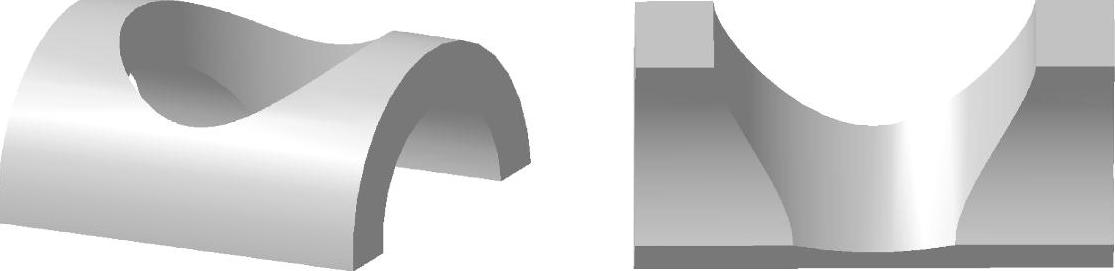
图2-21 （立体）

【例2-22】 补画圆柱与圆锥的相贯线投影，如图2-22（题）所示。

【解】 分析及作图步骤略，结果如图2-22（解）所示，立体图如图2-22（立体）所示。

图2-22 （题）

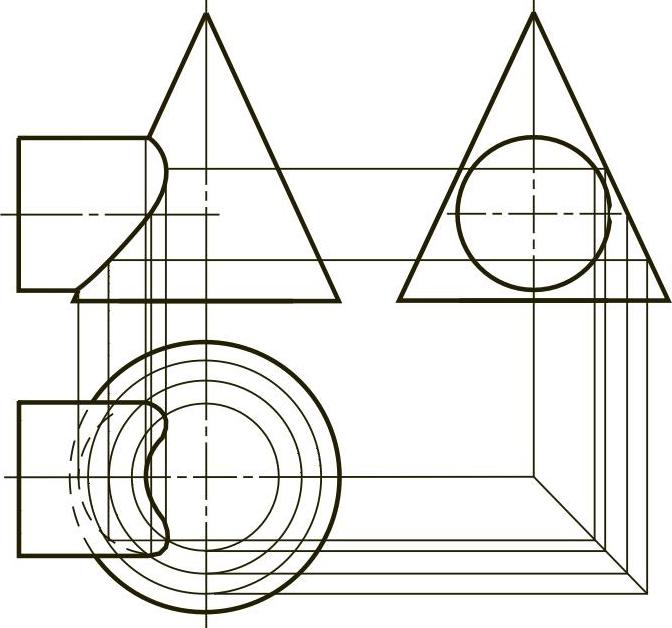
图2-22 （解）

图2-22 （立体）

【例2-23】 补画圆柱的侧面投影，如图2-23（题）所示。

图2-23 （题）

图2-23 （解）

【解】 分析及作图步骤略，结果如图2-23（解）所示，立体图如图2-23（立体）所示。

图2-23 （立体）

【例2-24】 补画圆锥钻孔后的正面投影，如图2-24（题）所示。

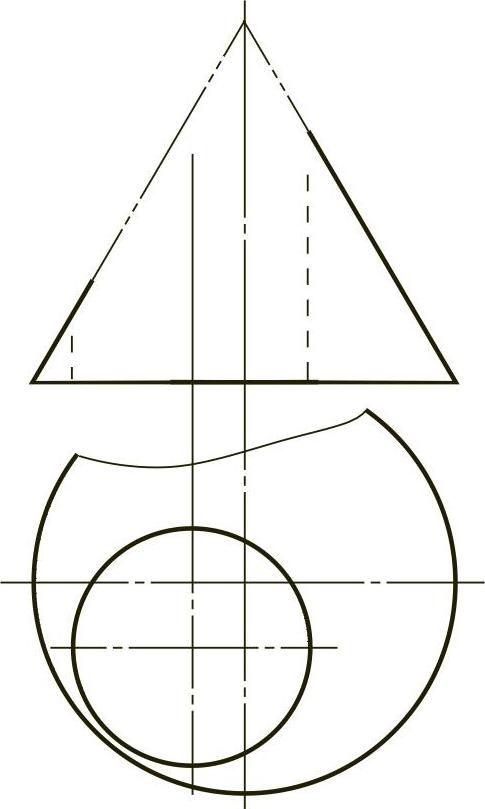
图2-24 （题）

图2-24 （解）

【解】 在轴线铅垂的圆锥面上钻一个轴线铅垂的圆柱孔（不同轴），要求的相贯线即为圆柱孔的内表面与圆锥的外表面之间的交线。由于圆柱孔的内表面具有积聚性，相贯线的水平投影就是孔的水平投影圆，利用锥面取点的方法可求出相贯线的正面投影。(www.xing528.com)

作图步骤略，结果如图2-24（解）所示，立体图如图2-24（立体）所示。

【例2-25】 补画相交圆柱的正面投影，如图2-25（题）所示。

【解】 分析及作图步骤略，结果如图2-25（解）所示，立体图如图2-25（立体）所示。

【例2-26】 求半圆柱筒的正面投影，如图2-26（题）所示。

图2-24 （立体）

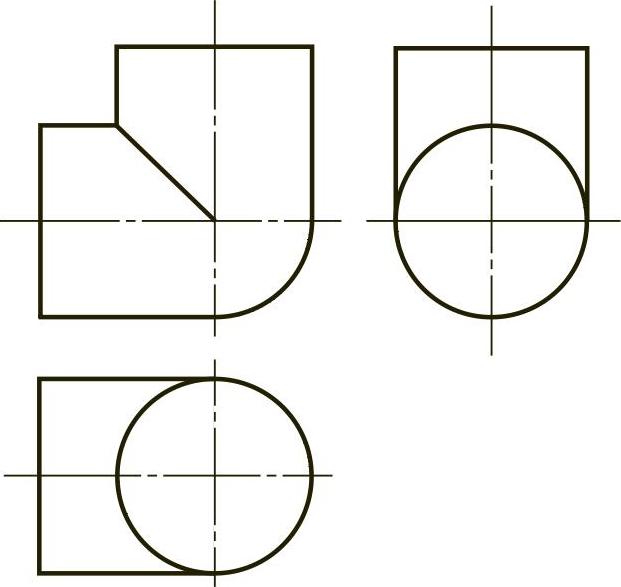
图2-25 （题）

图2-25 （解）

图2-25 （立体）

图2-26 （题）

图2-26 （解）

【解】 分析：本题主要要求正面投影中的相贯线，相贯线有两条，分别是长圆孔内表面与圆柱筒外表面，以及长圆孔内表面与圆柱筒内表面之间的相贯线。

作图步骤略，结果如图2-26（解）所示，立体图如图2-26（立体）所示。

图2-26 （立体）

【例2-27】 补画相贯在一起的三个立体的正面投影，如图2-27（题）所示。

图2-27 （题）

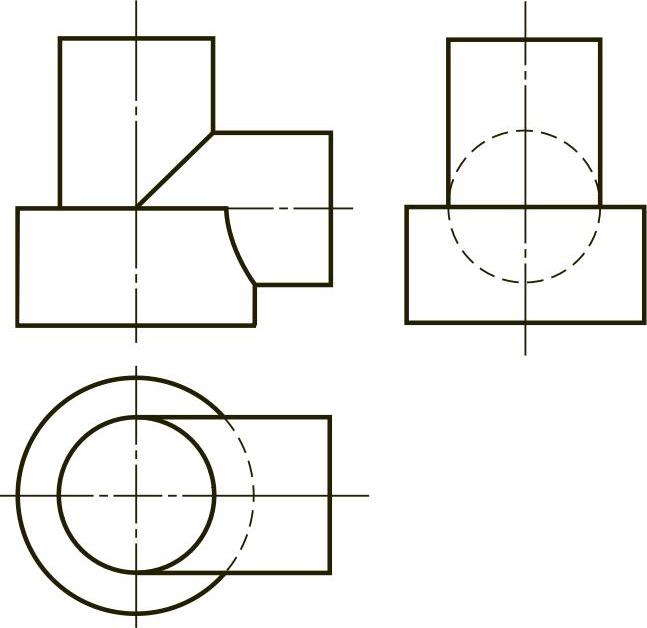
图2-27 （解）

【解】 分析：本题中三个圆柱相贯在一起，其中两个中心线竖直放置的圆柱之间不存在相贯线，要求的相贯线是水平放置的圆柱分别与其他两个圆柱之间相交所产生的相贯线。由于圆柱表面具有积聚性，因此这两段相贯线在水平面和侧面的投影分别与圆柱面的投影相重合。根据水平投影，竖直放置的上面的圆柱与水平圆柱的直径相同，因此这两个圆柱之间的相贯线的正面投影为一条直线；水平圆柱与下面的圆柱之间的相贯线可以通过积聚性表面取点的方法求得。

作图过程略，结果如图2-27（解）所示，立体图如图2-27（立体）所示。

【例2-28】 补画相贯在一起的立体的相贯线，如图2-28（题）所示。

【解】 分析：本题中相贯在一起的三个立体分别是：轴线竖直的圆柱、轴线水平的圆锥台和圆柱上方的半圆球。圆柱与圆锥的轴线均通过球心，且前后对称。由于圆柱和圆球的直径相同，所以它们的相交不产生相贯线。圆锥轴线通过球心，它们之间的相贯线为侧平圆，侧面投影反映实形，水平投影为铅垂方向线。由于积聚性，圆锥与圆柱表面交线的水平投影是已知的，且不可见，因此，可用在圆锥表面取点的方法求出交线上若干个点的正面和侧面投影。两段交线的分界点分别位于圆锥的最前和最后的轮廓线上。

作图过程略，结果如图2-28（解）所示，立体图如图2-28（立体）所示。

图2-27 （立体）

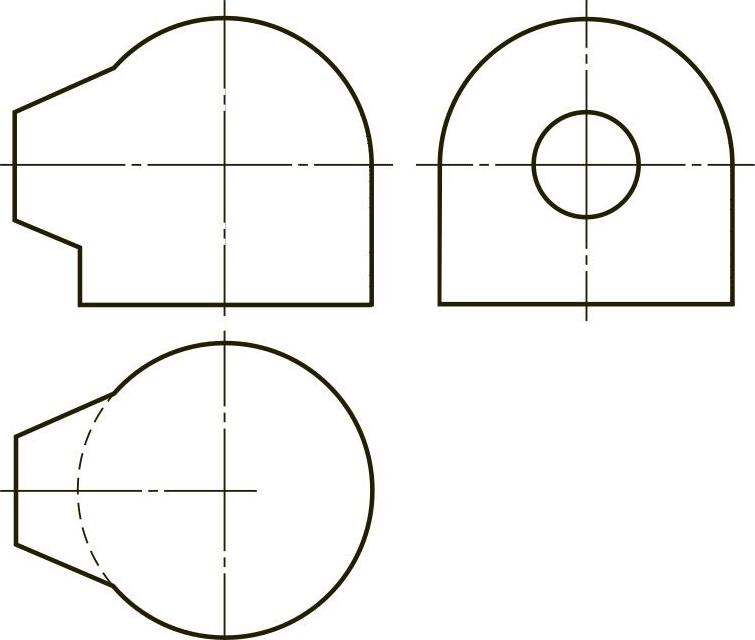
图2-28 （题）

图2-28 （解）

图2-28 （立体）