如何求解三角形平面ABC与V面的夹角和点D到平面三角形ABC的距离及投影

【例1-28】 求点D到平面三角形ABC的距离及投影，如图1-28（题）所示。

【解】 1.分析

求点到平面的距离可以转化为点到直线的距离，通过把平面转化为投影面垂直面得到其积聚性投影，然后过点作积聚性投影的垂线，返回即得。

2.步骤

1）经一次换面得到投影面垂直面a₁′b₁′c₁′，同时得到d₁′。

2）过d₁′点作a₁′b₁′c₁′的垂线，垂足k₁′，则d₁′k₁′即为所求距离实长。

3）返回d₁′k₁′，即得实长投影，结果如图1-28（解）所示。

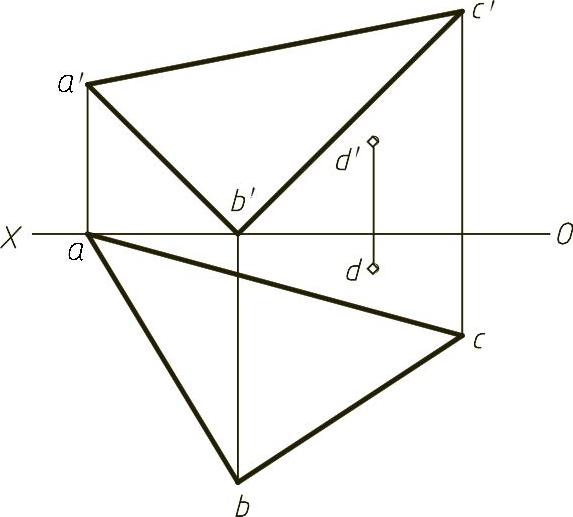
图1-28 （题）

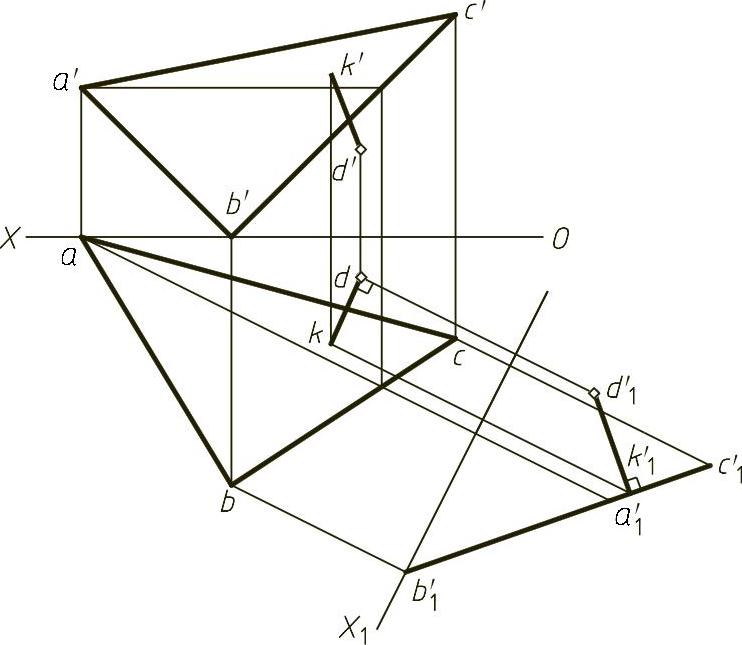
图1-28 （解）

【例1-29】 求三角形平面ABC与V面的夹角β，并在该平面上作一条AD线，且AD长为30mm，并交BC于D，如图1-29（题）所示。(www.xing528.com)

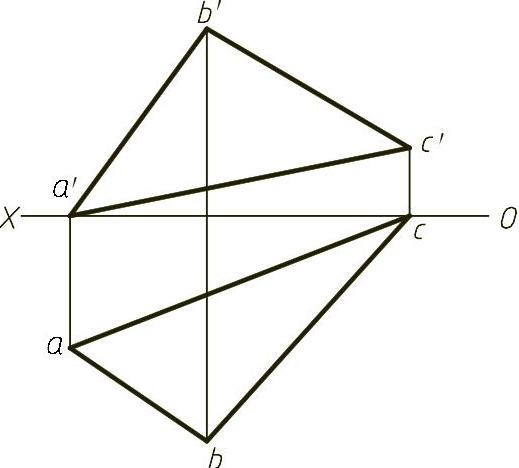
图1-29 （题）

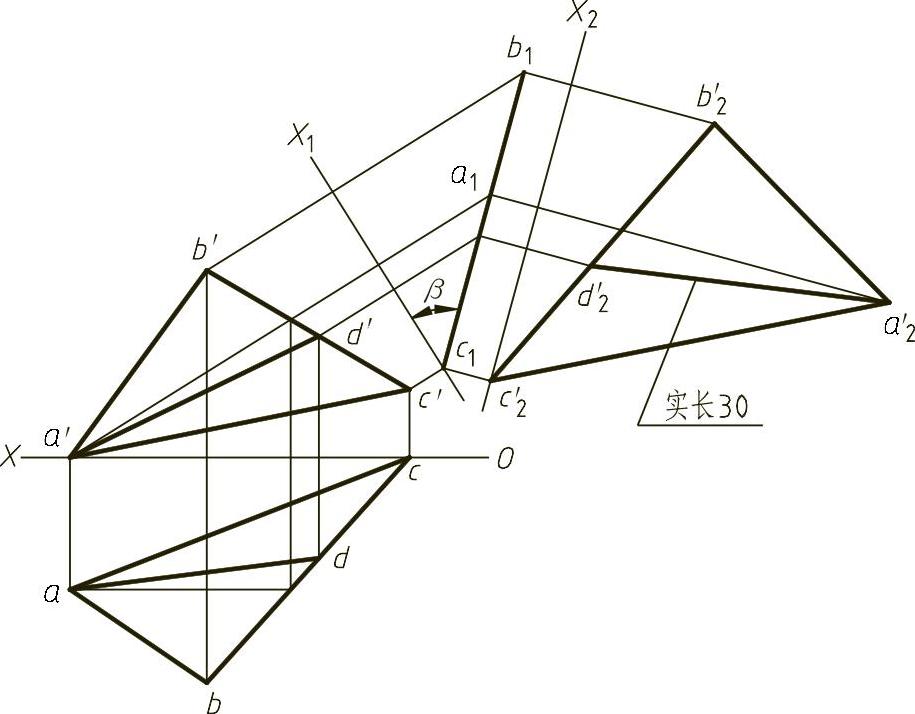
图1-29 （解）

【解】 1.分析

求平面与V面夹角，只需将△ABC变换为H面的垂直面；求AD的实长，只需在第一次变换的基础上将三角形平面变换为实形，以A点为圆心，30mm为半径作圆，与BC的交点即为D，返回即得。

2.步骤

1）首先更换H面，得到△ABC在H1面上的投影a₁b₁c₁，则a₁b₁c₁与O₁X₁轴的夹角即为β角。

2）再更换V面，得到a₂′b₂′c₂′，即为实形。

3）以a₂′点为圆心，以30mm为半径作圆，交b₂′c₂′于d₂′，连接a₂′d₂′，返回即得所求AD，结果如图1-29（解）所示（本题有两解）。