如何做出三角形ABC的水平投影及可见性判断

【例1-20】 已知△ABC∥EDFG（DE∥FG），求作△ABC的水平投影，如图1-20（题）所示。

【解】 本题主要考查面与面平行的几何条件。根据几何条件，分别在两个平面内构造两条相交直线，与另一平面内的两条相交直线相互平行，则两平面平行。由题目，AB与DE已经相互平行，再在EDFG平面内构造一条与BC相互平行的直线GI，据此作出BC的水平投影，即可作出△ABC的水平投影，如图1-20（解）所示。

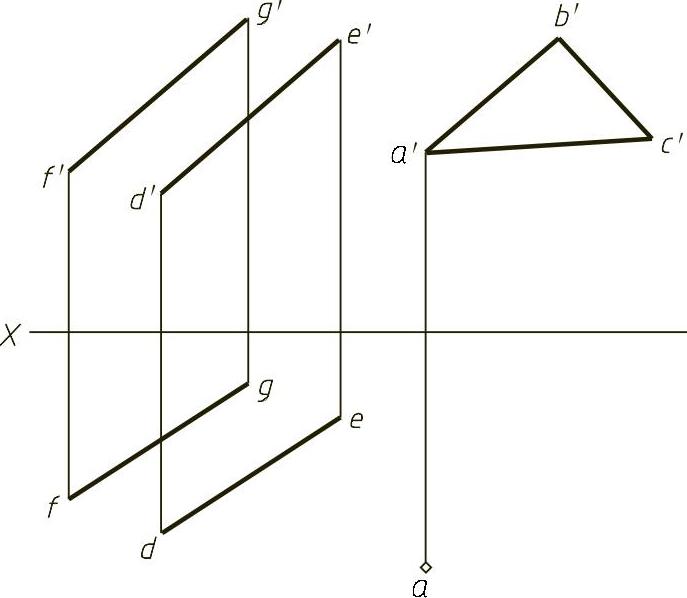
图1-20 （题）

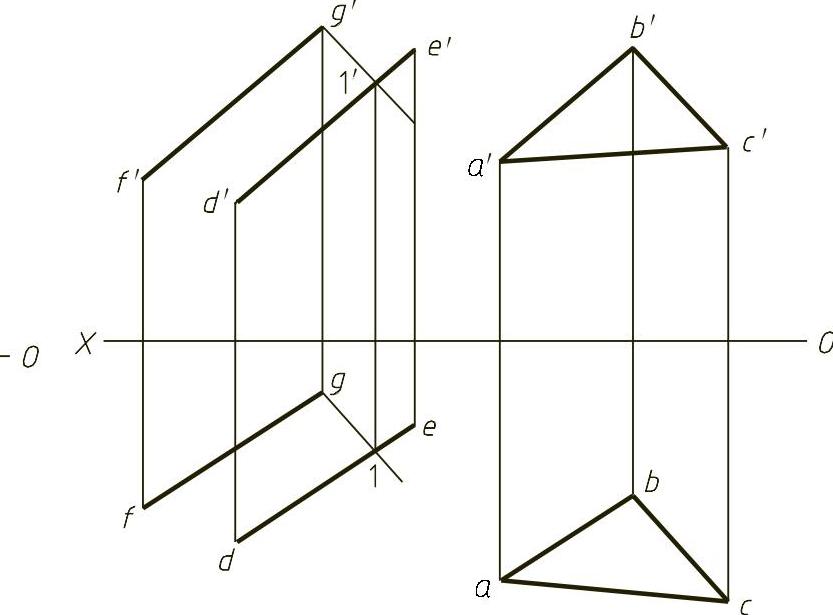
图1-20 （解）

【例1-21】 求直线MN与平面的交点，并判别可见性，如图1-21（题）所示。

【解】 本题主要考查特殊位置直线与一般位置平面相交求交点。本题中，MN直线为正垂线，因此要求的交点的正面投影与直线的正面的积聚性投影重合在一起，交点的水平投影采用平面上取点的方法，通过添加通过k′的辅助直线c′1′，在c1上得到k，求解结果如图1-21（解）所示。

【例1-22】 求直线MN与平面ABC的交点K，并判别可见性，如图1-22（题）所示。

【解】 本题主要考查一般位置直线与特殊位置平面相交求交点。本题中平面ABC为正垂面，在正面积聚为一条直线，积聚性投影a′b′c′与m′n′的交点即为要求交点的正面投影k′，向下作投影线可以找到在mn上的k点。在判断可见性的时候，通过找到一组重影点ⅠⅡ来进行判断，如图1-22（解）所示。

【例1-23】 求两平面的交线，如图1-23（题）所示。

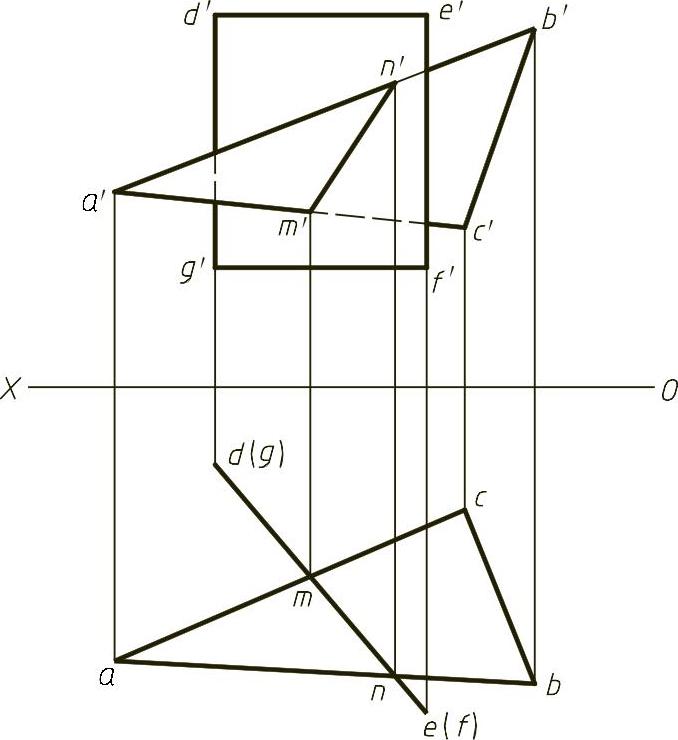
【解】 本题主要考查一般位置平面与特殊位置平面相交求交线。题目中DEFG平面为铅垂面，其水平面积聚性投影在abc内部的一段为两平面的交线mn，分别过m点和n点向上作投影线，可以找到在a′b′和a′c′上的n′、m′，连接即为交线的正面投影，然后可以通过重影点判断可见性，结果如图1-23（解）所示。

【例1-24】 求两平面的交线，如图1-24（题）所示。

【解】 本题主要考查两特殊位置平面相交求交线。题目中平面ABC和平面DEFG为铅垂面，它们水平面积聚性投影的交点即为交线的积聚性投影，交线为一条铅垂线。过交线的水平投影向上作投影线，可以找到交线的正面投影，然后可以通过重影点判断可见性，结果如图1-24（解）所示。

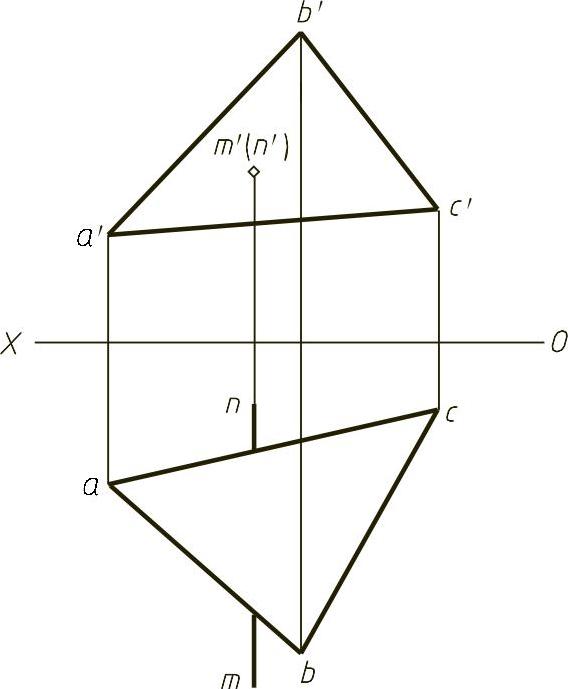
图1-21 （题）

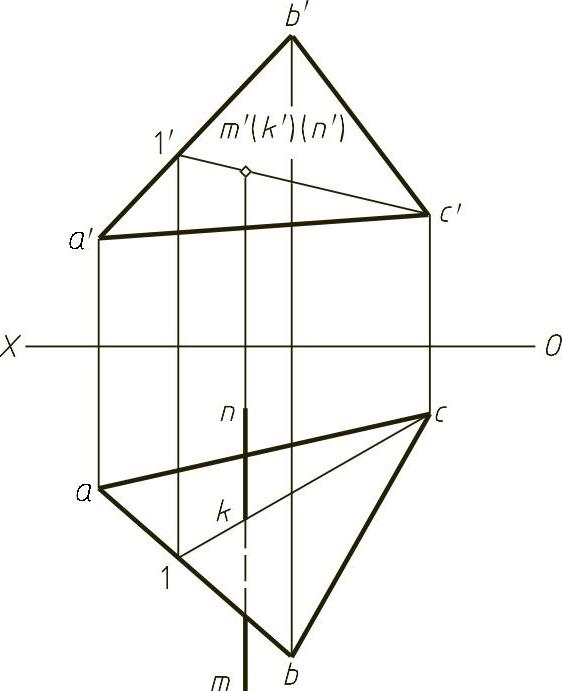
图1-21 （解）

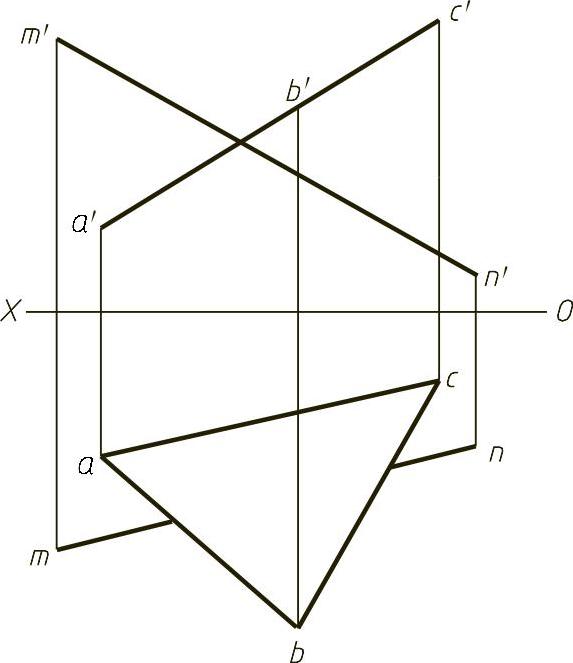
图1-22 （题）

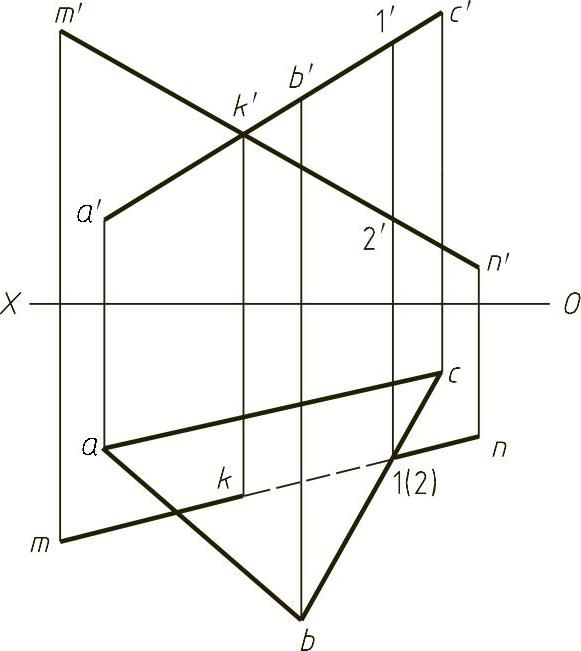
图1-22 （解）

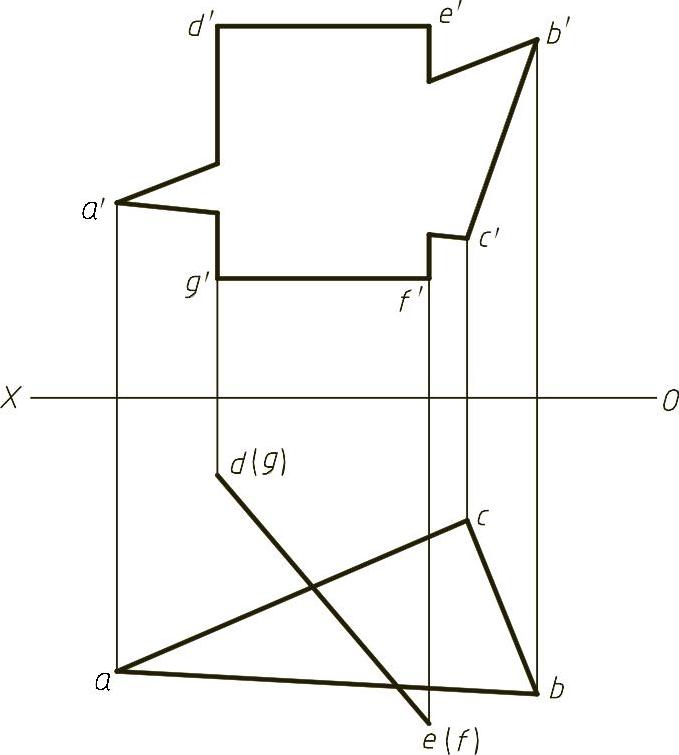
图1-23 （题）

(www.xing528.com)

图1-23 （解）

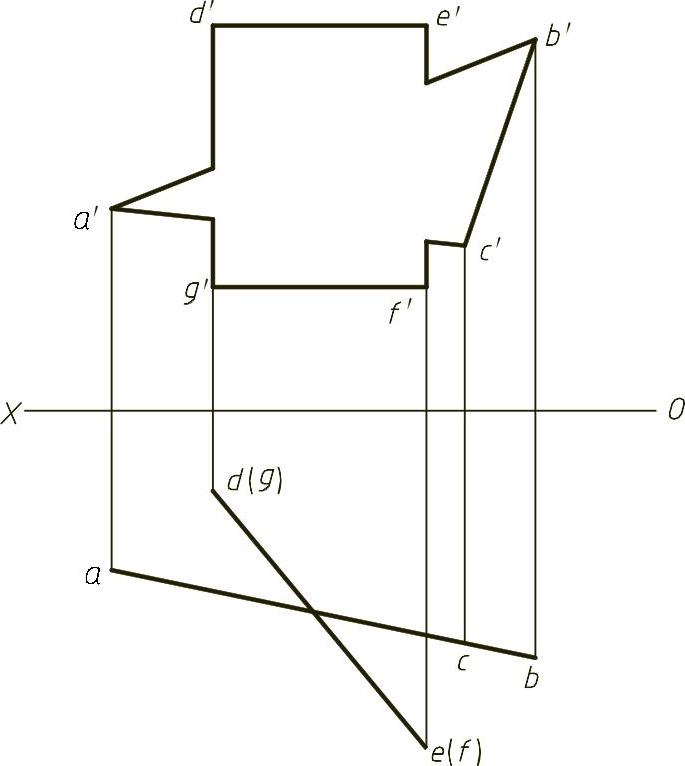
图1-24 （题）

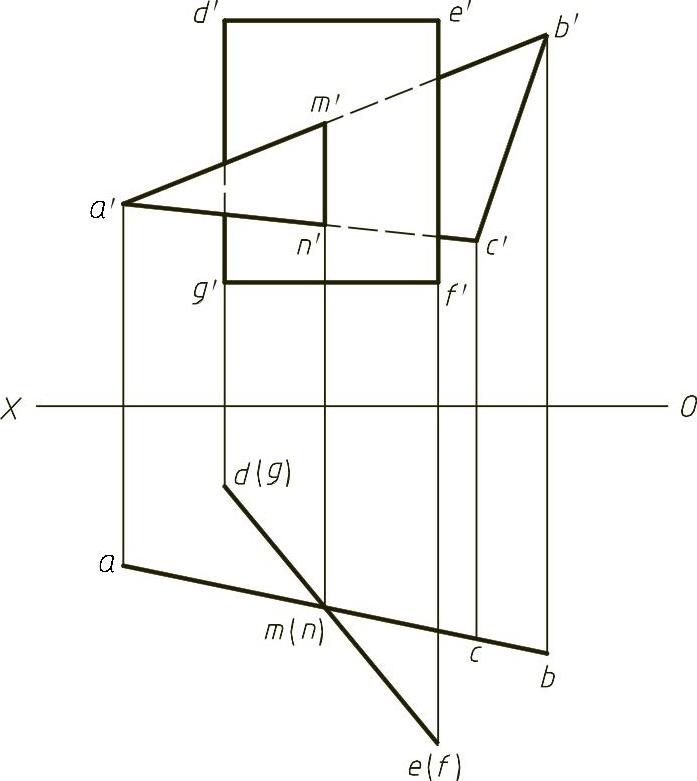
图1-24 （解）

【例1-25】 求两平面的交线，并判断可见性，如图1-25（题）所示。

【解】 本题主要考查两一般位置平面相交求交线。一般位置平面相交求交线可视为两个一般位置直线和一般位置平面求交点的过程，本题中，可视为分别求DE和EF直线与平面ABC的交点，两交点的连线即为两平面的交线。包含DE直线作正垂面Pv，包含EF直线作正垂面Rv，然后求出DE与ABC的交点M点，EF与ABC的交点N点，连接即为交线。可见性的判别采用重影点的判别方法，结果如图1-25（解）所示。

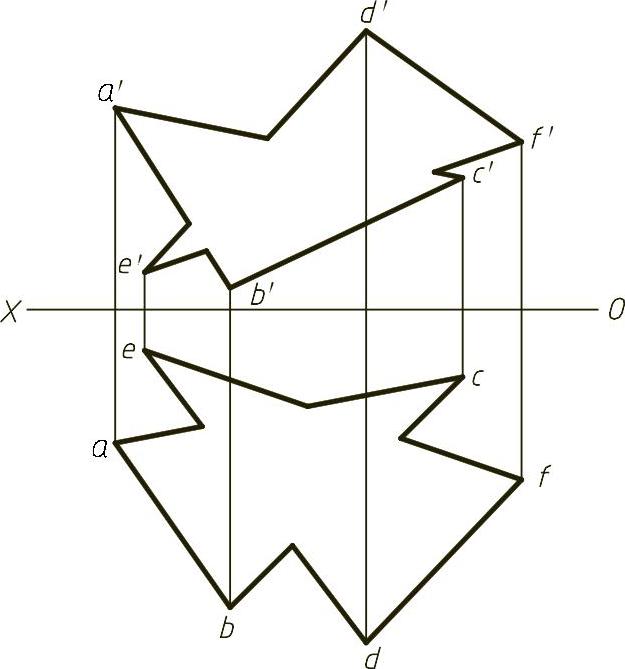
图1-25 （题）

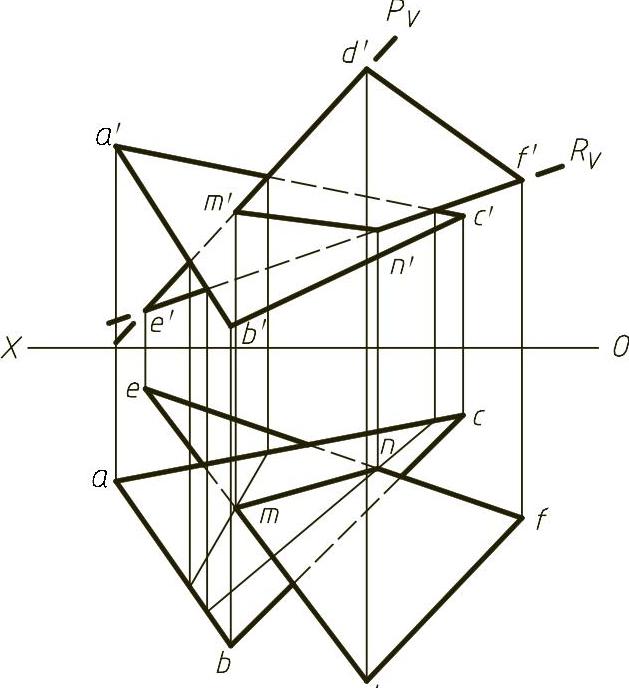
图1-25 （解）

【例1-26】 以水平线BC为边作一正方形BCDE，使之垂直于三角形ABC，如图1-26（题）所示。

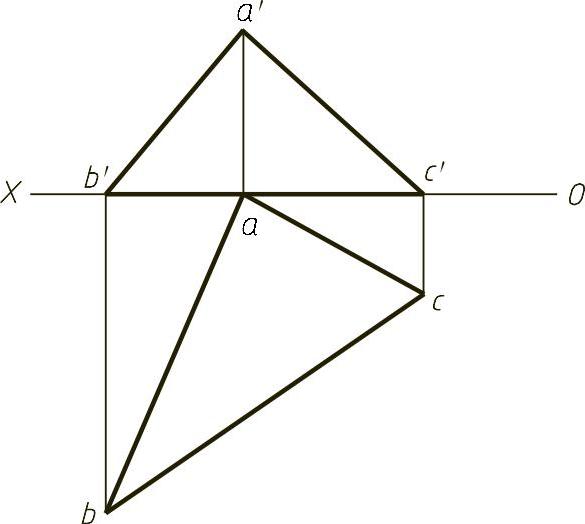
图1-26 （题）

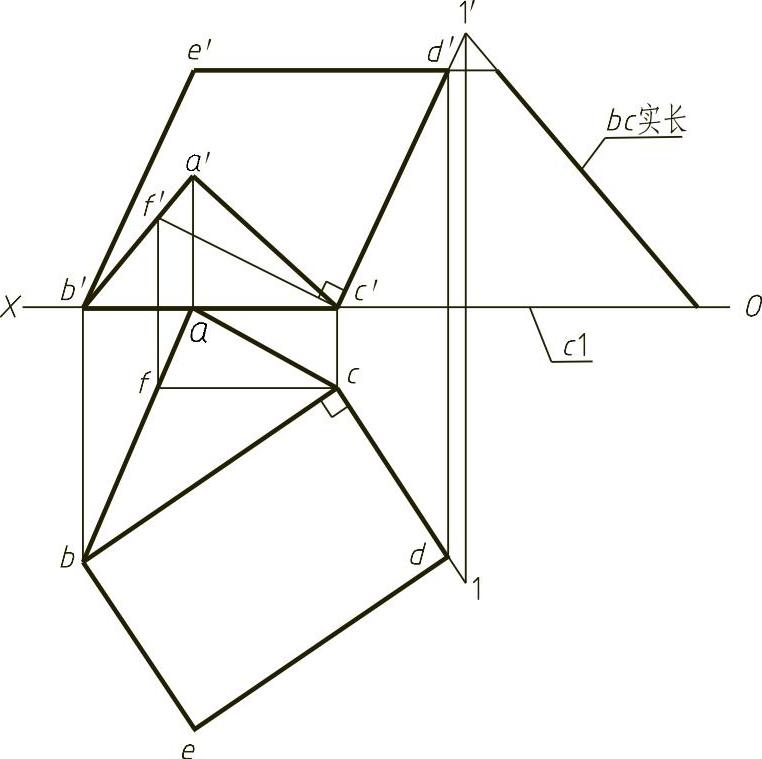
图1-26 （解）

【解】 本题主要考查两平面垂直的几何条件。首先在ABC平面内作一条正平线CF，然后过c作c1垂直于bc，过c′作c′1′垂直于c′f′，这样就作出了一条与ABC平面垂直的直线，要作的平面只要包含该直线，即垂直于平面ABC。接着用直角三角形法求CⅠ直线的实长，在CⅠ直线的实长上截取等于BC实长的一段，可确定D点，最后根据正方形对边平行可确定E点，正方形BCDE的两面投影完成。结果如图1-26（解）所示。

【例1-27】 已知AB、CD为正交两直线，作直线AB的水平投影，如图1-27（题）所示。

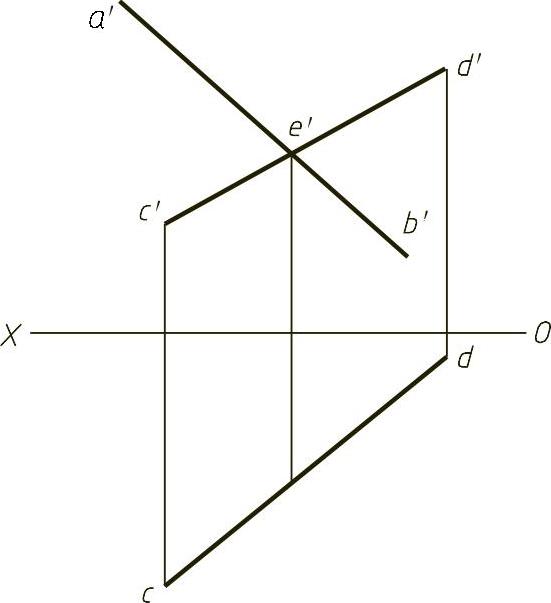
图1-27 （题）

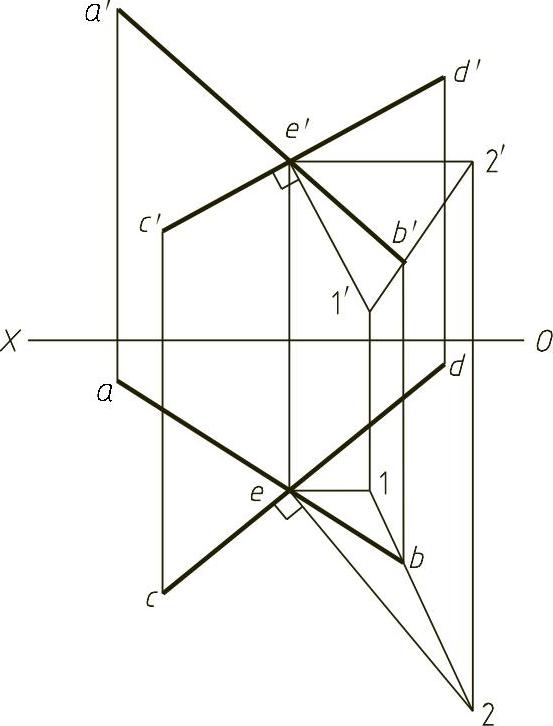
图1-27 （解）

【解】 本题主要考查线面垂直的几何条件以及平面上取线。AB和CD既然相互垂直并且相交，AB必在过E点且垂直于CD的平面上。因此，求解时，首先过E点构造正平线EⅠ和水平线EⅡ，分别保证e2垂直于cd，e′1′垂直于c′d′，这样就建立了过E点且垂直于CD的平面EⅠⅡ，然后根据平面上取点的方法即可确定B点的水平投影，连接be延长后与过a′投影线的交点即为a点，连接ab，完成直线AB的水平投影。结果如图1-27（解）所示。