【例1-14】 已知AB直线与三角形平面CDE相交于B点,且B点距V面等于20mm,补全AB的两面投影,如图1-14(题)所示。
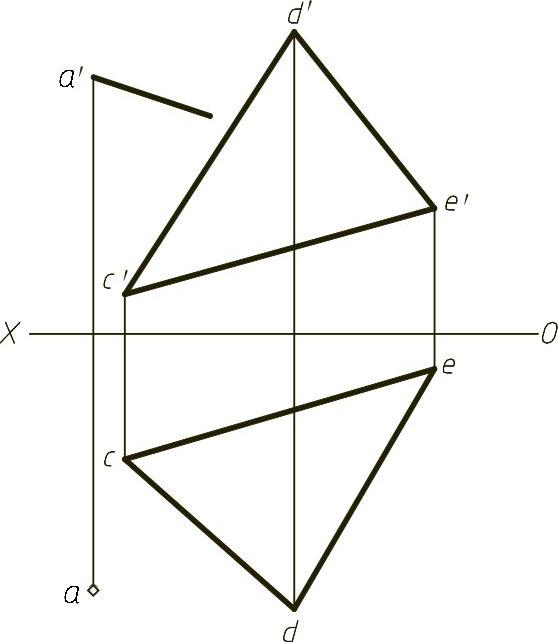
图1-14 (题)
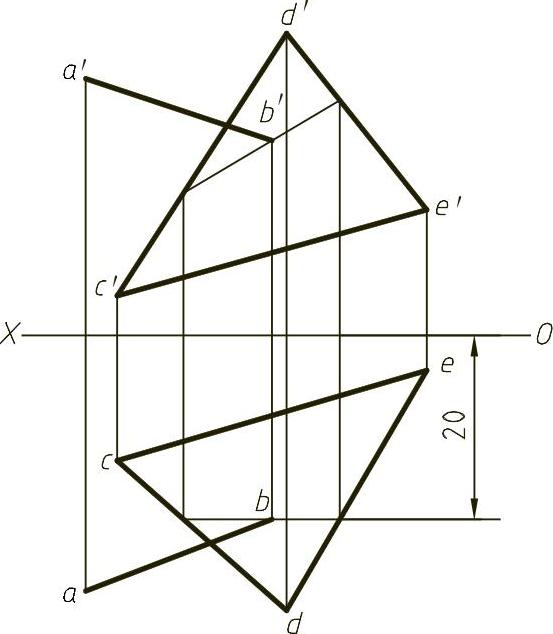
图1-14 (解)
【解】 本题主要考查属于平面上点的投影特性。B点是AB与平面的交点,既在线上又在面上,且B点又距V面20mm,则先作出距V面20mm且属于CDE平面的正平线,再在AB线上确定B点,结果如图1-14(解)。
【例1-15】 已知AD为正平线,完成平面图形ABCD的投影,如图1-15(题)所示。
【解】 本题主要考查平面的表示方法以及平面上取点的方法。由AD为正平线,可以首先求出D点的水平投影,再通过正面投影添加辅助线a′c′与b′d′,利用直线上取点的方法可确定C点的水平投影。作图结果如图1-15(解)所示。
【例1-16】 已知矩形平面ABCD的点D在直线EF上,完成矩形的两面投影,图1-16(题)所示。
【解】 本题主要考查直角投影定理。由AB直线的两面投影知其为正平线,矩形的各条边相互垂直,因此与AD垂直于AB,并且D点在EF直线上,根据直角投影定理,过a′作a′b′的垂线,与e′f′的交点即为d′,根据对应关系作出d点,然后根据对边平行分别过B点和D点的两面投影作平行线可求出C点的两面投影,连接完成矩形的两面投影,结果如图1-16(解)所示。
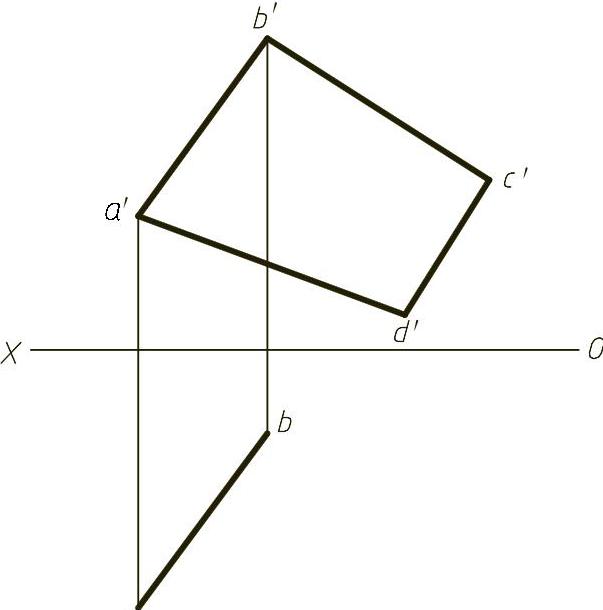
图1-15 (题)
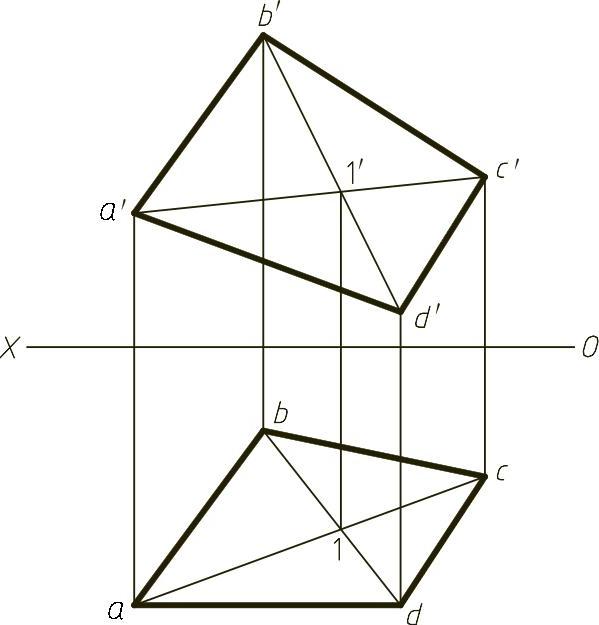
图1-15 (解)
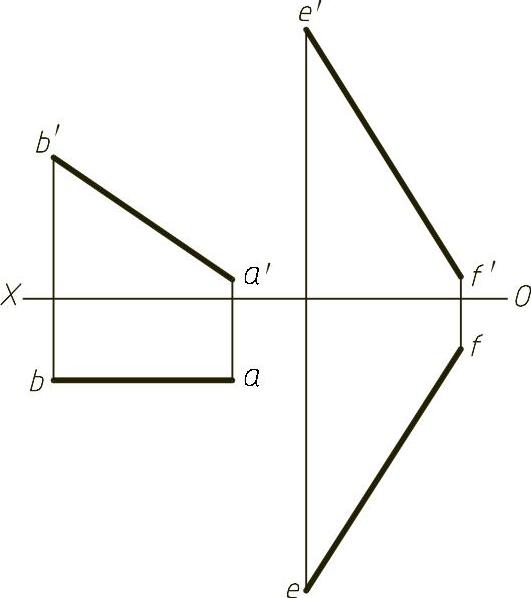
图1-16 (题)(https://www.xing528.com)
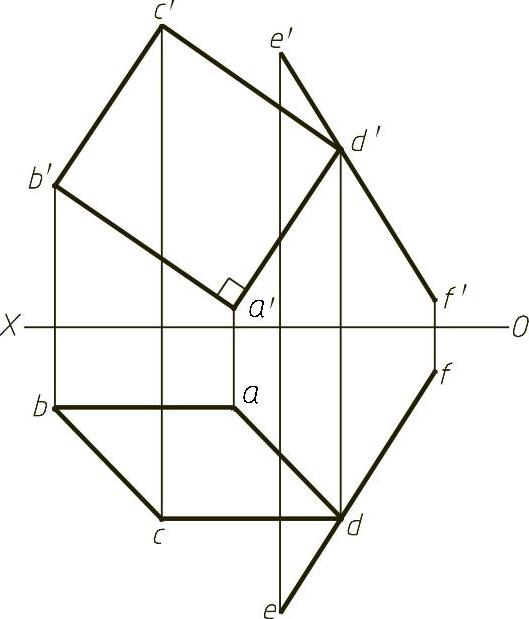
图1-16 (解)
【例1-17】 判别四点A、B、C、D是否属于同一平面,如图1-17(题)所示。
【解】 本题主要考查平面上取点。首先连接A、B、C三点可以构成一个平面,然后判断D点是不是在平面ABC上。如果在,则四点同属于一个平面;如果不在,则四点不属于同一平面。添加辅助线be通过d点,然后作出正面投影b′e′,可以看出d′不在b′e′上,因此判定D点不在ABC平面上,因此四点不属于同一平面,如图1-17(解)所示。
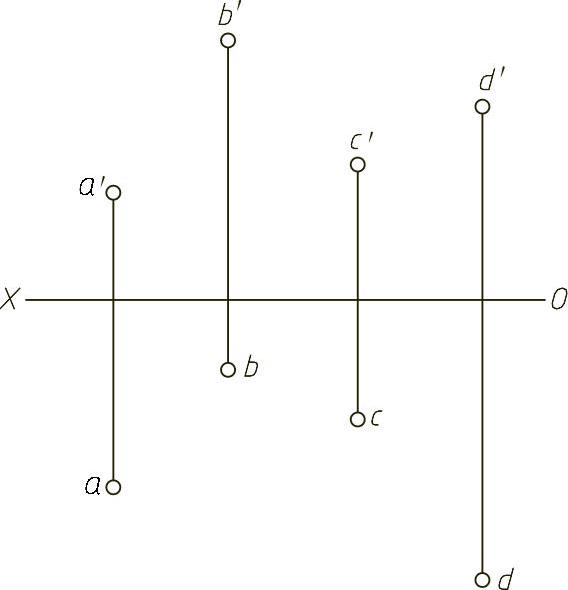
图1-17 (题)
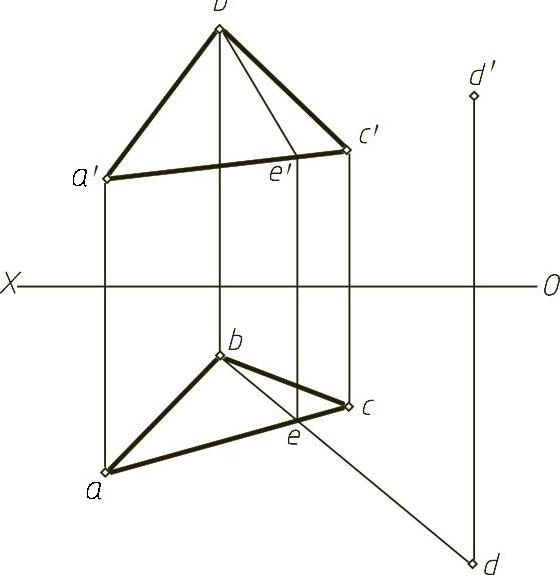
图1-17 (解)
【例1-18】 给定一平面ABC,作属于该平面的水平线,该线在H面上方且距H面等于10mm;作属于该平面的正平线,该线在V面前方,且距V面等于25mm,如图1-18(题)所示。
【解】 本题主要考查平面上取直线。作水平线,在OX轴的上方距OX轴等于10mm作平行于轴线的直线,直线与a′c′交于d′,与b′c′交于e′,连接d′e′即为水平线的正面投影,向下作投影线可以作出de;作正平线,在OX轴的下方距OX轴等于25mm作平行于轴线的直线,直线与ac交于f,与ab交于g,连接fg即为正平线的水平投影,向上作投影线可以作出f′g′。解题结果如图1-18(解)所示。
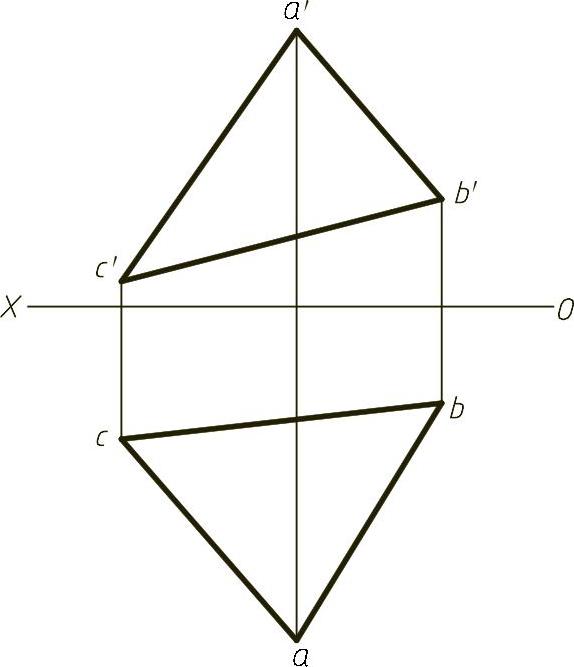
图1-18 (题)
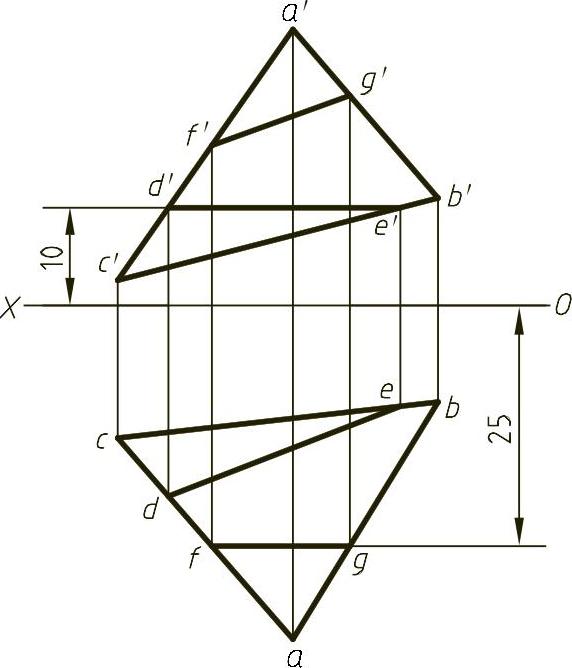
图1-18 (解)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




