平面图形ABCDE的水平投影和H面、V面的距离确定方法

【例1-11】 已知直线AB属于已知平面MNEF，求直线AB的另一投影，如图1-11（题）所示。

图1-11 （题）

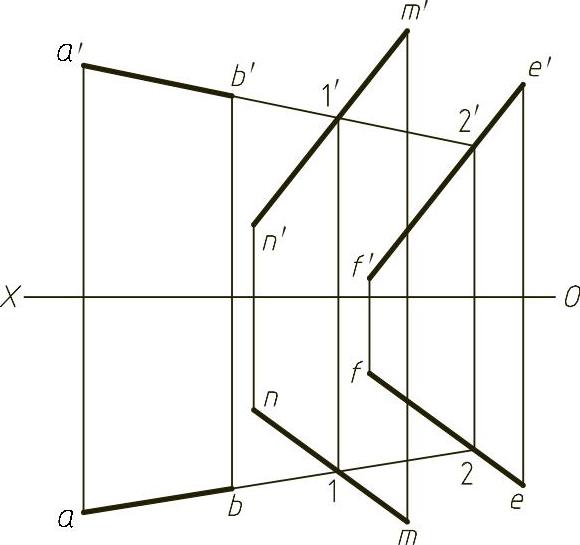
图1-11 （解）

【解】 1.分析

本题主要考查属于平面的直线的投影特性。

2.步骤

1）延长a′b′交m′n′、e′f′分别于1′和2′点。

2）作直线ⅠⅡ的水平投影12，并延长。

3）过a′和b′作投影线，与12延长线的交点即为a和b点，连接，得到AB的水平投影ab，结果如图1-11（解）所示。

【例1-12】 在平面ABC内取一点M，使其距离H面等于18mm，距离V面等于28mm，如图1-12（题）所示。

【解】 1.分析

本题主要考查平面内取点和取直线的方法，题中所求的M点在距H面18mm且在ABC平面内的一条水平线上，同时满足距V面等于28mm，因此只需在此水平线上找一距V面28mm的点即可。

2.步骤

1）在OX轴上方距OX轴18mm作平行于OX轴的直线，交a′b′于1′点，交a′c′于2′点，在ab和ac上确定1、2点，连接12。

2）在OX轴下方距OX轴28mm作平行OX轴的直线，交12与m点，在1′2′上由m点确定m′点，即为所求，结果如图1-12（解）所示。(www.xing528.com)

【例1-13】 已知AB为正平线，补全平面图形ABCDE的水平投影，如图1-13（题）所示。

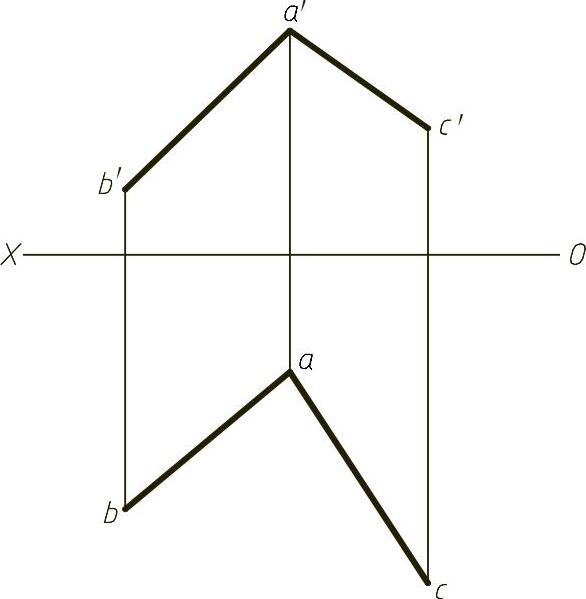
图1-12 （题）

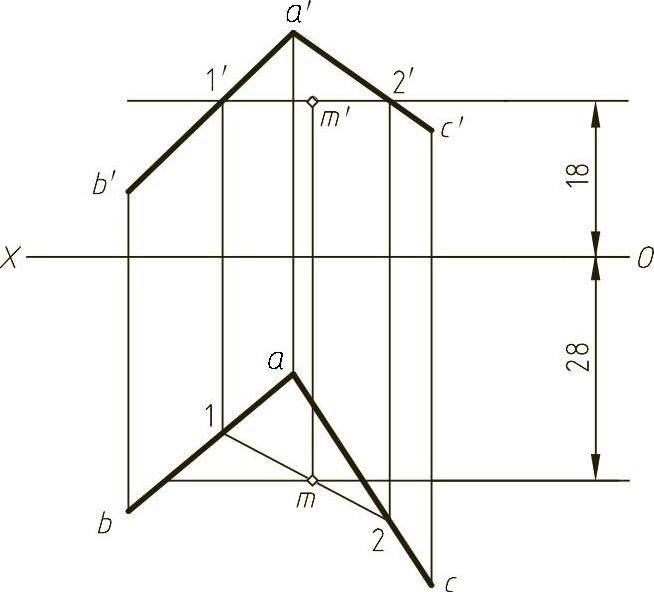
图1-12 （解）

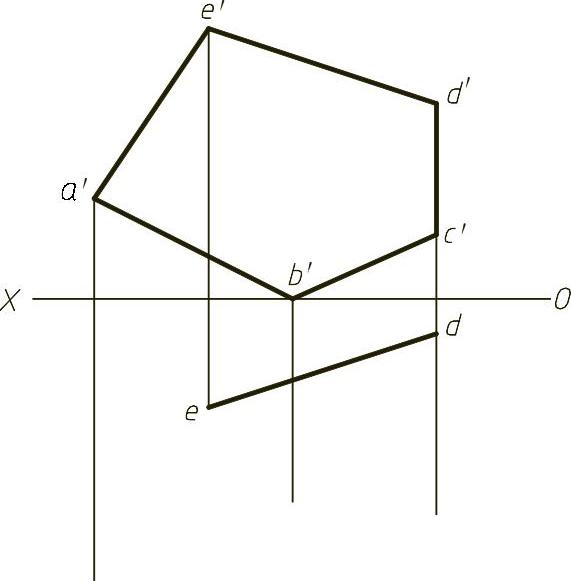
图1-13 （题）

图1-13 （解）

【解】 1.分析

本题主要考查平面的表示方法、平面上取点和取直线的方式直线的投影特性以及点分直线的定比性等。解该题的关键是如何把握AB是正平线这个条件。由于a、b两点不知，AB的水平投影无法直接作出，但在该平面内，过E点或D点（这两点已知）同样可以作出与AB平行的正平线，由此演变为由ED和过E或D点的一条正平线构成ABCDE平面。

2.步骤

1）过e′点作e′2′平行于a′b′，交c′d′于2′点，过e点作e2平行于OX轴，用点分直线成定比的特性作出c点。

2）连接a′d′，交e′2′于1′点，在e2上作出1点，连接d1，延长后与过a′的投影线相交得到a点。

3）过a点作平行于OX轴的直线，与过b′的投影线的交点即为b点。

4）连接abcde，即为所求，结果如图1-13（解）所示。