所谓组合逻辑电路的分析,就是对给定的组合逻辑电路找出其输出与输入之间的逻辑关系,分析出组合逻辑电路的功能。
组合逻辑电路分析步骤如图4-1所示,具体步骤如下:
![]()
图4-1 组合逻辑电路分析步骤
(1)根据逻辑电路图,写出输出变量对应于输入变量的逻辑函数表达式。
具体方法是:由输入端逐级向后递推,写出每个门输出对应于输入的逻辑关系式,最后推出输出信号对应于输入的逻辑表达式。得到的表达式可能不是与或式,也可能太复杂,不利于列真值表,因此需要做相应的化简与变形,为了方便下一步列写真值表,因此,并不需要得到最简与或式,一般来说得到与或式即可。
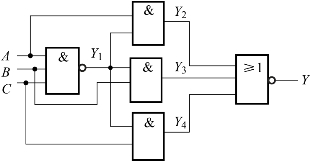
图4-2 例4-1逻辑电路图
(2)根据输出逻辑表达式列出真值表。
将输入信号所有可能的取值组合代入化简后的逻辑表达式中进行计算,列出真值表。
(3)根据逻辑表达式和真值表,对电路进行分析,最后确定电路逻辑功能。
例4-1 分析图4-2所示组合逻辑电路的功能。
(1)根据图4-2所示逻辑电路图,逐级推导得到逻辑表达式。

(2)列出真值表。
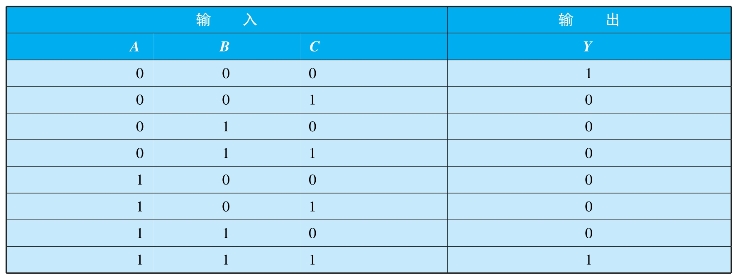
将A、B、C各种输入组合代入Y表达式可得对应的逻辑值,列出如表4-1所示的真值表。
表4-1 例4-1真值表(https://www.xing528.com)
(3)分析确定电路逻辑功能。
通过对真值表观察,可发现当A、B、C三个输入变量取值一致时,输出为1,否则为0。所以该电路是一个用来对输入信号进行判断的电路,称其为“一致判断电路”。
例4-2 试分析图4-3所示电路的逻辑功能。
如图4-3所示,电路有两输出端S、C,故是多输出组合逻辑电路,它由五个与非门构成,其分析过程如下:
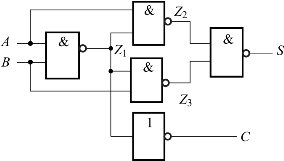
图4-3 例4-2逻辑电路图
(1)根据图4-3所示电路图,由逐级递推法写出输出S、C的逻辑表达式。

(2)列出真值表。
将A、B各种输入组合代入S、C表达式,可得对应的逻辑值,列出真值表,如表4-2所示。
表4-2 例4-2真值表

(3)电路逻辑功能分析。
由表4-2真值表可以看出,如果将A、B看成两个一位的二进制数,则电路可实现两个二进制数相加的功能。S是两个一位二进制数相加的和,C是向高位的进位。由于这一加法器电路没有考虑低位的进位,所以该电路为半加器,可作为运算器的基本单元电路。

组合逻辑电路的分析
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




