空气单元：从概念到应用

排水孔是一个充满空气或水体的中空柱状体，也可以看作是比一般介质的渗透性大得多的特殊介质，可用恰当的渗透系数来表征排水孔的渗透性能，于是前处理工作中只需给出排水孔孔口处结点的水头值。由于将排水孔中的空气看作是一种渗流介质，故将此类单元命名为“空气单元”。

对排水孔单元赋予一定的渗透系数而将其加入到整体网格中计算，省却了给定其内壁各点边界条件的麻烦。但是，应该用什么样的渗透系数来正确反映其特性呢？为方便研究，取排水孔渗透系数k d与其周边介质渗透系数k r的比值R（R=k d/k r）为相对渗透系数，进行敏感性分析，研究其合理取值的问题。在实际工程应用时，根据具体情况，将排水孔周边介质的渗透系数扩大R倍，即得到所研究问题中排水孔的虚拟渗透系数。

图3-5-1　含一个排水孔的岩石块体有限元网格

讨论两种排水孔形式：①孔口出流式，即水从孔内壁逸出后从上部孔口流出，此时孔内壁各结点的水头相同，等于孔口的位置水头；②孔壁逸出式，即水从孔内壁逸出后从下部孔口流出，此时孔内壁为地下水的逸出面，孔壁上各结点的水头与其各自的位置高程相等。

1.孔口出流式

图3-5-1所示为含一个排水孔的各向同性岩石块体，4个侧面及上表面均为定水头边界，水头值分别取为3.5m和3m，底面为不透水边界。岩体的渗透系数为1，排水孔渗透系数为R。

采用两种方法进行渗流计算：①在计算中抛弃排水孔处单元，给定排水孔内壁上各点的水头值，即弃单元法，这是一种较为精确的方法；②采用本章提出的空气单元法。通过计算，可以得到两种方法的计算误差E与相对渗透系数R的关系。

以弃单元法的计算结果为基准，得到计算成果如下：

（1）由图3-5-2可以看出，排水孔内壁的计算误差E随着排水孔渗透系数R的增大而减小。当lg R＜3时，误差E随着R的增大明显减小；当lg R≥3时，误差E可控制在5%以内。由于计算机位数的限制，lg R的最大值取为10。当3≤lg R≤10时，随着R的增大，误差E在0.1%左右振荡。如果认为计算误差在5%内可行，则当以空气单元模拟孔口出流式排水孔时，可取lg R为3，即取排水孔的渗透系数为周边介质渗透系数的1000倍。

图3-5-2　不同排水孔径的E—lg　R关系曲线

图3-5-3　E—D关系曲线

图3-5-4　E—r关系曲线

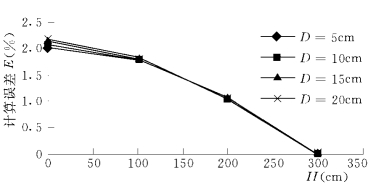
图3-5-5　E—H关系曲线

（2）由图3-5-3可以看出，改变排水孔孔径D，对误差E并无显著影响。说明采用空气单元时，相对渗透系数的取值与孔径大小无明显关系。(www.xing528.com)

（3）选取距排水孔中心不同距离r处的点，绘制E—r曲线，如图3-5-4所示。可以看出，误差基本上随着r的增大而减小，在排水孔孔壁上误差最大。

（4）以排水孔内壁底部为参照，选取不同高度H的点，绘制E—H关系曲线，如图3-5-5所示。可以看出，排水孔内壁底部的误差最大。

2.孔壁逸出式

图3-5-6为各向均匀岩体中隧洞的有限单元法网格，沿洞顶中心线设一垂直排水孔。岩体左侧与右侧均为定水头边界，水头值为15m。隧洞周边壁亦为定水头边界，水头值与各结点的位置高程相等。排水孔半径为0.1m，由洞顶延至岩体上表面。岩体渗透系数为1，排水孔渗透系数为R。

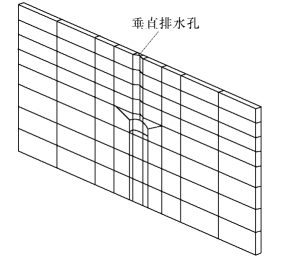
图3-5-6　含一个垂直排水孔的隧洞

在弃单元法的计算中，排水孔内壁各结点应预先给定水头值（与其各自的位置高程相等）。采用空气单元时，无需给定孔内边壁各点的定水头值，只要给定排水孔的渗透系数R即可。

经过对比分析，获得以下结论：

（1）与孔口出流式排水孔的有关结论相同，在孔壁逸出式排水孔中，相对渗透系数R的取值与孔径大小无显著关系，且在排水孔壁上误差最大。

（2）从图3-5-7可以看出，当2.1＜lg R≤2.7时，排水孔内壁的计算误差E可控制在5%以内。当lg R＞2.7或lg R＜2.1时，误差E显著变大。若认为计算误差在5%内可行，则在以空气单元模拟孔壁逸出式排水孔时，可取lg R为2.5，即排水孔的渗透系数为周边介质渗透系数的300倍。

图3-5-7　不同排水孔径的E—lg　R关系曲线

图3-5-8是弃单元法计算的排水孔中心线铅直断面的渗流等势线分布，图3-5-9是空气单元法计算的同一断面的渗流等势线分布。二者对比可以看出，当选取合适的排水孔渗透系数后，空气单元法以较高的精度接近弃单元法。图3-5-10是两种方法计算的自由面。

图3-5-8　弃单元法计算的渗流等势线分布（单位：m）

图3-5-9　空气单元法计算的渗流等势线分布（单位：m）

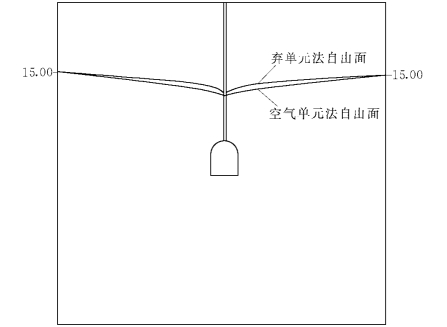
图3-5-10　自由面对比图