【摘要】：子单元不必是标准的常规有限单元。求解出结点位移后，便可计算出每个子单元内的位移、应力和应变。作用于子单元的荷载被转移到复合单元的结点上，根据虚功原理可推出该复合单元的平衡方程。式的插值表达式只对相应的子单元有效。
一、锚杆
考察一个岩石单元r（图3-1-1），其中包含nb个锚杆子域，对应的还有ng个砂浆子域。岩石r与砂浆g的接触面记为j r，g，砂浆g与锚杆b的接触面记为j g，b。该岩石单元便是复合单元，子域称为子单元。子单元不必是标准的常规有限单元。在子单元内的位移
图3-1-1 含锚杆的复合单元
图3-1-2 含锚杆的复合单元内的位移插值
{Δu}r、{Δu}g、{Δu}b可由定义于复合单元结点上的位移插值求出（图3-1-2）
式（3-1-1）中，[N]是定义于整个复合单元内的常规有限单元的形函数。需指出的是，由式（3-1-1）表达的插值公式仅在各自子单元内有效。作用于子单元的荷载被转移到复合单元的结点上，根据虚功原理可推出该复合单元的平衡方程。求解出结点位移后，便可计算出每个子单元内的位移、应力和应变。(www.xing528.com)
二、结构面
图3-1-3所示的是一个被两条结构面分割成4个子域的岩体单元，两条结构面被相互分割成4个结构面段（节理段），这4个子域也成为子单元。同样，子单元不必是标准的有限单元。一般情况下，记nr为子单元的个数，j rlrm为子单元rl和rm之间的结构面，则子单元rl内的位移{Δu}rl由复合单元的结点位移{Δδ}rl插值得到（图3-1-4）。
式（3-1-2）中，[N]是常规有限元法中定义的形函数。式（3-1-2）的插值表达式只对相应的子单元有效。子单元上的荷载应转换为复合单元的相应结点荷载，然后根据虚功原理建立平衡方程。解得结点位移后，每个子单元的位移、应变和应力即可求得。
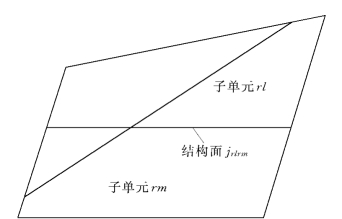
图3-1-3 含结构面的复合单元
图3-1-4 含结构面的复合单元内的位移插值
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
