坝基、坝肩与拱坝运行期耦合分析

一、计算条件

拱坝坝身混凝土的弹性模量取为E=21GPa，泊松比取为μ=0.18。

计算域上游以Y=37000m为边界，下游以Y=36300m为边界，左岸以X=14000m为边界，右岸以X=12900m为边界，底部高程为700.00m。整体坐标原点为（13000，36000，0）。计算域上下游及左右岸边界取法向位移约束，底部取垂直位移约束。

用块体单元识别方法，建立了稳定分析的小湾拱坝坝身拱梁系统和坝肩块体单元系统（图2-8-12和图2-8-13），共有块体单元2231个，拱梁单元88个（9拱17梁）。

其他条件与本章第二节相同。

二、计算荷载

1.自重

岩体的容重取为γr=27k N/m3，混凝土的容重取为γc=24k N/m3。2.渗流

与本章第三节相同。

3.静水压力

拱坝上下游静水压力计算中，取水的容重为γw=9.8k N/m3。上游水位1240.00m，下游水位1004.00m。

4.泥沙压力

淤沙高程为1097.00m，浮容重为γs=9.5k N/m3。

5.温度荷载

取温降情况，由结点的温度变化值计算出拱向的荷载，再转化为相应的结点荷载。表2-8-5和表2-8-6分别是坝面结点的平均温降和线性温降。

6.荷载模拟顺序

首先考虑天然地下水渗流场，施加岩体自重，近似模拟天然地应力场；然后，考虑拱坝完建、施加自重、水库蓄水后，在坝身施加静水压力、泥沙压力、温度荷载，并考虑岩基渗流场的改变，即正常工况。

三、主要计算成果及分析

1.应力、应变和屈服

图2-8-14和图2-8-15是高程1090.00m和高程1245.00m平切面上的变位图。

坝基左岸最大变位为2.7cm，发生于高程1090.00～1010.00m；右岸最大变位为2.0cm，也发生于高程1090.00～1010.00m。左岸变位大于右岸变位。拱坝变位最大值发生于拱冠梁顶部，为15.44cm。

检查在正常蓄水位工况下的各典型结构面的屈服情况，发现其基本规律与原常规弹粘塑性块体单元法分析结果基本相同（参见本章第三节）。

图2-8-16是正常蓄水位工况下拱冠梁的主应力等值线图，图2-8-17～图2-8-20是上下游坝面应力等值线图，图2-8-21和图2-8-22为上下游面主应力矢量图。拱冠梁上游最大主拉应力为3.84MPa，下游最大主压应力为-16.07MPa。拱圈最大主拉应力发生于高程1245.00m的下游，为1.65MPa；最大主压应力发生于高程1170.00m的上游，为-6.75MPa。

表2-8-5　坝面结点的平均温降

表2-8-6　坝面结点的线性温降

图2-8-12　小湾拱坝坝身拱梁系统和坝肩块体单元系统轴测图(www.xing528.com)

（a）右岸；（b）左岸

图2-8-13　小湾拱坝坝身拱梁系统和坝肩块体单元系统渲染效果图

图2-8-14　高程1090.00m位移矢量图

图2-8-17　上游面σx等值线图（单位：MPa）

图2-8-18　上游面σz等值线图（单位：MPa）

图2-8-19　下游面σx等值线图（单位：MPa）

图2-8-20　下游面σz等值线图（单位：MPa）

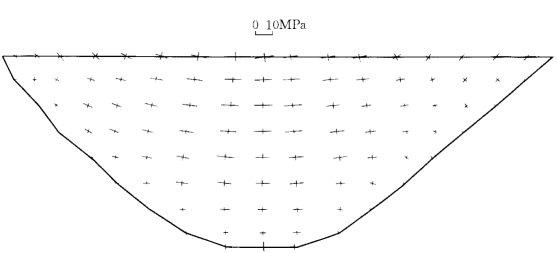
图2-8-21　上游面主应力矢量图

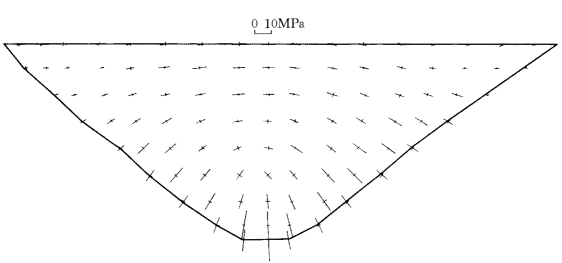
图2-8-22　下游面主应力矢量图

2.安全系数

表2-8-7列出了安全度较小或比较重要的15种滑动块体单元组合及对应的强度储备安全系数，并列出了原拱梁分载法+常规弹粘塑性块体单元法分析结果（可对照表2-8-4）。

3.主要结论

（1）在正常蓄水位工况下，岩体基本上处于弹性状态，屈服范围很小，且伏格特法基础上的拱梁分载法具有一定的精度，故拱梁分载法+常规弹粘塑性块体单元法分别应用于坝身与坝肩分析的结果与弹粘塑性块体单元法和拱梁分载法耦合分析的结果两者相比，差别不大。

（2）在进行降强分析推求安全系数时，由于坝肩岩体变位增大，非线性变形逐渐占主导地位，拱坝应力和拱端推力都发生较大变化，从而弹粘塑性块体单元法与拱梁分载法的耦合分析与拱梁分载法+常规弹粘塑性块体单元法的结果有一定的差异，差异的大小与可能破坏的滑动块体单元组合位置有关。

表2-8-7　滑动块体单元组合及对应的安全系数

1）第1号、2号、3号、4号、10号和11号滑动块体单元组合离坝肩较远，不直接受拱坝推力影响，破坏的主要因素是自重作用，故两种方法的安全系数差异较小。

2）第15号滑动块体单元组合位于坝肩上部，承受的拱坝推力不大，在该部位岩体变位较大时，由于拱坝的整体作用，大部分推力可以传递到其他部位，故耦合分析的安全系数增大。

3）对于坝肩中部的主要受力岩体，如第8号、9号和12号滑动块体单元组合，在变位较大时，推力反而有向该部位集中的趋势，故安全系数有所降低。