P 型自适应分析：优化方法探讨

p型自适应块体单元法的概念与p型自适应有限单元法基本相似。其基本思想是：由常规单元结合数量逐渐增加的附加自由度而构成p型单元，这些附加自由度以不违背位移连续条件的逐次升幂多项式函数作为基函数，按照一般的力学分析方法建立代数方程组求解，然后对解进行误差估计并根据误差情况进行基函数阶次的调整。本篇第四章中研究的阶谱块体单元法已具有p型有限单元法的这种特征，但是尚不具有误差估计和根据误差情况自动调整基函数阶次的能力。

在阶谱块体单元法中，各个块体单元计算精度取决于所指定的基函数的幂次，不同单元的计算精度可能会相差很大。如果对单元采取了相对于所需精度偏低的阶次，则计算精度不能满足要求；如果对单元采取了偏高的阶次，则又会造成计算量不必要的增加。为了获得各个单元之间误差基本均衡的、比较客观的单元阶次，需要采用一定的方法对计算误差进行估计，并根据计算误差情况对阶次进行调整。

自适应分析技术在有限单元法中的研究已经相当多了（Holzer，Yosibash，1996；王周宏，胡于进，1999；Düster，Bröker，Rank，2001），在边界单元法（金朝嵩，2000）、无单元法（Duarte，Oden，1996；刘欣，朱德懋，陆明万，张雄，2000）、数值流形方法（居炎飞，章光，王水林，2001）中的研究也已经开展。笔者对阶谱块体单元法的p型自适应技术进行了研究（Chen，Li，Wang，Shahrour，2004；汪卫明，陈胜宏，2005）。

一、后验误差估计

在有限单元法中，误差估计主要采用基于应力平滑技术、基于残量或基于外推技术的方法，其中，p型有限单元法主要采用基于外推技术的误差估计方法。但是在阶谱块体单元法中，由于使用了覆盖单元，应力平滑技术或应力外推技术很难实现；并且，在有限单元法中，误差估计往往是为了使得单元之间的应力成为连续变化（Zienkiewicz，Zhu，1991），而对于天然块体单元而言，结构面两侧块体单元的应力本来就是不连续的。因此，有限单元法中误差估计的有关理论在此不能直接引用，需要加以改造。

定义块体单元rl误差的能量范数为

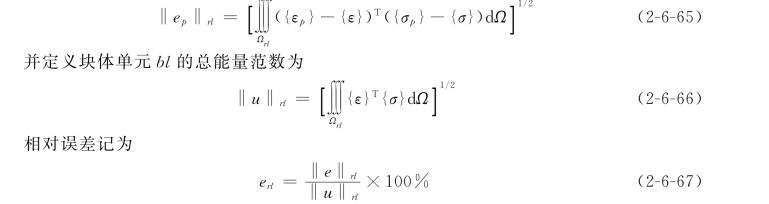
当相对误差小于或等于块体单元的允许误差时，即当满足

时，认为形函数的阶次是合适的，不需要再调整；否则，将形函数阶次升高一阶后进入下一个升阶步的计算。

与有限单元法的情况相同，精确解{ε}和{σ}实际上不可得。笔者直接采用高一阶结果作为升阶调整时的精确解的“最佳猜测”。这时，能量范数的等价形式为

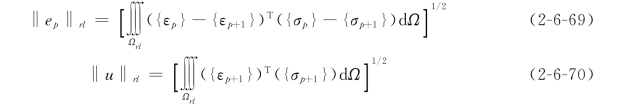
当某个单元的误差满足要求时，该块体单元的形函数阶次就固定在p+1。当所有块体单元的误差都满足后，p型自适应迭代结束。

二、算例考核

图2-6-5是一个简化的重力坝断面。X轴顺河向，Y轴与坝轴线平行，Z轴朝上。地基中含5条断层，将坝与地基的接触面也作为一条结构面B，它们把结构离散为14个块体单元。计算参数列于表2-6-7和表2-6-8。

表2-6-7　岩石与混凝土的计算参数

表2-6-8　结构面的计算参数

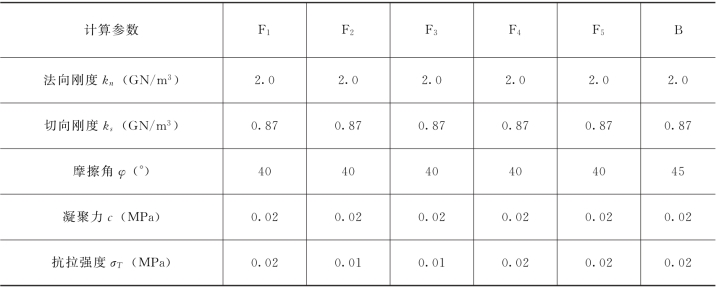
图2-6-5　重力坝算例(www.xing528.com)

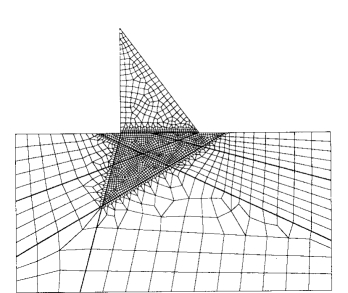
图2-6-6　有限单元网格（4358个结点，2109个单元）

地基的初始应力由下式计算

库水的作用按施加于坝面和库底的面力考虑。

取10m厚坝段，采用自适应块体单元法和有限单元法对该算例进行研究。图2-6-6是X-Z面内的有限单元网格。

在块体单元法分析中，Y方向的形函数固定于1阶，X-Z面内的形函数进行自适应调整。

总自由度、能量范数、相对误差以及坝顶位移列于表2-6-9，各块体单元最终的形函数阶数及自由度列于表2-6-10。自适应块体单元法和有限单元法的位移计算结果见图2-6-7和图2-6-8，应力计算结果见图2-6-9和图2-6-10。

表2-6-9　自适应计算过程指标

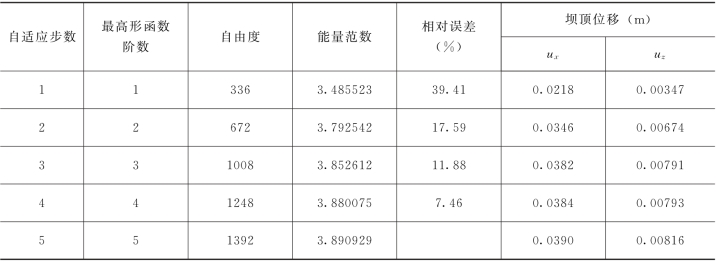
表2-6-10　块体单元的最终阶数与自由度

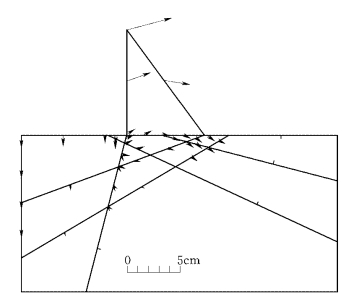
图2-6-7　块体单元法计算的位移矢量

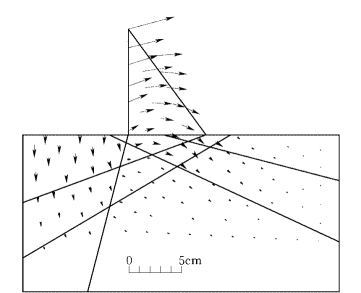
图2-6-8　有限单元法计算的位移矢量

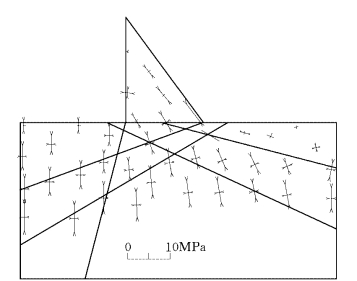
图2-6-9　块体单元法计算的主应力矢量

图2-6-10　有限单元法计算的主应力矢量