如何进行结构开裂分析？

在结构开裂分析方面，目前主要的数值方法仍然是有限单元法（强天驰，寇晓东，周维垣，2000；汪卫明，徐明毅，陈胜宏，2001；陈胜宏，汪卫明，徐明毅，邹丽春，2003）。有限单元法适应性好，但有限单元法的收敛性定理指出，只有增加单元数，能使近似位移场及其一阶导数场处处任意地接近真实场时才能保证算法收敛。对于断裂问题，裂纹尖端附近位移场精确解的一阶导数在裂纹尖端无界，普通常规单元位移模式不能反应裂纹尖端处的奇异性，不满足收敛性条件，即使采用很细的网格也难以达到足够的精度（Chan，Tuba，Wilson，1970；周爱细、黄建龙、郎福元，1998）。而且，在应用于岩体这类不连续介质时，有限单元法还存在对不连续面的有效模拟和网格动态调整困难的问题。

数值流形方法（王水林，葛修润，1997）、无单元法（寇晓东，周维垣，2000）、不连续变形分析方法（吴洪词，1996）也可以模拟岩石块体单元内的裂纹扩展问题，但目前的运用一般局限于二维情形。

块体单元法是一种新兴的数值分析方法，能较好地考虑结构的不连续特性，概念简单，能够处理三维问题，且不需进行接触关系的判断。因此，可以考虑采用阶谱块体单元法来分析岩体的开裂破坏问题（李永明，陈胜宏，王均星，2004）。

在阶谱块体单元法中，如果要模拟天然存在的节理或裂隙的张开或闭合，则单元构形不变，将各结构面的法向应力代入破坏条件，满足开裂条件时，结构面开裂，应力为零。由于结构面内应力调整，结构面应力失去平衡，需将不平衡应力转换成结构面上的附加荷载，在整个块体单元系统内重新进行分配，以达到新的平衡。也可将这些失衡力与下一级荷载增量加在一起计算。

模拟裂缝穿越块体单元破坏的现象比较困难。岩石基本上可视为准脆性材料，可以考虑采用线弹性断裂力学理论来进行分析（于骁中，谯常忻，周群力，1991），然而断裂力学应用于岩石的研究并不像陶瓷、玻璃或金属那样成熟（王元汉等，2000）。用断裂力学的概念和断裂模式研究岩石的断裂过程时，认为断裂的起始和扩展都是原有裂隙和缺陷的发展。但岩体一般位于地下，很难调查清楚初始裂纹的具体情况，因此必须引入一些假定。断裂力学主要研究裂纹尖端的应力奇异性，而这种奇异性只在线弹性断裂且裂纹为完全尖锐的情形下存在，这时线弹性材料裂纹尖端应力为无穷大。对于岩石或混凝土这类准脆性材料而言，裂纹尖端附近实际上存在很多微裂纹，应力集中比线弹性理论所预言的要弱。按照非局部理论，裂纹尖端的应力奇异性不再存在，最大应力是有限的。对于理想塑性材料，裂纹尖端应力为常量（屈服极限值）。

由于岩石断裂力学研究的局限性，尽管从细观和微观的角度对岩石内部的裂隙进行模拟分析是必要的，但在目前，这样的研究离实际工程的需要还有一定的距离。因此，采用阶谱块体单元法模拟裂缝穿越块体单元破坏的现象，尚需进一步研究，笔者在此介绍的也仅仅是一些初步成果。

一、基本原理

1.裂缝模型

目前被广泛采用的有两类裂缝模型：分离裂缝（Discrete Crack）模型和模糊裂缝（Smeared Crack）模型。分离裂缝模型比较直观，能够描述裂缝几何和力学方面的细节，但在裂缝扩展时，结构拓扑关系随之变化，网格信息变化后需进行结构重计算，直至裂缝停止扩展，因此计算量较大。分离裂缝模型比较适用于宏观裂缝已知的情况。模糊裂缝模型认为裂缝在各个方向均可能产生，在采用具有单元的数值方法时，若单元内某些点的应力达到开裂应力，则整个单元都开裂，单元开裂后将被视为正交各向异性材料，即材料在垂直于主拉应力的方向弹性模量降为零（或计入拉伸强化效应），剪切模量通过引入折减系数进行折减。模糊裂缝模型在计算中不必改变结构的拓扑关系，但只能得到开裂范围而不能提供裂缝的具体细节，比较适用于宏观裂缝未知的情况。

本节研究采用的是模糊裂缝模型。

2.二次覆盖

岩石块体单元几何尺度往往较大，在块体单元法中使用模糊裂缝模型时，如果假设块体单元内某些点的应力达到开裂应力就认为整个块体单元都开裂，则可能会失之于粗糙。一种解决办法是，将尺度较大的块体单元通过添加虚拟结构面进行单元细分，如本篇第四章第四节所述，但这样会增加单元数和自由度数。笔者提出了二次覆盖的概念，即将块体单元用一组积分子域（Cells）来进行覆盖。为了与阶谱块体单元法中的覆盖单元相区别，将原来的覆盖单元称为一次覆盖。

图2-6-3　块体单元的一次覆盖和二次覆盖

二次覆盖是为了进行应力释放和修改材料本构关系而引入的。它是在原来覆盖单元的基础上进行的再次剖分（图2-6-3），是与一次覆盖形状相同或相似的“小单元”。一次覆盖是位移场的覆盖，而二次覆盖是应力场和材料场的覆盖。二次覆盖的引入不增加系统的自由度，且只有那些位于块体单元内的积分子域才被纳入计算。每次的开裂应力释放计算在二次覆盖的积分子域内进行。应力释放后，修改单元刚度矩阵并重新形成总刚，求解方程组后进入下一轮迭代。

3.开裂模拟

对于块体单元内的拉伸型或拉剪复合型裂缝，已有很多准则可供选用，其中最大主拉应力准则最为简单。这一准则虽然忽略了很多因素，但抓住了事物的主要矛盾，在大多数情况下，能够足够正确地描述结构受拉伸应力作用而破坏的现象。该准则为(www.xing528.com)

式中：σT为岩体材料的抗拉强度。

在某一级荷载增量下，对于未开裂的积分子域，按常规的弹粘塑性阶谱块体单元法进行计算。如果岩石块体单元内某点受拉开裂，则在此级及以后各级荷载增量作用下，代表该点的积分子域都不能直接承担荷载，超过材料承载能力的荷载（即释放力）要转移到其他部位上去。

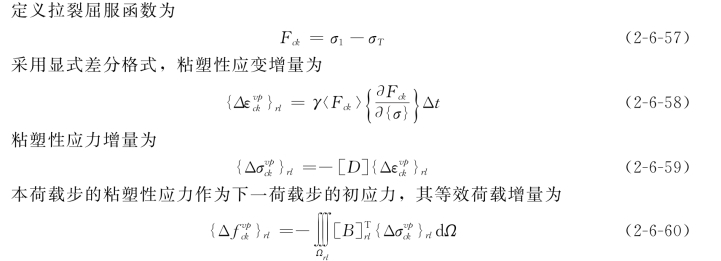
式（2-6-60）中的积分在每一个拉裂的积分子域内进行，[B]rl是进行积分的子域所在块体单元rl的应变矩阵。

开裂以后，子域内的材料成为正交各向异性。设开裂前岩石块体单元的弹性矩阵为

式中：η为残留抗剪系数，反映开裂面的粗糙度及其传递或转移部分剪力的作用，一般取η=0.1～0.5；[R]为坐标转换矩阵。

4.开裂迭代过程

开裂迭代实现过程如下：

（1）弹性计算，得到二次覆盖子域高斯点的弹性应力。

（2）计算二次覆盖子域高斯点的主应力σ1、σ2、σ3。

（3）利用式（2-6-56）判断二次覆盖子域高斯点处是否开裂。若该点未开裂，则按原来的弹粘塑性迭代格式进行迭代计算；若该点开裂，则在式（2-6-57）中取σT=0，然后按式（2-6-60）计算粘塑性应力等效荷载增量，并按粘塑性迭代格式进行应力释放。

二、算例考核

如图2-6-4（a）所示的固端梁，在跨中作用一集中力。将梁的两端作为面约束处理。单元划分情况如图2-6-4（a）所示。逐渐增加集中力，直到梁完全破坏，计算结果如图2-6-4（b）、（c）、（d）所示。图中，梁内部的小方格表示已开裂的子域。

图2-6-4　梁及其拉裂范围