动力分析的现代数值方法及算法研究

在动力分析的现代数值方法中，有限单元法最为成熟。近年来，基于不连续介质模型的动力分析研究也已取得进展（鲁军，张楚汉，王光纶，金峰，1996；金峰，贾伟伟，王光纶，2001）。笔者基于块体单元法建立了一种动力分析算法（Li，Chen，2003），下面予以介绍。

一、基本公式

用块体单元法求解动力问题的过程与有限单元法类似。通过广义质量矩阵、广义刚度矩阵和广义阻尼矩阵将分布于块体单元内部的广义弹性力、广义惯性力和广义阻尼力分别转移到覆盖单元的结点上，基于虚功原理可以推导出块体单元系统的动力方程。

1.阶谱块体单元的广义刚度矩阵

阶谱块体单元的广义刚度矩阵已经在式（2-4-47）的静力方程中定义。

2.阶谱块体单元的广义质量矩阵

将阶谱块体单元rl的质量密度记为ρrl，把块体单元内任意一点的惯性力转移为覆盖单元结点的等效惯性力，则可得到广义协调质量矩阵为

在协调质量矩阵中，建立刚度矩阵和质量矩阵所用的形函数是一致的，位移分配比较合理，因此又称为一致质量矩阵。

为了方便起见，也可以简单地将块体单元的质量平均分配到覆盖单元的结点上形成质量矩阵，并称之为集中质量矩阵。此时，质量矩阵成为对角阵，即

3.阶谱块体单元的广义阻尼矩阵

块体单元rl的Rayleigh阻尼矩阵可以表达为

式中：α和β为系数，根据实测资料确定（朱伯芳，1998）。

4.控制方程

弹性块体单元系统的动力响应由下面的运动方程组控制(www.xing528.com)

式中：{F（t）}为与时间有关的荷载向量；[M]、[C]和[K]分别为与广义位移向量{U}的阶次相匹配的广义质量矩阵、广义阻尼矩阵和广义刚度矩阵。求解运动方程组后，可得到每个块体覆盖单元结点的广义位移响应，继而可计算出广义速度和广义加速度响应。

5.动力方程组的求解

选用Wilson-θ法求解时，动力平衡方程组可以改写为

解出t+θΔt时刻的位移后，t+Δt时刻的加速度、速度和位移即可以算出。具体求解步骤与公式见第一篇第一章第三节，但式（1-1-26）～式（1-1-28）中的结点位移{δ}等量值需换成块体覆盖单元结点的广义位移{U}等量值。

二、算例考核

考察左端固定、右端自由的弹性杆件（图2-6-1）。杆的右端作用有一个集中拉伸力P 0，在t=0时将其释放。研究杆与第一阶振型相应的纵向弹性无阻尼振动。

图2-6-1　左端固定右端自由的杆件及其块体单元划分

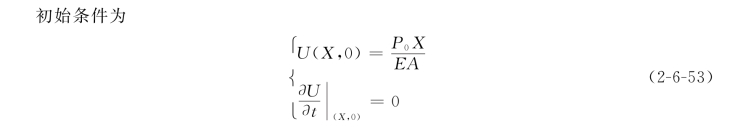
解析解为（王文亮，1993）

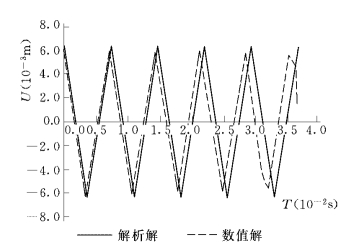
图2-6-2　位移响应数值解和解析解的比较

式中：U 0为杆右端的初始位移，U 0=U（L，0）。

图2-6-2是位移响应的数值解和解析解之间的比较。偏差主要源于数值解中的杆件并非是理想的一维杆件。