不连续岩体的弹粘塑性随机分析方法

近年来，随机分析已被广泛引入结构计算中，随机有限单元法也获得了重视（Cambou，1975；Ghanem，Spanos，1991），但在不连续岩体中，当结构面很多时，随机有限单元法不易实现。

笔者应用一次二阶矩法和蒙特—卡罗法，在块体单元法的基础上构造了不连续岩体的弹粘塑性随机分析方法（Chen，Shen，Huang，1994）。

一、一次二阶矩法

在结构可靠度理论中，极限状态函数g被定义为结构抗力R和荷载效应S的差，当g等于零时，结构达到极限状态。

g是随机变量{p}的函数，即

一次二阶矩法把所有的随机变量转换为标准正态分布N（0，1）变量（期望为零，方差为1），记为（q 1，q 2，…，q N），极限状态方程可表示为N维标准变量空间的超曲面，安全指标β被定义为从原点到超曲面的最短距离，即

1.随机变量的选择

随机变量可组成随机向量的形式，即

式中：N为随机变量的总数。

{p}的期望与方差为

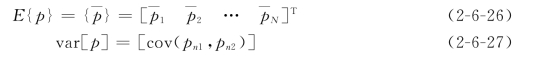
笔者对每个结构面jrlrm考虑了6个随机变量，即

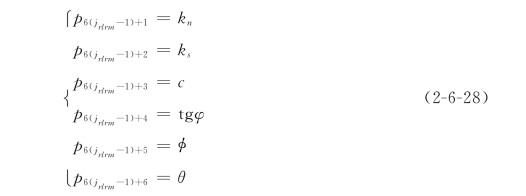
对每个迭代步，必须首先将随机变量在验算点进行正态化。将正态化了的随机向量仍记为{p}，并把矩阵var[p]进行三角分解，即

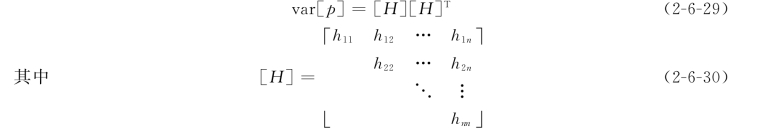
式中：h nn为正态变量p n的均方差。

这样，先前的正态随机向量{p}成为标准随机向量{q}的函数，即

若进一步假设所有的随机变量独立，则有

这种情况下问题大为简化。

2.极限状态函数的选择

不同的破坏机制有不同的极限状态函数。若关注块体单元系统的滑动破坏，则极限状态函数可定义为滑动面上的抗剪强度与剪切力之差。

定义一个破坏模式为沿一个或多个结构面滑动的一个块体单元或块体单元组合。若块体单元系统很大，则有可能存在许多破坏模式，每个破坏模式都有对应的极限状态函数。为节省计算工作量，可先进行常规块体单元法分析，求得若干主要破坏模式。

设第m个破坏模式由l m个结构面切割而成。在第jrlrm面上抗剪强度R jrlrm与剪切力S jrlrm分别为

式中：αjrlrm为第j rlrm面上总剪切力方向与滑动方向的夹角，可由常规块体单元法分析得出。

第m个破坏模式的极限状态函数定义为

其中

3.随机分析算法(www.xing528.com)

由于σz、τzx、τzy是随机向量{p}的函数，故极限状态函数g m是随机向量{p}的隐函数。考虑到式（2-6-31），g m也可表示为标准随机向量{q}的函数，即

式（2-6-41）中，应力的偏导由应力增量的偏导累积而成。根据式（2-2-31），应力增量的偏导为

式（2-6-41）、式（2-6-42）中，对随机变量的偏导数计算比较复杂，细节可参见有关文献（Chen，Shen，Huang，1994）。

二、蒙特—卡罗法

蒙特—卡罗法实现的关键是随机向量的模拟。随机向量的模拟有多种复杂的方法，但若假定所有的随机变量都服从正态分布，则问题大为简化，此时可以方便地用计算机生成伪随机数进行随机模拟。首先需获得在区间（0，1）内均匀分布的随机数列{r}，然后对该数列进行均匀性和独立性审查。由下式计算的随机数列{q 2n}服从N（0，1）分布

按式（2-6-29）把协方差矩阵var[p]分解为三角阵之积，随机向量{p}样本即由式（2-6-31）计算。对每个随机向量{p}样本，首先计算结构面的应力应变状态，然后按式（2-6-35）计算极限状态函数g m，以判断第m个破坏模式是否失稳。若总共进行了N t次模拟，记录到块体单元系统破坏了N f次，则破坏概率为

为保证计算精度，模拟次数必须满足

根据破坏概率P f，易得到安全指标β。

三、算例考核

1.岩坡中的楔形体

对图2-2-1所示岩坡中的楔形体进行考核，计算参数的均值与变异系数列于表2-6-1和表2-6-2，计算结果列于表2-6-3。

表2-6-1　计算参数的均值

表2-6-2　计算参数的变异系数

表2-6-3　楔形体的破坏概率与安全指标

2.复杂边坡问题

对图2-2-13所示边坡实例进行研究，计算参数的均值与变异系数列于表2-6-4和表2-6-5，计算结果列于表2-6-6。

表2-6-4　计算参数的均值

表2-6-5　计算参数的变异系数

表2-6-6　边坡的破坏概率与安全指标

综上所述，利用弹粘塑性块体单元法，可基于一次二阶矩法和蒙特—卡罗法建立不连续岩体的随机分析，其特点是：

（1）相对而言，蒙特—卡罗法较精确，而一次二阶矩法近似性较大。

（2）蒙特—卡罗法不仅可计算各破坏模式的安全指标，同时也可计算块体单元系统的安全指标。一次二阶矩法可计算各破坏模式的安全指标，但只能给出块体单元系统安全指标的上下限。

（3）蒙特—卡罗法需进行大量的随机模拟，每次模拟均需进行一次常规块体单元法计算，若破坏概率很小，则模拟量极大，要求的计算时间很长。相反，一次二阶矩法对验算点的迭代计算量较小。

（4）在目前的计算机条件下，可把蒙特—卡罗法作为一种标准，对一次二阶矩法进行检验。复杂工程实际问题仍以采用一次二阶矩法为宜。