块体单元法与有限单元法的耦合：优化探讨

阶谱块体单元法具有前处理简单的显著优点，特别适合于岩体的变形与稳定分析；而有限单元法理论成熟、体系完善、应用广泛，特别适合于大坝等混凝土结构的应力应变分析。由于这两种数值分析方法各有长短，且可以优势互补，因此建立它们的耦合分析方法是有意义的。

本节介绍笔者提出的一种块体单元和有限单元的耦合分析方法（汪卫明，徐明毅，陈胜宏，2001）。

一、基本理论

考虑到块体单元的几何形状主要由地形和地质条件决定，其顶点与有限单元的结点通常不吻合，故将两种不同类型单元之间的交界面作为一个结构面，通过该结构面的变形协调来实现单元之间的耦合。

在本节中，笔者用rl和fm标识与块体单元和有限单元有关的力学量；用jrlrm标识与块体单元rl和rm之间的结构面有关的力学量；用j rlfm标识与块体单元rl和有限单元fm之间的结构面有关的力学量。

1.块体单元和有限单元耦合模型

在块体单元上采用阶谱位移函数，其构造方法见本篇第四章。

块体单元的位移增量在覆盖单元中的插值可以表示为

式中：[N]rl和{ΔU}rl分别为块体单元rl的位移形函数矩阵和覆盖单元的广义位移增量向量。

有限单元内任意点的位移增量可以通过单元各（广义）结点的（广义）位移增量插值得到，表达式为

式中：[N]fm和{ΔU}fm分别为有限单元fm的位移形函数矩阵和单元结点位移增量向量。有限单元的类型可以是四面体或六面体，其位移形函数矩阵也可以是低阶的、高阶的或阶谱形式的。

如果块体单元rl和rm通过结构面j rlrm相关，则根据几何关系可以得出该结构面上的相对变形增量形式[式（2-4-40）]。

如果块体单元rl和有限单元fm通过结构面j rlfm相关，则该结构面的相对变形增量也可以表示为

块体单元rl的应变增量为

式中：[B]rl为块体单元rl的应变矩阵，具体形式见式（2-4-39）。

有限单元fm的应变增量为

式中：[B]fm为有限单元fm的应变矩阵。

2.本构方程

根据一般的弹粘塑性势理论，采用显格式时步离散，则块体单元或有限单元的应力增量与应变增量的关系都可以表示为

式中：[D]为弹性矩阵；{Δσvp}为粘塑性应力增量向量。因为块体单元和有限单元的本构关系在形式上是一致的，式（2-5-56）对两种单元都适用，故式中省略了下标。

按照关联流动法则，粘塑性应力增量可以表示为

式中：γ为流动参数；Δt为时间步长；F为屈服函数。

若统一记结构面jrlrm和不同单元类型之间的耦合面j rlfm为j，则其应力增量与相对变形增量的关系为

式中：[D]j和{Δσvp}j分别为结构面（或耦合面）j的弹性矩阵和粘塑性应力增量向量。按照关联流动法则，{Δσvp}j的形式为(https://www.xing528.com)

式中：γ为结构面（或耦合面）j的流动参数；F j为结构面j的屈服函数。

3.平衡方程

块体单元和有限单元耦合系统的虚功方程可以表示为

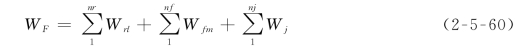
式中：W F为外荷的虚功；W rl为块体单元rl的虚功；W fm为有限单元fm的虚功；W j为结构面j的虚功；nr为块体单元总数；nf为有限单元总数；nj为结构面（包括耦合面）总数。外荷、块体单元rl、有限单元fm和结构面j的虚功分别为

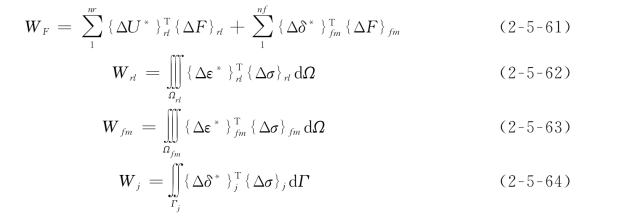
式（2-5-61）～式（2-5-64）中，带上标*的向量表示虚向量。

将式（2-5-61）～式（2-5-64）代入式（2-5-60），整理后可得

式中：[K]、{ΔU}和{ΔF}分别为耦合系统的整体广义刚度矩阵、整体广义位移增量向量和整体广义荷载增量向量。

整体广义刚度矩阵[K]由4种不同类型的子刚度矩阵叠加而成，分别为：块体单元rl的单元广义刚度矩阵[K]rlrl、相关块体单元rl和rm之间的耦合广义刚度矩阵[K]rlrm、有限单元fm的单元（广义）刚度矩阵[K]fmfm，以及相关块体单元rl和有限单元fm之间的耦合广义刚度矩阵[K]rlfm。它们的具体表达形式分别为

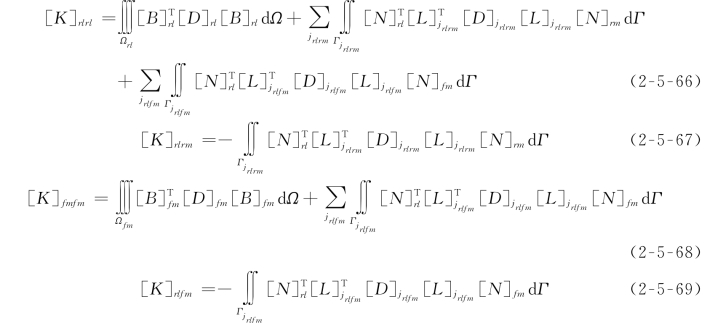
式（2-5-66）中的下标j rlrm对所有与块体单元rl相关的块体单元rm进行循环，下标j rlfm对所有与块体单元rl相关的有限单元fm进行循环；式（2-5-68）中的下标j rlfm对所有与有限单元fm相关的块体单元rl进行循环；式（2-5-67）中的积分在相关块体单元rl和rm之间的结构面j rlrm上进行；式（2-5-69）中的积分在相关块体单元rl和有限单元fm之间的耦合面上进行。

整体广义位移增量向量和整体广义荷载增量向量的具体形式为

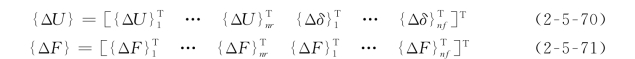
式（2-5-71）中，块体单元rl的广义荷载增量向量{ΔF}rl或有限单元的荷载增量向量{ΔF}fm都由两部分组成，即

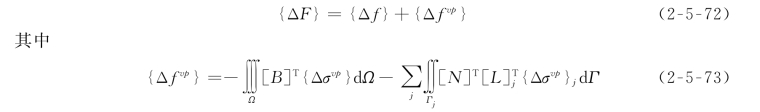
式（2-5-73）对块体单元和有限单元都适用，故省略了下标。{Δf}的形式可由式（2-4-33）～式（2-4-35）表示。

二、算例考核

笔者编制了三维弹粘塑性阶谱块体单元和六面体八结点等参有限单元的耦合分析程序，并以受集中荷载作用的悬臂梁算例进行了考核。

图2-5-12所示是一个自由端受集中荷载作用的悬臂梁，梁长L=6.0m，宽b=0.5m，高h=1.0m，弹性模量为E=10000MPa，截面惯性矩为I，集中力为P=0.5MN。运用有限单元法进行分析时，沿X方向均匀划分为12份，沿Z方向均匀划分为4份，将该悬臂梁划分为48个六面体有限单元。运用阶谱块体单元与有限单元的耦合分析方法对其进行分析时，悬臂梁的左半部分作为一个块体单元，单元形函数沿Y方向（厚度方向）固定取1阶；右半部分均匀划分为24个六面体有限单元（图2-5-13）；两种不同类型单元之间的耦合面的法向刚度系数取为弹性模量的2000倍，切向刚度系数取为弹性模量的1000倍。

图2-5-12　自由端受集中荷载作用的悬臂梁

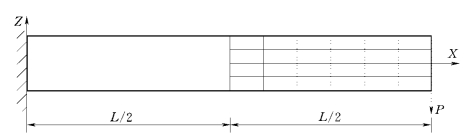
图2-5-13　悬臂梁的块体单元与有限单元耦合模型X—Z剖面图

图2-5-14是悬臂梁的挠度曲线。当块体单元形函数沿X向和Z向取2阶时，计算值与解析值已经很接近；当块体单元形函数沿X向和Z向取3阶时，计算值与解析值吻合得很好。

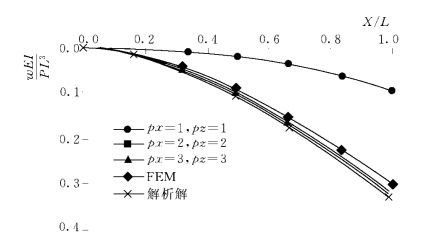
图2-5-14　梁轴线的挠度沿梁长度方向分布曲线

图2-5-15是梁的固端正应力沿梁高度方向分布曲线的计算值与解析值。当块体单元形函数沿X向和Z向取3阶时，计算值与解析值非常吻合。

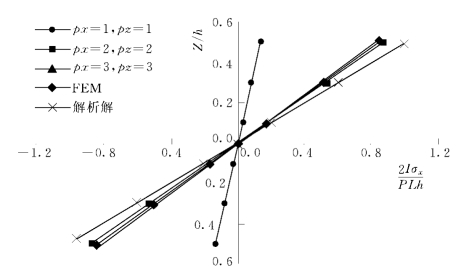
图2-5-15　悬臂梁的固端正应力分布曲线