块体单元法与拱梁分载法的耦合技术

在高山峡谷地区的高坝枢纽建设中，混凝土拱坝是很有竞争力的坝型。中国在建的小湾拱坝和溪洛渡拱坝的高度达300m级，为世界之最。由于工程建设需要的推动，中国在拱坝设计的理论与实践方面，已取得了较大的进展：在坝体的应力、承载力和优化分析方面，传统的拱梁分载法已被推广到弹塑性领域，有限单元法已经在复杂特殊专题的研究中得到广泛使用；在坝肩稳定分析方面，除传统的刚体极限平衡法外，可考虑结构面变形的离散单元法、不连续变形分析法、刚体弹簧元法、块体单元法等现代方法也已经得到逐步推广。

目前，拱坝坝身的应力分析和坝肩的稳定分析大体有两类体系：

（1）首先采用拱梁分载法分析坝身应力并计算坝肩推力，然后结合刚体极限平衡法或其他现代方法进行坝肩稳定校核。优点是计算简单，安全指标有规范可循；缺点是对坝肩岩体渗流和变形性质的假定过多，有一定误差，而且由于将坝身和坝肩分别处理，进行体形优化分析时不太方便。

（2）采用有限单元法或其他现代方法对坝身应力和坝肩稳定同时进行校核。优点是理论上较精确；缺点是计算工作量大，且安全指标尚无规范可循。

为更好地反映拱坝坝身与坝肩岩体的相互作用，笔者研究了块体单元法与拱梁分载法的耦合分析方法（Xu，Chen，2001）。

一、拱梁分载法要点

（一）拱梁分载法的原理

试载法是美国垦务局于20世纪30年代提出的一种方法，当时需通过手工试算求解，所以称为试载法。试载法所需的计算工作量十分浩大，但成果较为合理。目前虽仍沿用试载法这个名称，但实际上系泛指利用拱梁系统变位协调的要求以解算拱坝应力的原理和方法，不再意味着采用试算方式来求拱梁的荷载分配。确切地说，应该改称为拱梁分载法。

试载法就其原理来讲，适用于各种类型的拱坝。试载法通常只给出近似的结果，并不是由于原理上的问题，而是由于在计算中采取了一些近似简化。例如，平面法截面假定、用伏格特公式计算地基变形以及边界条件的近似假定等。

用试载法分析拱坝的基本依据是什么？在力学概念上是否严谨？对这些问题曾有过不同的看法。一些文献通过薄壳理论近似阐述试载法的原理。潘家铮（1981）对这个问题作了较全面的论述，认为试载法虽然将原来完整的结构人为地视为由两套独立的系统组成，而且用类似杆件结构的公式计算两者的变位，再从变位协调条件来确定荷载分配，表面上看似不够严谨，但这种做法是具有明确的力学概念的。如果将拱坝分别切割为拱系及梁系，并且在各切面上施加某种内力系，调整这些内力系，使拱及梁两套系统在外载和内力系作用下，变位处处一致，则根据弹性力学中唯一解原理可知，其所加的内力系一定代表切割面上真正应力的影响，所求出的拱梁应力及变位就是拱坝的真实解答。

为充分简化计算工作以达到实用的程度，在试载法中计算拱和梁的变位时，采用了一个基本假定：拱的法向截面在变形后维持为平面。这个假定相当于壳体理论中的法截面维持平面假定或杆件系统中的正截面维持平面假定。拱坝中的拱和梁，不是一根独立的杆件，而是从空间结构中切取的一片，处于三向应力状态。严格地说，其变位公式与独立的杆件有所不同（如存在泊松比影响，而独立杆件就无此问题），应该另行推导。但是，进一步分析后可以发现，忽略一些次要因素后，拱坝中拱梁变位的计算公式和相应杆件的公式基本一致，所以可以直接用材料力学公式计算拱、梁变位。如要深入研究某些问题，则须注意到上述区别。例如，计算梁的扭转时，扭转刚度采用2EI，便是考虑到梁是从连续壳体中切取的一个截条，而不是一根普通的悬臂梁。

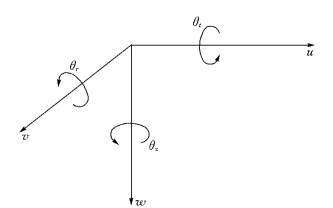
图2-5-1　点的6个变位

试载法通过拱和梁在同一点上变位协调条件来解算拱和梁所承受的荷载。一点上的变位有6个分量（图2-5-1）：3个线变位u（切向）、v（径向）、w（竖向）和3个转动角θz（绕z轴的水平扭角）、θt（绕t轴或x轴的垂直扭角）、θr（绕r轴或y轴的垂直扭角）。相应地，在拱或梁上的荷载也有6种：径向荷载p、切向荷载q、竖向荷载s、水平扭载m z、竖向扭载mt及m r。因此，从最完整的角度讲，应设置6个未知的内力函数，且通过每个结点上6个变位分量的协调条件来建立方程，以确定未知值，即所谓六向全调整。但一般地，只需进行三向调整便可获得问题的解答。通常选取以下3种荷载为独立变量：①径向荷载p；②切向荷载q；③水平扭载mz。变位协调条件也仅核算相应的3个：①径向变位v；②切向变位u；③水平转角θz。

必须强调的是：仅选用p、q、mz为未知量，并不意味着在拱和梁上仅需施加这3种荷载，恰巧相反，在拱和梁上必须施加全部6种荷载，只不过另外3种荷载可以用p、q、mz表示而已。同样，在计算3种变位v、u、θz时，必须计算出在6种荷载作用下的这些变位，并非只计算在p、q、mz作用下的这些变位。由此可见，采用三向调整，未知元素数量虽少了，计算步骤则要曲折一些，这是因为在计算变位时，要计及另外3种荷载的影响，而这另外3种荷载又须设法用选定的3种荷载来表示。在许多实际问题中，那些被视为非独立量的荷载s、mt、mr中的一部分对需核算的变位分量v、u、θz并无影响，或影响很小，可以忽略，不必全部计及，从而使三向调整大为简化。但应注意，这些非独立变量中至少有一部分的影响是不能忽略的。对于某些拱坝（如薄双曲拱坝），甚至全部不能忽略；对于一般的拱坝，只有垂直扭载mt对梁变位的影响不能忽略，其余均可不计。故采用三向调整分析一般的拱坝时，仅当计算悬臂梁的各种变形时，需同时考虑p、q、mz和mt四者的影响。

要在计算中考虑m t的影响，可以先将m t以m z表示，也可采用迭代法解算，即将垂直扭载的影响作为迭代修正项处理。或者采用吉林大学数学系提出的2m法，就是说，垂直扭矩的影响可以用拱上水平扭矩乘以2来代替。最根本的方法是直接将mt作为独立变量，相应增加垂直扭转角的变位协调条件，这就变为四向调整，计算量增大。无论采用何种方法，都应该得到相同的解答。当需要更精确地考虑各种次要影响时，如仍采用三向或四向调整，则会不够方便，此时宜采用五向调整。

（二）拱梁杆件的分析

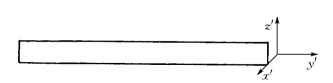
图2-5-2　拱梁杆件的坐标规定

从本质上说，拱梁杆件属于同一类构件，只不过一个曲率大，一个曲率小。在网格划分较密时，它们之间的差别很小，都可以认为是直杆。因此，为简单起见，可同等看待。如图2-5-2所示，拱梁杆件的每端有6个位移，对应的自由度为[x′ y′ z′ θ′x θ′y θ′z]T，相应的力为[Q′ N Q M T 0]T，其中，Q′、N、Q、M、T依次为切向剪力、轴力、剪力、弯矩和扭矩，0表示侧向无矩。

1.刚度矩阵

内力与位移的关系为

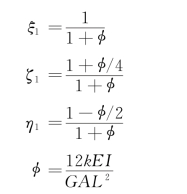
式中：ξ1、ζ1、η1和φ为考虑剪切影响的修正系数；E为弹性模量；G为剪切模量；L为杆件长度；A为杆件截面面积；I为截面惯性矩；k为考虑截面形状的不均匀系数。

2.荷载计算

（1）均布轴力[图2-5-3（a）]。

（2）三角形分布轴力[图2-5-3（b）]。

（3）均布剪力[图2-5-3（c）]。

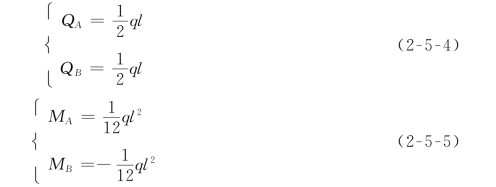
（4）三角形分布剪力[图2-5-3（d）]。

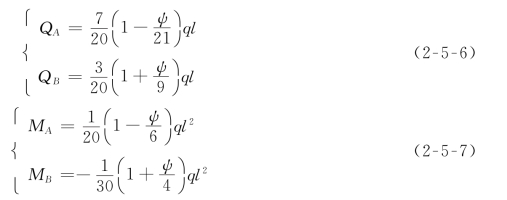
其中

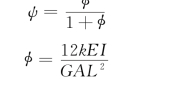
（5）均匀温升ΔT。

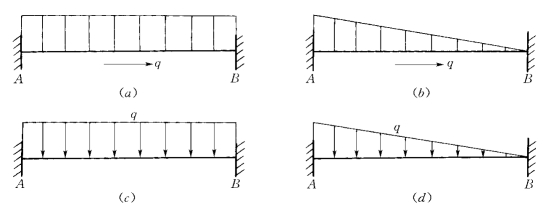
图2-5-3　荷载分布

（a）均布轴力；（b）三角形分布轴力；（c）均布剪力；（d）三角形分布剪力

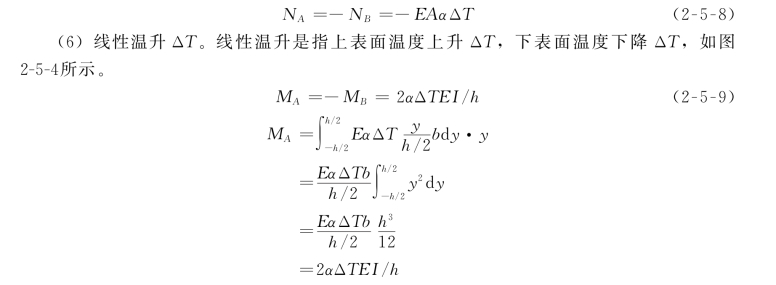
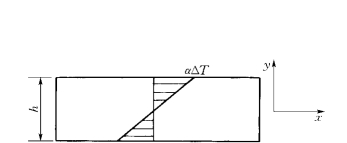
图2-5-4　线性温升

图2-5-5　拱梁单元

3.应力计算

（三）拱梁的整体分析

1.单元规定

式中：[H]a和[H]b分别为从角点位移到拱向和梁向位移（相邻角点的平均值）的转换矩阵。

再将拱向位移和梁向位移转换到拱或梁的局部坐标系，即

式中：[T]a和[T]b分别为整体坐标系到拱或梁局部坐标系的位移转换矩阵。根据所规定的局部坐标的方向，有

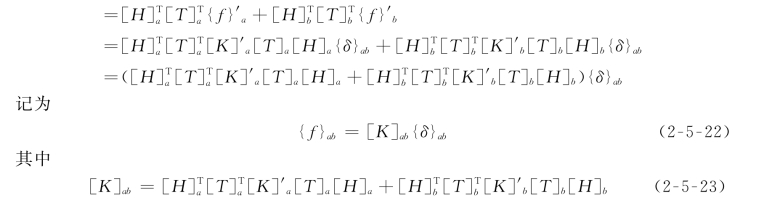
式（2-5-23）即为整体坐标系下的平衡方程。

从更准确的角度来说，拱向和梁向不应只用等效的一条拱或梁来代替，而应划分为无数的拱或梁，将拱向的所有拱片进行积分，才是真正的等效拱，将梁向的所有梁片进行积分，才能更准确地表示梁的作用，如图2-5-6所示。

以拱向为例，对一条微拱段，两端的结点位移用拱梁单元的角点位移来表示，即

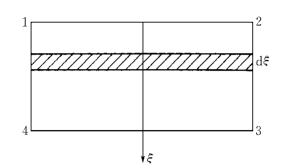
图2-5-6　拱向积分示意图

(www.xing528.com)

式（2-5-26）是一个拱片转换成的刚度矩阵，积分后即得到整体拱的作用。由于在拱片的刚度系数表达式中，无论是面积A还是惯性矩I都是dξ的线性函数，即

因此，最后的刚度系数中只是多了一项积分表达式，而其余部分则是整条拱的对应刚度系数。可以看出，这些积分表达式只有两种取值，即

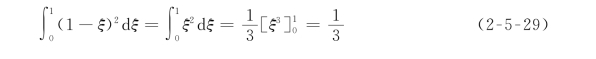
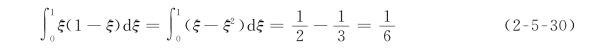
直观地，可以先计算整条拱的刚度系数，然后将它们分配到各个结点上。若位移是自身结点引起的，则分配系数为1/3；若位移是由邻边结点引起的，则分配系数为1/6。

在计算荷载时，可以把总荷载都加在梁上或拱上，这与把一部分荷载加在拱上、一部分荷载加在梁上，作用是等效的。因为根据位移协调的关系，它们之间的荷载会自行调节。需要注意的是，温度荷载对拱向和梁向都同时作用，因此需要同时施加，实际上就是拱向和梁向都同时变形。

二、耦合分析

（一）拱坝网格的自动剖分

1.拱坝体形

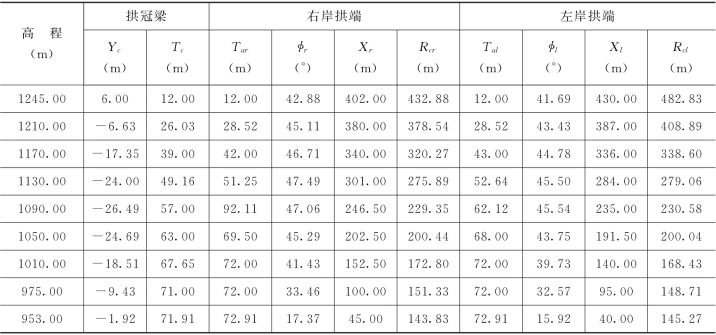
以小湾抛物线双曲拱坝为例。该拱坝轴线方位角为S178°E，坝顶原点大地坐标为X=36863.00，Y=13416.00。拱坝的体形参数见表2-5-1，拱冠梁剖面见图2-5-7，平面拱圈见图2-5-8。

表2-5-1　小湾抛物线双曲拱坝体形参数

平面拱圈中轴方程为

式中：Rc为拱圈曲率半径（Rcr表示右拱圈曲率半径，Rcl表示左拱圈曲率半径）；φi为拱圈半中心角（φr表示右拱圈半中心角，φl表示左拱圈半中心角）。

平面拱圈厚度沿弧长变化公式为

式中：Ti为i（X i，Y i）点厚度；T c为拱冠梁厚度；T ai为拱端厚度（T ar为右拱端厚度，T al为左拱端厚度）；Si为i（X i，Y i）点中心线弧长；S为左拱或右拱中心线弧长。

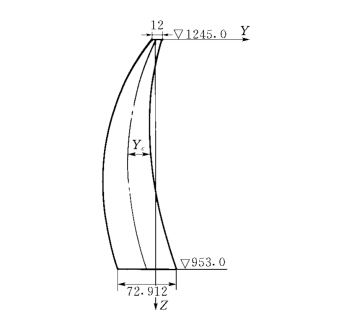
图2-5-7　拱冠梁剖面示意图（单位：m）

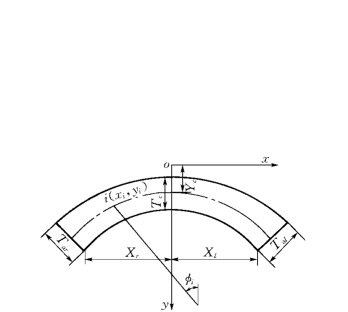
图2-5-8　平面拱圈坐标计算示意图

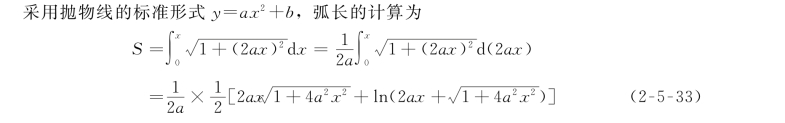
求总弧长时，积分到拱端；求到某一点的弧长时，积分到该点即可。

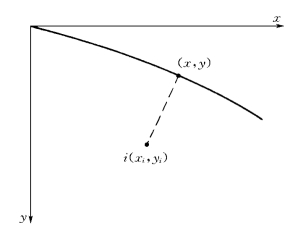
图2-5-9　求抛物线法线交点示意图

2.网格剖分基本流程

沿拱圈的中心线每隔一段弧长取一点，从该点作法线与上下游坝面相交，即可将该拱圈离散。为了使各拱圈在立面上一致，可先取一系列参考点，然后作到每一拱圈的法线，求出与中心点的交点（图2-5-9）。

从抛物线外一点作到抛物线的法线，交点（x，y）需满足方程

即

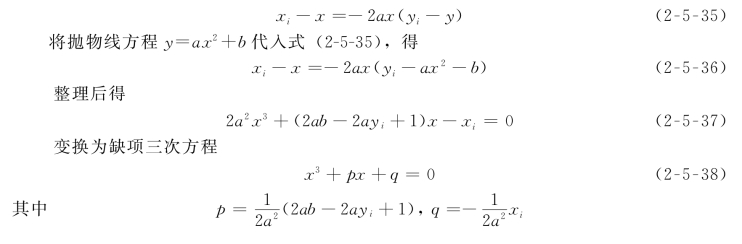
取第一个实根x 1=A+B即可。

求得法线与中心线的交点后，沿此法线前后延伸该点的半个拱圈厚度，就得到上下游面的交点。由不同的参考点可得到相应的该拱圈的上下游交点。对每层拱圈都照此处理，就能离散出全部结点。

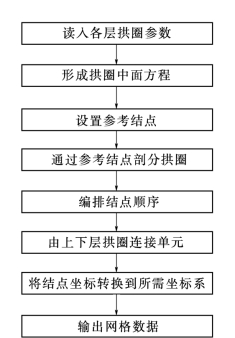
图2-5-10　拱坝网格剖分流程图

参考点的选取可根据网格疏密确定，为简单起见，可取为每层拱圈的端点。若要加密网格，只需插值定出更多的拱圈就可以了。

单元的连接则根据上下层拱圈的对应关系，从中心向外顺次形成。注意到下层拱圈比上层拱圈结点少，所以在边界部位下层拱圈的结点有重合，单元呈退化情况。另外，对坝体的左半部分和右半部分连接单元时，由于都是从中心向外扩展，故有一半单元的结点顺序是相反的，需要在最后把次序变换过来，使输出的单元格式一致，即先是下游面结点的顺时针编号，然后是上游面结点的顺时针编号（从下游面看）。

图2-5-10是拱坝网格剖分流程图。

（二）拱梁单元和块体单元连接信息的形成

为了获得块体单元系统和拱梁单元系统耦合的信息，需知道拱梁单元系统的基础结点落在哪一个块体单元上。由于块体单元很多，又没有固定的顺序，因此人工查找十分困难。为此需通过计算来判断基础结点的归属。

（三）拱梁单元和块体单元的耦合

假设拱梁单元系统的基础结点固接在块体单元表面上，块体单元的位移和基础结点的位移存在一定的关系。只要把基础结点的位移自由度消去，把拱梁单元的刚度叠加到块体单元的刚度上，就可以完成拱梁单元和块体单元的耦合。

1.刚度的平移变换

首先讨论如何把单元刚度矩阵从i点变换到j点。设i点和j点都固接在同一刚体上，则i点的位移可用j点的位移表示为

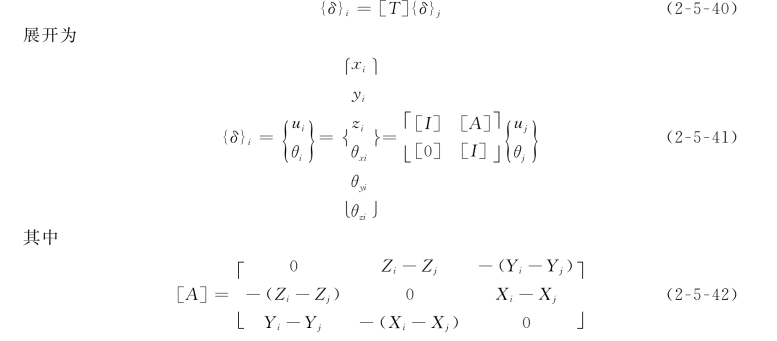
i点的结点力与j点的结点力变换关系可表示为

原来的结点力和结点位移的关系为

将转换关系式（2-5-43）和式（2-5-40）代入式（2-5-44），得

因此，转换后的刚度矩阵为

2.拱梁单元和块体单元的耦合变换

为将拱梁单元的刚度矩阵[K]ab转换为与块体单元形心位移{U}rl对应的刚度矩阵，可先写出拱梁单元的刚度方程，即

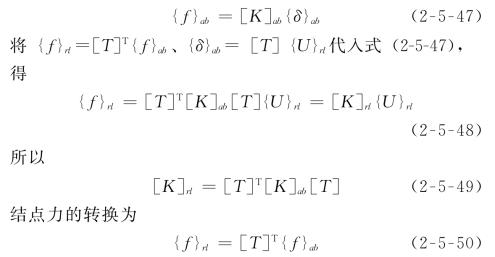
与地基相连的拱梁单元经过转换后，基础结点的自由度被消去，对应的方程变成了与块体单元自由度相关的方程，这时基础拱梁单元既与块体单元相关，又与坝体内部结点相关。将刚度矩阵组装在一起，就可以完成拱梁单元和块体单元之间的耦合分析。

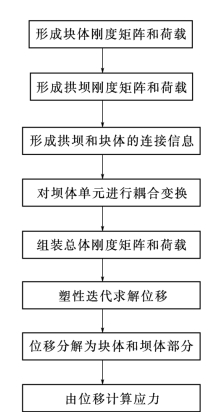
图2-5-11　耦合分析流程图

以上计算过程可用图2-5-11所示流程图表示。