阶谱块体单元法在连续介质中的优化应用建议

阶谱块体单元法从本质上来说是一种不连续介质力学方法。实际上，岩体介质的连续与不连续之间并没有绝对的分界线。Muller（1974）主张用主应力比效应判断介质的连续性，并提出以σ1=（4～5）σ3作为连续介质和非连续介质的分界线。但也有学者认为，介质的连续或不连续不是理论上的问题，而是一个实践上的问题（薛守义，1999）。一方面，在岩土工程问题中常遇到的介质，其力学性质的变化往往是连续的，例如，随着岩体从地表的强风化向深部逐渐变化到弱风化、微风化和新鲜岩体，岩体的力学参数也逐渐过渡变化。另一方面，在数值模拟研究中，不可能过细地分区或分带，而必须作适当的区段划分，分别选取力学参数。在不同区段的交界面上，介质变成了不连续的。此外，在岩体中广泛存在着节理、断层等结构面，在结构面两侧，岩体具有产生非连续变形的可能性。可见，岩体往往既有非连续性，又有连续性。因此，当用数值方法来模拟岩体时，不论是连续介质力学方法还是不连续介质力学方法，都应该具有模拟两种变形行为的能力（李永明，汪卫明，陈胜宏，2002）。

本节讨论用不连续介质力学方法模拟连续介质力学行为的问题，其中的关键是虚拟结构面的处理。

一、虚拟结构面的处理方法

1.不连续变形分析法（DDA）的处理方法

不连续变形分析法把结构面看作是块体之间的接触面，接触面的力学性质通过设置于接触点上的弹簧系数来反映。块体之间在力学上的连续性取决于结构面的变形条件：当结构面受力超过允许强度时，结构面发生滑动或开裂，此时岩体呈现不连续性；当结构面受力不超过允许强度时，结构面不发生滑动或开裂，此时岩体呈现连续性。块体系统非连续特性主要表现为块体间的接触面是非连续的，并且通过接触面的相互约束建立整个系统的力的平衡（裴觉民，吕祖珩，1996）。

在应用于连续介质问题或者不连续介质问题中的连续区域时，可以采用有限单元法的耦合分析方法（郑榕明，张勇慧，王可钧，2000），也可以采用把块体进一步细分的方法（吴洪词，1996）。Cheng&Zhang（2000）认为，虽然块体的内部离散可以是有限单元离散或DDA块体离散，但由于有限单元法和DDA的概念完全不同，从而算法和程序编制复杂而难以实现，为此，他们提出了一种内部离散的算法，并通过引入内部弹簧以保证每个块体的连续性。

2.离散单元法（DEM）的处理方法

在离散单元法中，岩块本身被视为刚体或变形体，岩块的表面可以发生变形。当前块体对与其相邻块体之间没有连续性的要求，即块体的运动没有变形协调问题，每个块体只是根据其受力的大小按牛顿定律运动，甚至可以与母体分离。岩块的运动使邻接面由接触变为分离或嵌入，接触点处的法向作用力或切向作用力的增量与嵌入量（或脱离量）之间为线性关系，比例系数即为法向刚度系数和切向刚度系数。根据法向作用力为拉力或压力以及切向作用力与摩擦力的相对大小关系确定块体之间是拉开还是接触以及在接触时是否有热能产生，如果有热能产生，这部分能量由一个与法向刚度和切向刚度并联的阻尼器贮存。阻尼力与速度成正比，比例系数为阻尼系数。有研究者认为，离散单元法缺乏理论的严密性，计算中力系不能完全平衡，精度较差，主要适用于应力水平不高的情况。

日本学者在对DEM的有关计算参数进行研究后建议：法向刚度系数k n的取值可等于岩体的弹性模量E，切向刚度系数ks等于法向刚度系数k n乘以一个0～1之间的折减系数s，并建议s=0.25；阻尼器的法向粘滞系数ηn在法向刚度系数k n上乘以一个比例阻尼系数β得到，而切向粘滞系数ηs等于法向粘滞系数乘以s；摩擦系数则由试验确定。

3.数值流形方法（NMM）的处理方法

在数值流形方法中，结构面总是成为流形单元的边界。把个别不连续边界连接成一个系统，材料变形时不连续边界的移动满足在两接触边之间无拉力和无嵌入的条件。在寻找接触时，用弹簧计算不连续变形，通过适当选择接触弹簧的刚度以保证在嵌入判断和嵌入锁定时开合迭代的收敛。

石根华认为（1997），对于连续介质问题，当接触弹簧的刚度取为弹性模量的20～200倍时是合理的。

蔡永昌等研究了数值流形方法在连续介质体中的应用（蔡永昌，张湘伟，骆少明，1999）。他们采用重叠的数学网格和物理网格计算无裂缝的连续体，用Hammer积分代替数值流形方法中常用的单纯形积分，以解决为了提高计算精度而采用高阶位移函数带来的单纯形积分困难。

也有不少研究者认为，对这种不真实的结构面应该采用与块体自身相当的材料参数（任青文，1995）。

4.块体单元法（BEM）的处理方法

在阶谱块体单元法中，块体单元的位移场以多项式（完全的或不完全的）基函数来近似，而结构面的变形以结构面上某点处两侧面的法向和切向位移之差来描述。假定结构面中沿厚度方向的应变是相同的，并忽略沿结构面延展方向的正应变和正应力，即可提出简单的本构关系以确定结构面的法向正应力和切向剪应力与相对变形之间的关系。对结构面赋予适当的本构关系后就可以处理岩体结构中结构面以及岩块之间的滑移、拉裂、闭合、接触等非线性力学行为。结构面上的变形通过施加法向和切向刚度来进行考虑。与其他几种基于点接触假定的方法不同的是，接触弹簧只与接触点对应，而在弹粘塑性块体单元理论中，法向和切向刚度分布于结构面上。

阶谱块体单元法由于可以考虑块体单元的变形，且数值稳定性好而具有吸引力。岩体中由结构面切割而成的块体单元大小不一，如果把它们同等对待会导致不同块体单元的计算结果精度不匹配。阶谱块体单元法可以通过提高形函数阶次来提高精度。不过，还有另外一种同样简单的方法可以使尺度大的块体单元获得和尺度小的块体单元相当的计算精度，即通过引入假想的结构面对尺度过大的块体单元进一步细分。笔者结合算例对此问题进行了数值计算研究（李永明，汪卫明，陈胜宏，2002）。

二、算例考核

图2-4-10　受拉伸的板

考察一个单边受拉的L形板（图2-4-10），厚度为1m。不考虑自重，且仅作弹性计算。对厚度方向的前后两个表面施加Y方向的约束，使它成为一个平面应变问题。块体的计算参数为：弹性模量E=20GPa，泊松比μ=0.18。虚拟结构面的计算参数为：法向刚度系数k n=3000GPa/m，切向刚度系数ks=1500GPa/m。

1.计算精度控制

分别用有限单元法和阶谱块体单元法对该算例进行弹性计算。有限单元法分别采用两套网格来计算：粗网格由192个均匀划分的六面体等参单元构成，结点数为450；细网格由3072个六面体等参单元构成，结点数为6402。阶谱块体单元法计算时，先将结构划分为两个块体单元[图2-4-11（a）]，两个块体单元通过虚拟结构面AB相邻。(www.xing528.com)

为了比较块体单元法中不同阶次的计算结果，计算了7种阶次的情况，即X和Z方向的阶次分别取1～7，计算结果如表2-4-6所示。表中的相对误差是指由块体单元法和细网格有限单元法计算的位移增量之间的相对差值。

图2-4-11　不同的分块方案

（a）2块体单元方案；（b）3块体单元方案；（c）4块体单元方案；（d）8块体单元方案；（e）直8块体单元方案；（f）斜8块体单元方案

由表2-4-6可见，阶次越高，精度也越高，但由于相应的广义自由度数增加，使得计算时间也随之增加。在凸角点（即A点），仅仅使用两个块体单元且在X和Z方向分别取4阶，块体单元法结果即与有限单元法细网格的结果非常接近。在凹角点（即B点），块体单元法在X方向的位移分量增量结果与有限单元法的结果比较吻合；随着阶次的升高，Z方向位移分量增量也逐步向有限单元法的结果逼近，但直到7阶时，块体单元法在Z方向位移分量增量与有限单元法结果仍有一定的差距，从而导致B点的位移增量误差范数比A点大。由于A点正好是覆盖单元的结点，B点则位于覆盖单元的1条棱边上，B点的X坐标与覆盖单元棱边上各点的X坐标相同，根据A点3个位移分量增量和B点X方向的位移分量增量精度较高这一事实，可以得出结论：在越靠近覆盖单元结点的部位，计算精度越高。

表2-4-6　块体单元法和有限单元法计算结果的比较（2块体单元方案）

2.分块方案的影响

为了研究单元形状和单元密度对计算结果的影响，将L形板结构分别划分为1、2、3、4、8个块体单元进行计算。其中，1块体单元方案是没有虚拟结构面的情形；2、3、4、8块体单元方案的块体单元划分情况如图2-4-11所示。计算结果见表2-4-7。

表2-4-7　不同单元划分方案计算结果的比较

从表2-4-7可以看出，随着单元数的增加，位移向有限单元法的结果趋近。其中，3块体单元方案和直8块体单元方案各个块体单元的每一个顶点都是覆盖单元的结点。比较8块体单元的3种单元划分方案的4阶计算结果，可以看出，单元为长方体时（直8块体单元方案），计算时间及计算精度都明显优于另外两种方案；当单元形状发生歪斜后（斜8块体单元方案），计算时间增加了3倍多，计算精度也有所下降。这说明计算时间和计算精度对于单元形状敏感。上述事实再次说明，在越靠近覆盖单元结点的部位，计算精度越高。由此可见，虽然覆盖单元是规则的长方体单元，但块体单元的形状对计算结果尤其是计算时间有一定的影响。此外，单元密度对计算精度也有影响。

综上所述，要提高块体单元法的精度，应从以下三方面入手：

（1）使单元的形状尽量接近于长方体。

（2）通过p型自适应技术，提高插值函数的阶次。

（3）通过h型自适应技术，加密块体单元网格。

3.虚拟结构面上材料参数的合理取值

在阶谱块体单元法中，通过改变虚拟结构面的数量和位置，块体单元的数目和形状是可以改变的。然而，虚拟结构面并非材料原来所具有，在添加了虚拟结构面后，位移协调性遭到了破坏。因此，应有足够大的刚度系数kn和ks，以消除虚拟结构面对计算结果的影响。

对于虚拟结构面的材料参数如何取值才比较合适的问题，需要进行专项研究。强天驰等人曾经为了解决有限单元法中相邻结点密度相差较大时交界面上相应结点的位移和应变不协调的问题，提出过一种用界面过渡单元来耦合网格的方法，将有限单元疏密网格之间的界面刚度耦合到总刚中，可以保证该界面两侧各相应点上的位移和应变在界面上协调。他们对界面虚拟弹簧刚度系数作了研究和推导（强天驰，寇晓东，周维垣，2000），推导的最终结果依赖于一个经验常数c。

笔者采用2块体单元和8块体单元方案（图2-4-11），并使结构面上法向刚度系数kn和切向刚度系数k s保持一定的比例协调关系，而k n/E逐渐增大，考察某些点上虚拟结构面两侧位移的差值，计算结果见表2-4-8。表中的相对误差是指在虚拟结构面两侧有相同坐标的点的位移差值。

表2-4-8　不同k n/E值下虚拟结构面两侧位移之差

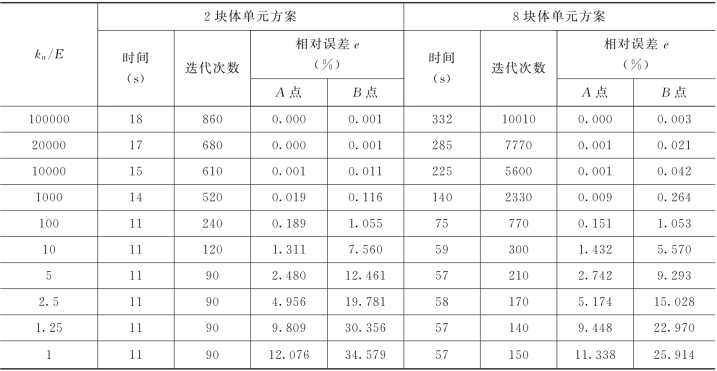
由表2-4-8可见，k n/E越大，计算时间越长。此外，计算时间也与单元数目有关。kn/E与相对误差e之间并非简单的线性关系，当kn/E较小时，随着k n/E增大，误差逐渐减小，但当kn/E增大到一定值以后，问题不能收敛到正确解。表2-4-8中所列的是误差尚未“反弹”且保证收敛时的结果。根据笔者的研究，当k n/E值在100～20000之间时，可以保证相对误差约在0.02%～1.05%之间。因此，笔者建议，当块体单元数目不超过10，且基函数阶次不超过4阶时，k n/E可取为100～20000；当块体单元数目多于10或基函数阶次高于4阶时，kn/E可参照此值选取。