建立阶谱块体单元法的优化方法

本章第二节提出了一种广义弹粘塑性块体单元法的初步构想，理论不复杂，编程较简单，算例也表明了该方法的有效性。但进一步的研究却发现，该方法有两个重大缺陷：

（1）直接采用任意高阶多项式拟合位移场，联立方程求解的是系数向量，其量值与坐标系有关，稳定性差。实际上，当多项式阶数高于3时，求解已很困难。

（2）很难实现多项式阶数的自适应调整。

本节将采用稳定性较好的阶谱形函数，并进一步考虑岩石块体单元的屈服，建立一种阶谱块体单元法（Wang，Chen，2001）。形函数的阶谱特性还将为以后自适应块体单元法的发展打下坚实的基础。

阶谱块体单元法的名称来源于升阶谱有限单元法（又称为p型有限单元法）。阶谱是指块体单元的位移插值函数是阶谱插值函数，由此推导出的刚度矩阵、质量矩阵、荷载向量以及自由度向量也具有阶谱特性。在有限单元法中，引入阶谱插值函数或进一步细分单元的目的都是为了提高求解精度，它们分别被称为p型和h型方法。p型方法在很多椭圆型线性问题中已被证明是非常有效的。对于Poisson方程、Lamé方程、Reissner-Mindlin问题等，p型方法优于h型方法。如果网格设计合理，p型方法能够以能量范数的指数速度收敛于精确解（Düster，Bröker，Rank，2001）。

阶谱块体单元法通过引入覆盖单元并采用阶谱形函数来描述一个覆盖单元内的位移场，根据所假设的覆盖单元位移模式建立平衡方程、几何方程和本构方程，通过求解平衡方程组得到问题的近似解。由于引入了结构面和块体单元的弹粘塑性本构关系，因此可以同时考虑结构面和岩石块体单元的屈服和时间效应。该方法前处理过程简单，精度较高，而且可以推广应用到连续介质力学问题中去（李永明，汪卫明，陈胜宏，2002）。

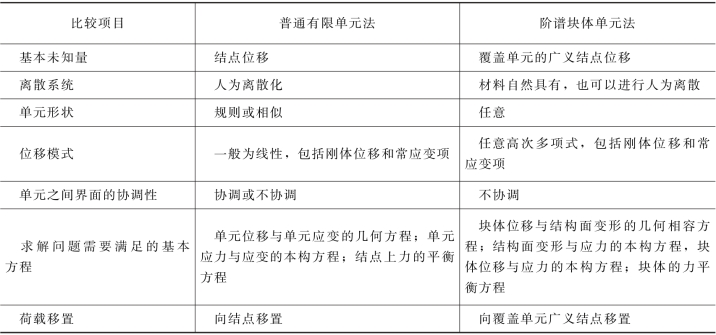
为了明确阶谱块体单元法的有关概念，表2-4-5从某些侧面对阶谱块体单元法与普通有限单元法进行了比较。

表2-4-5　阶谱块体单元法与普通有限单元法的比较

一、基本原理

1.覆盖单元

阶谱块体单元法将岩体视为由结构面和被结构面切割而形成的岩石块体单元的组合。每个任意形状的块体被视为一个单元，各块体单元通过结构面互相联系，各块体单元之间的接触假定为面接触。由于块体单元形状不规则，要直接描述块体单元内部的变形比较困难，因此，在阶谱块体单元法中引入了覆盖单元的概念。覆盖单元在几何上是一个能够把块体单元完全包围的长方体（图2-4-5），在力学上它是一个有限单元，而且它是块体单元的进一步延伸，即块体单元内任意点的力学量可在覆盖单元内插值得到。从理论上来说，只要能够描述其内的位移场，覆盖单元可以是任何方便的单元类型，可以具有任何方便的形状（如圆形、三角形和矩形等），但是选择某些类型的覆盖单元可以使计算更为方便。笔者采用了长方体有限单元作为覆盖单元。

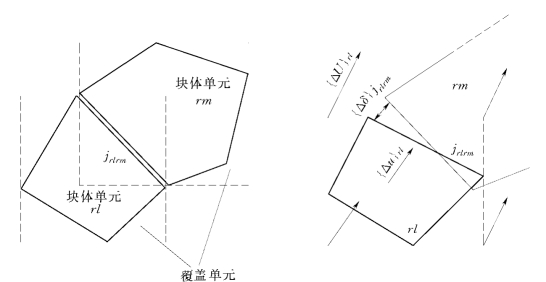
图2-4-5　覆盖单元及其广义位移增量

在阶谱块体单元法中，覆盖单元和块体单元是一一对应的，一个覆盖单元只覆盖一个块体单元且完全覆盖了这个块体单元，块体单元总是其覆盖单元的子域，且不同块体单元的覆盖单元虽然可以重叠但彼此没有直接联系，真正联系不同块体单元及它们的覆盖单元的还是块体单元之间的结构面。因此，在一个块体单元中位移函数是连续的，但不同块体单元的位移函数是不连续的，从而体现了结构的不连续特性。

2.位移函数

有了覆盖单元以后，就可以采用有限单元法中描述单元位移模式的办法来描述覆盖单元的位移场。和p型有限单元法类似，阶谱块体单元法的覆盖单元是由常规的位移协调元结合数量逐渐增加的附加自由度而构成的。这些附加自由度以不违反位移连续条件的逐次升幂多项式函数作为基函数。如果在安排自由度时使得低阶单元的自由度是高阶单元的自由度的一个子集，那么，低阶单元的刚度矩阵、质量矩阵、荷载向量是同一问题的高阶单元相应矩阵的子阵。当基函数的最高阶次等于1时，覆盖单元就是通常的长方体有限单元；当基函数的最高阶次高于1时，基函数中的高阶项将对单元贡献广义的自由度，可以被看作是虚结点的自由度。虚结点和实结点统称为广义结点。由于覆盖单元是一个规则的长方体，因此在有限单元法中的所有高阶六面体等参单元和p型有限单元法中的所有可能的基函数在这里都可以采用。笔者采用基于标准Legendre多项式的Serendipity族函数（程昭，陈胜宏，1999）作为块体单元的覆盖单元的基函数。Serendipity函数的阶谱特征和更好的数值稳定性对于进一步研究p型自适应很重要。Serendipity族函数由点基函数、棱基函数、面基函数和体基函数组成，其具体表达见式（1-8-51）～式（1-8-71）。

式中：[N]rl为形函数矩阵，其具体形式由单元位移函数的阶次p决定；f rl（p）为广义自由度的个数；φi为点基函数、棱基函数、面基函数和体基函数的统一记号；[I]为3阶单位阵；{ΔU}rl为覆盖单元上相应于广义结点的广义位移增量矢量。

3.几何方程

第rl个块体单元的应变增量为

式中：[B]rl为应变矩阵，其元素由基函数对坐标的导数组成。

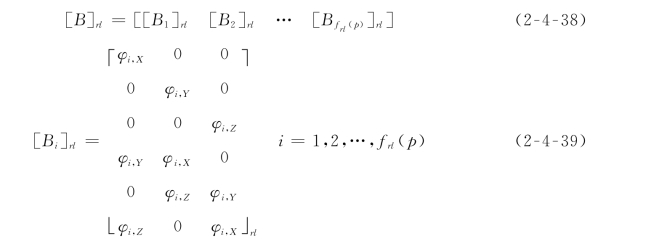
由于基函数的阶谱特性，应变矩阵也是阶谱形式。

如果块体单元rl和rm通过结构面j rlrm相邻，则块体单元rl和rm的位移增量将在结构面j rlrm两侧的岩体引起相对变形增量{Δδ}jrlrm，应用运动学原理可推出它们的关系为rlrmrlrm

式中：[L]jrlrm为由整体坐标到局部坐标的转换矩阵，可由结构面j rlrm的倾向和倾角确定[式（2-2-20）]；函数J（j rlrm）的定义见式（2-2-24）。

4.本构方程

（1）岩石块体单元。采用显式时步离散（Owen，Hinton，1980），第rl个块体单元内的应力增量和应变增量之间的关系可以表示为

式中：φ、c分别为块体单元的内摩擦角和凝聚力。(www.xing528.com)

（2）结构面。第jrlrm个结构面上任意点的应力增量和变形增量之间的本构关系见式（2-4-8）～式（2-4-12）。

5.平衡方程

由虚功原理可推导出块体单元系统的平衡方程为

式中：[K]为整体广义刚度矩阵，由单元广义刚度矩阵组合而成；{ΔU}为整体广义位移增量向量；{ΔF}为整体广义荷载增量列阵。

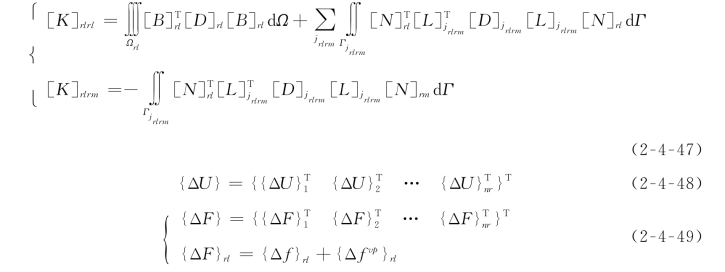
式（2-4-47）的第一式中，右端第一项是块体单元rl对自身刚度的贡献，右端第二项是块体单元rl周围各结构面j rlrm对该块体单元刚度的贡献；式（2-4-47）的第二式为块体单元rl周边各块体单元rm对该块体单元刚度的贡献，rm与rl通过结构面j rlrm接触。

式（2-4-49）中，{Δf}rl为外荷载向量；{Δf vp}rl为由块体单元rl及其周围各结构面j rlrm上的粘塑性应力转化来的等效广义荷载向量，有

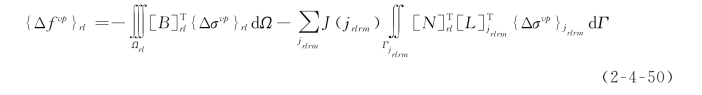
求解方程组（2-4-46），可以得到覆盖单元的整体广义位移增量向量。由式（2-4-36）、式（2-4-40）、式（2-4-37）、式（2-4-41）和式（2-4-8），可以分别得到块体单元内部和结构面上的位移增量向量、应变增量向量和应力增量向量。

6.广义荷载移置

由块体单元和结构面的粘塑性变形产生的等效广义粘塑性荷载增量{Δf vp}rl由式（2-4-50）给出，作用于结构物上的广义外荷增量的移置由式（2-4-33）～式（2-4-35）给出。

二、算法实现

阶谱块体单元法与p型有限单元法有很多类似的地方（程昭，陈胜宏，1999）。

1.刚度矩阵和荷载向量的形成

在阶谱块体单元法中，可以仿照有限单元法形成总体刚度矩阵和荷载向量。如果某个块体单元rm通过块体单元rl的某个结构面j rlrm与块体单元rl相邻，把rm对rl的单元刚度的贡献加到rl的单元刚度里面，即得到块体单元rl的各广义结点处的总刚度。荷载向量的形成也遵循同样的原则。可以一边计算单元特性矩阵，一边将其元素组装到总体刚度矩阵中，形成总体刚度矩阵，当然也可以在形成单元刚度矩阵以后进行组装。由于块体单元编号的任意性，所形成的刚度矩阵不具有带状的性质。

2.数值积分

式（2-4-47）和式（2-4-50）中出现了面积分和体积分，可以采用本篇第二章第四节介绍的数值积分方法进行计算。

3.边界条件处理

一般情况下，边界位移约束条件可以当作面约束（法向约束或全约束）来处理。这时，只需给约束面一个合理的罚刚度系数，并将式（2-4-47）中的求和下标jrlrm对块体单元rl的各约束面循环，即可在整体平衡方程中考虑约束面的影响。例如，对于全约束，法向和切向罚刚度系数都应取得很大；对于法向约束，法向罚刚度系数应取得很大，而切向罚刚度系数应取得很小。这种方法简单有效，但是约束面罚刚度系数的取值不易把握。罚刚度系数取值偏小会影响计算精度，取值偏大又可能引起整体平衡方程病态。关于罚刚度系数的合理取值问题，可参照本章第四节中关于虚拟结构面参数取值的讨论。

如果边界面与整体坐标轴垂直，即块体单元与其覆盖单元的边界面重合，则可以将块体单元的边界条件转化成其覆盖单元的边界条件来进行处理，以避免罚刚度系数对计算结果的影响。此时，只需将覆盖单元上与块体单元约束面对应的点、线、面等广义结点在该方向上进行约束即可。从形函数的表达式可以看出，受约束的点、线、面形函数在约束方向上总是一次的，在其他方向上才有高次项。

三、算例考察

仍对图2-4-3所示的重力坝剖面进行分析。在阶谱弹粘塑性块体单元法的计算中，沿X和Z方向均取5阶形函数，沿Y方向取1阶形函数。在弹粘塑性有限单元法的计算中，共划分904个单元。图2-4-6和图2-4-7分别是用两种方法计算出的X—Z断面的位移场，图2-4-8和图2-4-9分别是用两种方法计算出的X—Z断面的主应力矢量。可以看出，阶谱弹粘塑性块体单元法计算的结果与弹粘塑性有限单元法计算的结果吻合得很好。

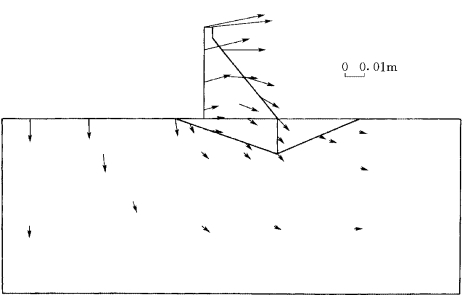
图2-4-6　阶谱弹粘塑性块体单元法计算的位移场

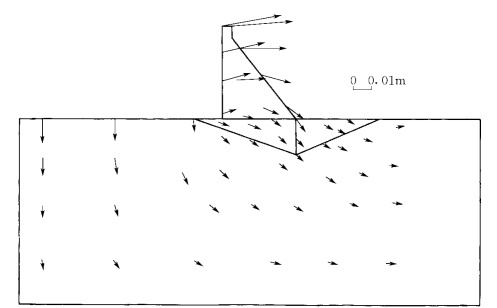
图2-4-7　弹粘塑性有限单元法计算的位移场

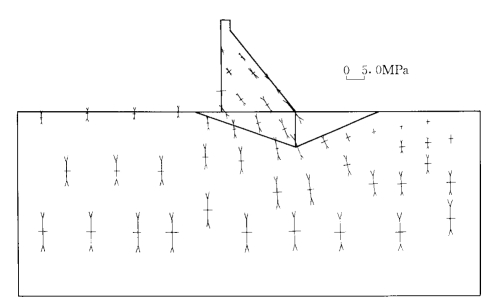
图2-4-8　阶谱弹粘塑性块体单元法计算的主应力矢量

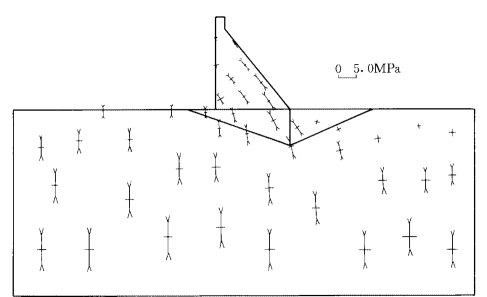
图2-4-9　弹粘塑性有限单元法计算的主应力矢量