计算岩体力学与工程：基本理论模型

虽然常规弹粘塑性块体单元法考虑了滑动面的弹粘塑性变形，计算的安全系数的精度较高，但因未考虑岩块的变形，若岩块的尺度较大，计算的岩体位移可能有较大的误差，而对某些结构物（如拱坝坝肩），岩体位移的控制也很重要。

笔者从1994年开始试图发展一种广义弹粘塑性块体单元法以考虑岩块的变形（Chen，1994；陈胜宏，1996）。当时仅考虑了岩块的弹性变形，且用任意高阶多项式基函数分块拟合岩块的位移与应变分布。

一、基本理论模型

1.变形的几何方程

假定岩石块体单元rl的位移增量是一个多项式，即

其中

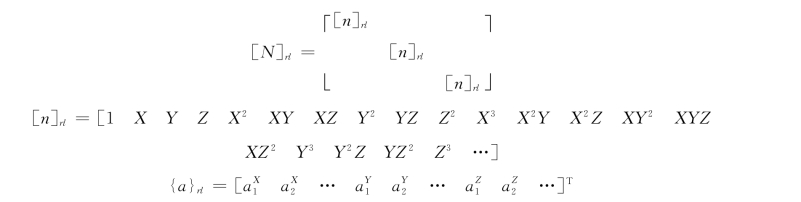
式中：[N]rl为位移函数；{a}rl为块体单元rl的参数向量。

第rl块体单元内的应变增量为

式中：[B]rl为应变矩阵。

若采用3阶逼近，则应变矩阵[B]rl可写为

结构面j rlrm上的相对位移增量为

式中：rl和rm是通过结构面j rlrm相邻的两个块体单元。

2.本构方程

根据块体单元为弹性的假定，第rl块体单元内的应力增量和应变增量的关系符合虎克定律，即

式中：[D]rl为弹性矩阵。

若采用显格式时步离散，在面jrlrm的任何积分点（x jrlrm，y jrlrm）上应力与变形的弹粘塑性本构关系为

弹性矩阵可由结构面的法向和切向刚度系数k n和k s表达，即

式中：γ为流动参数；Δt为时间步长；F jrlrm为屈服函数。

式中：φ、c和σT分别为结构面的摩擦角、凝聚力和抗拉强度。

3.平衡方程

块体单元系统的虚功方程可表达为

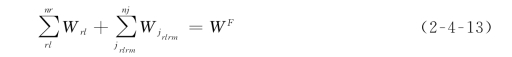
式中：W rl为块体单元rl的虚功；W jrlrm为结构面j rlrm的虚功；W F为外荷的虚功。

（1）块体单元rl的贡献。若块体单元rl产生虚位移{ΔU*}rl，对应的虚参数向量为{a*}rl，则有

块体单元rl的虚应变为

(www.xing528.com)

（3）外荷的虚功。由于结构面的厚度与块体单元尺度相比很小，故可忽略其内的体力，于是外荷的虚功为

块体单元荷载{Δf}rl的形式将在后面讨论。

4.由参数向量表达的平衡方程

组合所有块体单元后，块体单元系统的平衡方程可写为

其中，块体单元系统的刚度矩阵[K]为

块体单元系统的参数向量为

二、荷载移置

有两类荷载增量：①由结构面粘塑性变形产生的等效荷载增量{Δf vp}rl，其移置方式已在式（2-4-26）中给出；②外荷载增量{Δf}rl，下面按虚位移原理给出移置公式。

1.点荷载

3.面荷载

作用在块体单元rl的面j rlrm上，且密度为{Δp}=[Δp X Δp Y Δp Z]T的面力，其等效块体单元荷载为

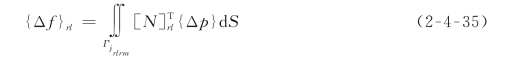
积分沿jrlrm面进行。

三、算例考察

对图2-4-3的重力坝剖面进行块体单元法分析，坝基含3条断层：F1、F2和F3，计算域含4个块体单元。采用图2-4-4所示网格进行有限单元法对比分析，计算参数如表2-4-4所示。

块体单元法分析中，把计算范围外的岩体视为一个全固定的整体，该整体与计算范围的岩体之间添加人工结构面，该结构面法向刚度极大而切向刚度极小（k n/ks＞106）。

地基的岩体初应力由下式计算

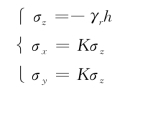
式中：h为埋深；γr为岩石容重，取γr=27k N/m3；K为侧压力系数，取K=0.3。

表2-4-4　计算参数

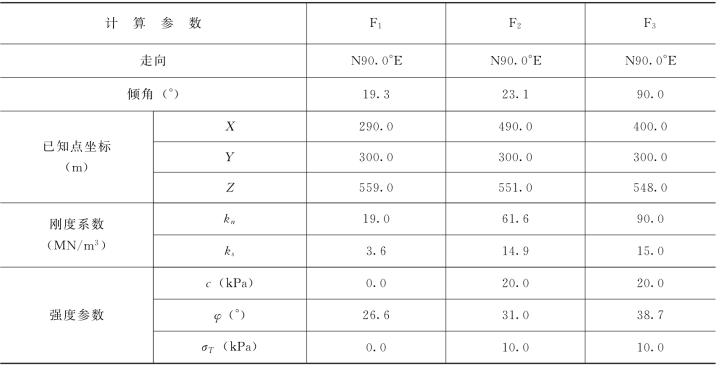
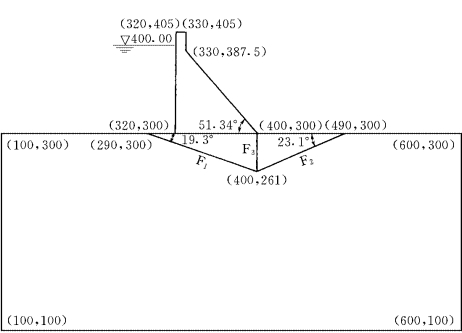
图2-4-3　重力坝剖面

岩石与混凝土的弹性模量和泊松比分别取为：Er=1500MPa，μr=0.2，E c=2000MPa，μc=0.15。混凝土的容重取γc=24k N/m3。

水库蓄水后的荷载有：

（1）上游坝面和库底面的静水压力。

（2）断层F1、F2和F3内的扬压力，按本篇第三章的方法计算。

块体单元法和有限单元法计算所得的位移和应力在分布规律方面一致，但在定量上两者尚有一定差距（陈胜宏，1996）。

图2-4-4　重力坝有限单元网格