数值分析与模型试验的比较对比

本节介绍两个楔形体的模型试验（Chen，1993）。通过试验与计算结果的比较，在某种程度上有助于了解块体单元法的适用条件和改进思路。

一、模型的设计

图2-4-1是楔形体试验模型的安装情况。共有两个不同的模型，楔形体的几何特性（参见图2-2-1）列于表2-4-1。

表2-4-1　楔形体的几何特性

图2-4-1　模型的安装

基础和楔形体用石膏制作，夹层用低强度的地质力学模型材料制作，其参数列于表2-4-2。

表2-4-2　夹层材料的力学参数

二、试验与计算结果(www.xing528.com)

在每一步荷载作用稳定后，记录楔形体外沿的铅直位移。当破坏发生时，位移快速增长，千斤顶的油压不能维持。

图2-4-2给出了在各荷载步下楔形体外沿铅直位移的试验与计算结果，位移曲线有以下两个显著特点：

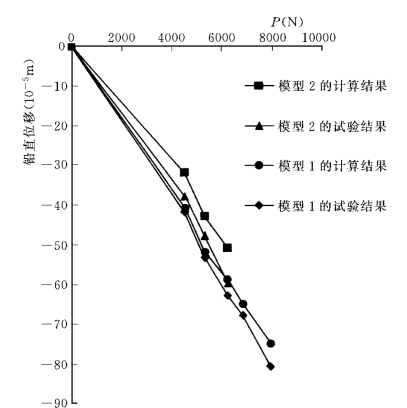
图2-4-2　楔形体外沿铅直位移

（1）模型1的位移大于模型2的位移。这是因为模型1的两滑动面夹角比模型2的小。

（2）模型1和模型2的位移实验值都比计算值大。这是因为常规弹粘塑性块体单元法未考虑块体单元的变形。

位移曲线有显著的位移增长拐点。模型1的试验拐点是P=6217～7348N，当压力超过7348N时楔形体失稳，而计算拐点是P=6782～7910N；模型2的试验和计算拐点都是P=5652～6217N。

试验和计算的极限荷载如表2-4-3所示。表2-4-3表明，当两滑动面夹角减小时，极限荷载增大，即安全系数增大，但刚体极限平衡法的安全系数增速过快；因弹粘塑性块体单元法考虑了滑动面的弹粘塑性变形，故计算的安全系数的精度较高。

表2-4-3　试验和计算的极限荷载