如何优化防渗帷幕的求解技术？

一、无压渗流分析

1.初流量法计算步骤

（1）求解方程式（2-3-20），得各结构面中结点水头{φ}e。

（2）在第r迭代步开始，利用等参单元插值求出各高斯点水头值。当φr＜Z时（Z为整体坐标系中垂直向上的坐标），说明该高斯点位于自由面之上；当φr＞Z时，说明该高斯点位于自由面之下。由此可以确定各结构面中自由面的近似位置。

（6）令r=r+1，重复步骤（2）～（5），直到计算结果满足精度要求为止。

2.计算精度控制标准

（1）φ＜Z的高斯点总数保持不变，即自由面位置基本稳定。

当上面两个控制标准同时满足时，计算结束。

3.自由面位置

各结构面中的自由面位置可以根据结点的水头函数关系，通过线性插值确定。

4.结构面上的逸出点位置

每次迭代计算之后，需对结构面上的逸出点位置进行判断和调整。根据结构面与逸出面交线上的各结点的水头值φ和坐标值Z的相对关系，可以确定出每次迭代后的逸出点位于哪两个结点之间，再近似以逸出点上的那个结点作为下一次迭代计算的逸出点。

待迭代计算结束后，对每个结构面的自由面进行拟合，求出其与逸出面的交点，即为所求的逸出点。

二、防渗帷幕和排水孔幕的模拟方法

防渗帷幕和排水孔幕对岩体渗流的影响很大。一套完整的岩体渗流分析方法与软件，必须包含有防渗帷幕和排水孔幕的模拟方法。(www.xing528.com)

1.防渗帷幕

在块体单元系统的渗流分析中已经假定岩石块体单元不透水，渗流只沿结构面进行。与此相对应，将防渗帷幕假定为一些由特殊结构面切割而成的特殊材料块体单元之后，也可假定防渗帷幕中的渗流只沿这些特殊块体单元的表面（即特殊结构面）进行。这些特殊结构面上的渗透系数取相对很小的值。

在这个基本假定下，防渗帷幕作为特殊块体单元而被纳入到整个块体单元系统中。在块体单元识别中，需指出所有的特殊块体单元（防渗帷幕）。在渗流分析中聚成整体导水矩阵时，将这些特殊块体单元表面的渗透系数取为相对小值。其他计算过程（如无压渗流分析等），与没有防渗帷幕时一样。

2.排水孔幕

由于排水孔数量多、孔径小，数值模拟有一定的难度。在有限单元法中较为成熟的有以沟代井法（关锦荷，刘嘉忻，朱玉侠，1984；毛昶熙，李祖贻，陈平，1989）、排水子结构法（王镭，刘中，张有天，1992；朱岳明，陈振雷，陈晴，徐爱忠，1996）和半解析法（詹美礼，速宝玉，刘俊勇，2000）。笔者在块体单元法中，将排水孔幕按等效结构面处理（汪卫明，徐明毅，陈胜宏，2001）。根据排水孔幕布置的主倾向和主倾角，将排水孔幕等效为一个平面结构面或几个折平面结构面，等效结构面的渗透系数可由排水孔半径、排水孔间距以及岩石的渗透系数推算。

三、边界预调整法

因无压渗流场的自由面边界和逸出面边界条件都是未知的，需要进行迭代求解。当边界条件相对比较简单、待求解渗流场的梯度变化相对比较平缓时，直接以有压渗流计算的渗流场为初值，经过若干次迭代后能够收敛。但是当边界条件比较复杂，渗流场的梯度变化比较大时，仍然按前述方法进行迭代求解则有可能会导致收敛速度慢甚至不收敛。

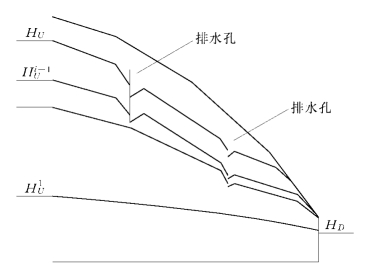
图2-3-1　边界预调整过程示意图

如果将自由面边界和逸出面边界抽象成两个变量，将整个无压渗流问题抽象成一个二元非线性方程组，那么按上述迭代过程求解无压渗流场的方法属于解非线性方程组的简单迭代法，其收敛条件是方程组满足非局部收敛定理。显然，随着方程组非线性程度的增加，按有压渗流计算的渗流场初值与精确解相差会越来越大，采用简单迭代法可能会导致计算过程不收敛。解决这类问题的一个途径就是选择一个比较接近精确解的渗流场初值，在此基础上进行无压渗流迭代计算。这样，只需方程组局部收敛，即可保证迭代过程收敛于精确解。

基于上面的考虑，笔者提出一种比较实用的边界预调整法（汪卫明，徐明毅，陈胜宏，2001），以适应复杂边界条件下无压渗流分析的需要。其基本思想是将上游水位和天然地下水位分成若干级进行分步计算，根据本步计算的渗流场，对下一步计算的逸出面边界条件进行预调整（图2-3-1）。具体计算步骤如下：

（1）将上游水位H U和天然地下水位H G分成n级，第i级水位为

（5）进行无压渗流迭代计算。按式（2-3-23）计算第r次迭代后位于自由面以上区域的高斯点对单元结点初流量的贡献，并叠加到方程的右端项中，得到第r+1次迭代的方程式（2-3-24）。当达到精度要求时，迭代计算结束。

所谓的边界预调整，实际上是通过迭代进行的一种比较粗略的边界求解过程，边界的细微调整仍然是在步骤（5）的无压渗流迭代计算中，伴随着内部渗流场的求解来进行的。通过边界预调整，可以大体上将边界和内部渗流场解耦，使最后的初流量法迭代过程在比较准确的边界条件下进行，从而避免自由面边界的大幅波动和迭代过程的不收敛。

边界预调整中的水位分级是根据渗流场的边界条件、防排设施的布置和渗流场梯度变化的剧烈程度等来确定的。对于复杂的渗流问题，一般取n=8～15就可以满足要求。