在计算岩体力学中,经常会遇到这样的情况:考虑范围内的岩体被许多大尺度断层或夹层等结构面切割成块体单元系统,稳定和变形的主要控制因素为结构面。
对岩坡中楔形体的研究表明:滑动面上应力状态的主要影响因素除强度参数外,还有滑动面的几何特性与变形特性,而楔形体和围岩的变形及强度参数的影响则很小;若把楔形体和围岩作为刚体,仅考虑滑动面的变形及强度特性,通过建立楔形体的整体平衡方程、滑动面变形与楔形体位移的几何相容方程、滑动面变形与应力的弹粘塑性本构方程,即可建立求解楔形体变形与稳定的基本方程。
笔者把这个思路推广到复杂的三维块体单元系统,建立了不连续岩体的弹粘塑性块体单元理论和相应的块体单元分析方法(陈胜宏,王鸿儒,熊文林,1988;陈胜宏,1991),该法假定块体单元之间为面—面接触,主要是因为:
(1)坝基或坝肩岩体作为结构物,在正常工作极限状态一般不允许出现点—面接触变形或点—点接触变形。
(2)工程设计提供的结构面变形和强度参数也都是在面—面接触假定下获取的。
常规的弹粘塑性块体单元法还假定岩石块体单元为刚体,仅考虑结构面的变形和强度特性。在这些基本假定的基础上,通过建立块体单元系统的整体平衡方程、结构面的变形与块体单元位移的几何相容方程,以及结构面的弹粘塑性本构方程,即可推导出求解块体单元系统位移与稳定的基本方程。
一、坐标系和数学符号的约定
以rl为代表块体单元,块体单元的边界面记为jrlrm,并把通过面j rlrm与块体单元rl接触的块体单元记为rm(图2-2-4)。
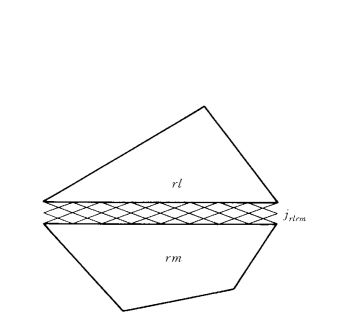
图2-2-4 块体单元rl和块体单元rm的接触关系

图2-2-5 坐标系
建立如图2-2-5所示的整体坐标系:X轴水平向东,Y轴水平向北,Z轴铅直向上,整体坐标用(X,Y,Z)表示。
在图2-2-5所示坐标系下,第j rlrm个结构面的平面方程可写为

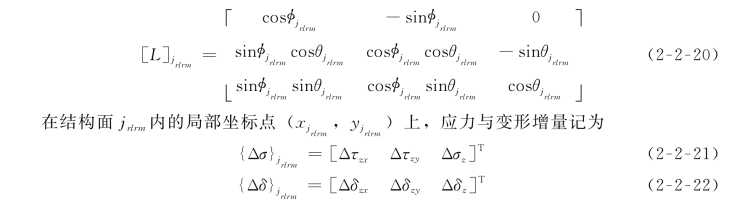
作用于块体单元rl的荷载增量向其形心简化,结果将是3个力矢增量与3个力矩增量,在整体坐标系中记为
![]()
对应的块体单元位移增量在整体坐标系中为
![]()
二、基本方程
1.块体单元的力与力矩平衡方程
对块体单元rl各面上的应力进行积分,并向块体单元的形心简化(图2-2-6),可在整体坐标系统中写出块体单元的平衡方程为

式中:{X 0}jrlrm为面j rlrm形心的整体坐标;{X 0}rl为块体单元rl形心的整体坐标。
2.块体单元形心位移与结构面变形的几何相容方程
岩石块体单元rl和rm的位移增量将在结构面j rlrm两侧岩体上引起相对变位(或变形){Δδ}jrlrm,应用运动学原理可推出两者关系为
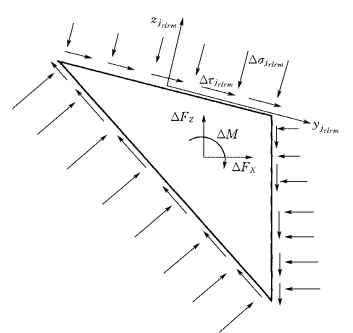
图2-2-6 块体单元的平衡

图2-2-7 块体单元变形协调关系
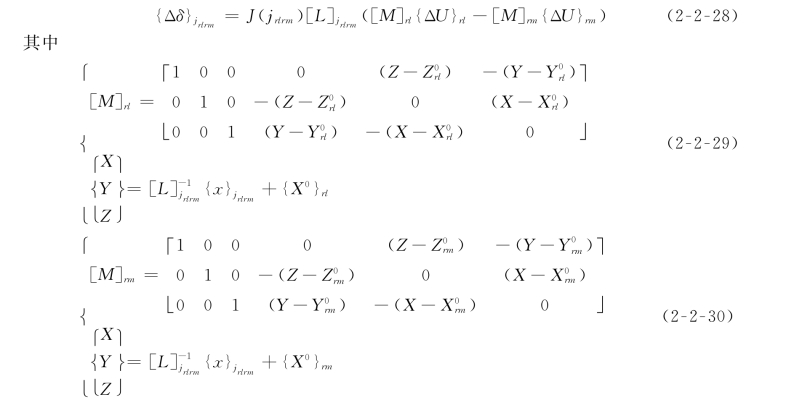
3.结构面的弹粘塑性本构方程
根据一般弹粘塑性势理论(Owen,Hinton,1980),若采用显格式时步离散,在面j rlrm的任何积分点(x jrlrm,y jrlrm)上应力与变形的关系为
![]()
弹性矩阵可由结构面的法向和切向刚度系数kn和k s表达,即


式中:φ、c和σT分别为结构面的摩擦角、凝聚力和抗拉强度。
4.块体单元系统的整体平衡方程
将式(2-2-28)和式(2-2-31)代入式(2-2-23),块体单元rl的平衡方程为
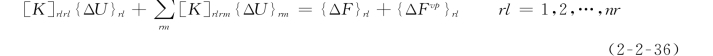
式(2-2-36)中,rm走遍(与面jrlrm对应)rl的所有邻块,且
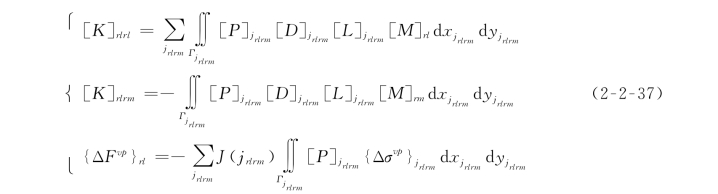
其他所有可动块体单元都存在以上形式的方程,经组合即构成块体单元系统的整体平衡方程,即

式中:{ΔF}、{ΔFvp}和{ΔU}分别为块体单元系统的外荷载增量、等效粘塑性荷载增量和位移增量。
在任一时间步,首先由式(2-2-38)解出块体单元形心位移增量{ΔU},然后由式(2-2-28)计算结构面j rlrm上的变形增量{Δδ}jrlrm,接着由式(2-2-31)计算结构面j rlrm的应力增量{Δσ}jrlrm,从式(2-2-33)、式(2-2-34)和式(2-2-37)求出粘塑性应力增量{Δσvp}jrlrm和等效荷载增量{ΔF vp}rl后,即转入下一时步的计算。若某些结构面的强度降到一定值,使得以上计算发散,则说明某些块体单元或块体单元组合已不能维持平衡,据此即得出该块体单元或块体单元组合的安全系数。
三、块体单元系统的积分法
计算式(2-2-37)中的[K]rlrl、[K]rlrm和[ΔF vp]rl,需在结构面上进行积分。在某些情况下,甚至还要在块体单元内部积分。因块体单元及其由结构面形成的界面形状各异,故很难给出显式的积分结果。笔者提出一种结构面上和块体单元内部的高斯积分法。
1.结构面的积分法
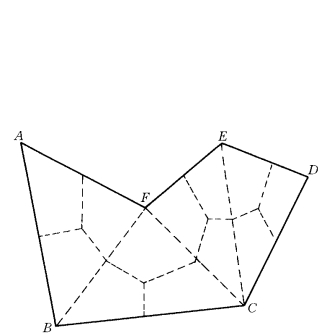
图2-2-8是某一块体单元的一个面,其顶点数是n v。先采用简单的方法将其离散成(nv-2)个三角形。然后对每个三角形,从其形心到各边中点作直线,即可将其分为3个四边形。
利用等参单元法中的形函数变换,式(2-2-37)可转化为
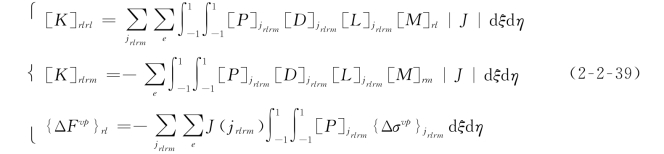
式中:e为j rlrm面所分的四边形数目;|J|为雅可比行列式。
通常,取两点高斯积分格式即可有足够的精度。
 (https://www.xing528.com)
(https://www.xing528.com)
图2-2-8 结构面的积分单元划分
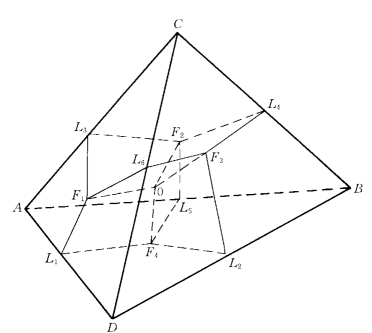
图2-2-9 块体单元的积分单元划分
2.块体单元内部的积分法
首先把块体单元分成若干个四面体,然后对每个四面体进行如图2-2-9所示的划分:从该四面体形心到各面形心作直线,并从各面形心到各边中心作直线,即可将其分为若干个六面体。
利用等参单元法中的形函数变换,任何定义于块体单元内的函数F(X,Y,Z)积分均可转化为
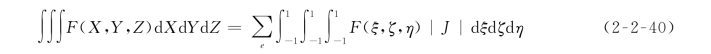
式中:e为块体单元rl所分的六面体数。
四、岩石块体单元组合的安全系数
采用弹粘塑性块体单元法计算岩体的整体稳定强度储备安全系数比较简单,只要把所有结构面的强度指标按一定规律调整试算即可。但工程界经常关心某些特定的块体单元组合的安全系数,此时需要对这些特定的块体单元组合逐一计算其安全系数。问题是,有时并不知道哪些块体单元组合是危险的和重要的。笔者建议先按常规的刚体极限平衡法进行分析,从大量的块体单元组合中寻找安全系数较小的一些特定块体单元组合。这些极限平衡法的分析成果是常规设计所必须的,也可作为弹粘塑性块体单元法进一步分析的依据,而且两者可以相互验证。
刚体极限平衡法受到广大工程技术人员的喜爱,并具有丰富的工程实践经验。石根华在1977年提出关键块理论,该理论能计算出岩体中最先滑动的块体,若能把这些关键块体锚固住,岩体就能保持稳定。1988年,林德彰又提出另外一种块体分析的方法,其特点是:在确定被节理切割的块体的几何参数时,采用了代数拓扑学中同调论的方法。关键块理论只分析了块体沿一个或两个面的滑动而略去了倾倒,林氏分析中,不但分析了块体的滑动,也分析了块体的倾倒旋转。在某些时候,发生滑动破坏的不是某些单个的块体,而是一些块体的组合。如何搜索不规则块体系统中最危险的滑动组合,迄今为止还未见有很好的方法被报道过。笔者在刚体极限平衡法的基础上,建立了采用树状结构深度优先的启发式搜索方法,寻找岩体中从最危险到较危险的一系列滑动组合,计算出相应的安全系数(徐明毅,汪卫明,陈胜宏,2000)。
(一)块体单元组合可动性和破坏模式的判别
石根华把块体的基本类型分为:

块体理论的基本方法是首先通过几何分析,排除所有的无限块体和不可动块体;然后通过运动学分析,找出在工程作用力和自重作用下的所有可能失稳的块体;再根据滑动面的物理力学性质,确定开挖面上所有的关键块体。无限块体、不可动块体及稳定块体都可以归为一类,即安全系数可认为无限大;而可能失稳块体和关键块体可归为一类,其中关键块体由于安全系数最小,若不满足安全要求,则必须加以锚固才能保持稳定。
在实际工程中,最容易滑动的不一定是节理面切出的单个块体,而可能是一些块体的组合体。如果在单个块体中找到一个最小的稳定安全系数作为岩体的安全系数,结果可能是偏于不安全的。应该考虑单个块体以及块体组合中最危险的情况,搜索出的最小安全系数才能代表岩体的整体安全系数。以二维问题为例(图2-2-10),按照单个块体判断,A最容易失稳,是关键块体。而实际上最危险的是块体组合A+B,如果以A为关键块体进行加固设计,则锚固力不足,按块体组合A+B进行加固设计,才能保证安全。空间块体具有同样的情况。
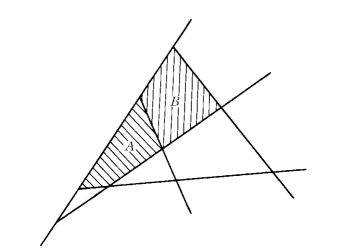
图2-2-10 二维块体组合
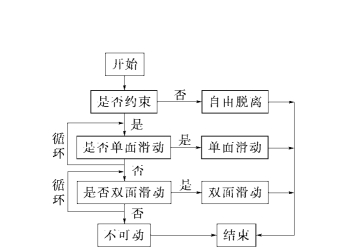
图2-2-11 块体组合的判断过程
块体理论中的刚体极限平衡分析采用如下假设:滑移体为刚体,滑移面为平面,滑面上的应力均匀分布,有抗剪的凝聚力和一定的摩擦系数,只能抗压不能抗拉,极限状态下只考虑共点力的平衡,不考虑力矩的平衡。
块体有3种滑动破坏方式:
(1)无滑动面的自由脱落。
(2)单面滑动。
(3)双面滑动。
自由脱落的安全系数为0,单面滑动安全系数的计算简单,双面滑动安全系数的计算常用矢量代数方法,其实质已在本章第一节进行了介绍。对某一组合,计算的程序框图如图2-2-11所示。
(二)危险滑动组合体的搜索方法
1.提高搜索效率的方法

(1)修改搜索空间,使搜索过程更容易。可以在搜索过程开始前就修改搜索空间,也可以在搜索过程中修改搜索空间,一般能在很大程度上缩减问题的规模。
(2)提出一些在大多数情况下能有助于求解的通用的启发信息,对最可能成为解的情况进行优先搜索。
(3)用特定的结构调整搜索过程。
针对边坡稳定问题,可以采用以下方法减少搜索次数,并尽快地搜索到最危险的块体单元组合。首先,排除一些不可能滑动的块体单元,缩小搜索空间。仿照林德彰的做法:在初始自由面时,有关键块脱落或者滑动,则去掉这些块体单元;出现新的临空面,与之相邻的一些块体单元随即发生失稳,因此把它们去掉;再计算下一轮不稳定的块体单元。最后剩下不可动的块体单元,它们不会参与任何滑动,因此可以把它们从搜索范围内去掉。这样就在很大程度上为组合搜索减轻了压力。如果要进一步减小搜索范围,可以通过人工判断,指定搜索可能滑动区域内的块体单元。
确定搜索范围后,就要选定具体的搜索方法。采用任意组合的方式浪费很大,如果从一个块体单元开始,根据相邻关系逐步扩大组合块体单元,每一次搜索就是一个真实存在的块体单元组合,组合数就能减少很多。这种根据空间拓扑信息来大量减少搜索量的方法也是一种启发式信息的利用。
另外,为了尽快搜索到最危险的块体单元组合,在选定相邻的块体单元进行组合时,按这些块体单元的稳定安全系数进行排序,稳定安全系数小的优先组合,就可以用尽可能少的次数搜索到最危险的组合块体单元。
根据以上讨论,搜索过程按以下思路组织:在初始自由面时,计算有可能失稳的关键块体单元,并按安全系数排序,选定最小的一个作为第一个种子点,从该块体单元开始进行组合。把该块体单元脱离出来,与之相邻的块体单元由于新的临空面出现而可能滑动,按安全系数大小排序,确定该层的待组合块体单元。先选择该层安全系数最小的块体单元组合到脱离块体单元上,计算此组合块体单元的抗滑稳定安全系数,如果比原来小,则把该组合记录下来。同理,小块体单元组合到脱离块体单元上之后,又出现新的临空面,按同样的方法进行判断,选择相邻的最容易滑动的块体单元进行组合,并计算组合块体单元的安全系数,同先前的组合进行比较,以决定是否保留。达到一定的层次后,与之相邻的块体单元或者没有,或者是排除在搜索范围外的块体单元,也就是没有块体单元可供组合了,这时,就把该层选定的块体单元返回到原块体单元系统,用该层的下一个待组合块体单元进行组合,如果该层已组合完毕,则需要返回到上一层,也就是进行回溯。这样,通过在组合块体单元上不断地增加或减少块体单元,就能对组合空间进行有序的搜索。整个搜索过程是一种深度优先带回溯的启发式搜索,如图2-2-12所示。
由于搜索层次在动态变化,需要有较好的数据结构来进行管理。要记录搜索层次的变化,对每一层用指针记录下用来组合的块体单元,这样在搜索到较小的抗滑稳定安全系数时,才能把该块体单元组合记录下来。
搜索中主要的操作是对某层的待组合块体单元按安全系数大小排序,把选定的块体单元组合到脱离块体单元上,以及把不需要的块体单元返回到原块体单元系统。增加块体单元和返回块体单元相应的处理是:
(1)将小块体单元增加到组合体。
1)粘附在原块体单元系统的标识变为0。

图2-2-12 搜索的树状结构
2)组合块体单元的变化。删去小块体单元和组合块体单元共同的面;加上属于小块体单元的面而不属于原组合块体单元的面;组合块体单元的体力加上小块体单元的体力。
3)原块体单元系统的变化。与小块体单元相邻的块体单元的非临空面因去掉小块体单元而变成临空面。
(2)小块体单元返回到原块体单元系统。
1)粘附在原块体单元系统的标识变为1。
2)组合体的变化。删去属于小块体单元的面而不属于原组合块体单元的面;属于小块体单元和原组合块体单元的相邻面因被删去而要补上;组合块体单元的体力减去小块体单元的体力。
3)原块体单元系统的变化。与小块体单元相邻的块体单元的临空面因补加小块体单元而变成非临空面。
2.搜索的步骤
(1)在初始自由面时,计算可能失稳块体单元,并按安全系数排序,安全系数小的排在前面,作为第1层待组合块体单元,层数N=1,该层指针IP 1=1。
(2)将IP 1对应的块体单元作为种子点,从该块体单元开始进行组合。
(3)组合块体单元脱离出来,与之相邻的块体单元由于新的临空面出现而可能滑动,按安全系数大小排序,确定下一层的待组合块体单元。如果待组合块体单元非空,令N=N+1,指针IP N=1,到步骤(4)。如果待组合块体单元为空,转到步骤(6)。
(4)将IP N对应的块体单元增加到组合块体单元上。删去组合块体单元和小块体单元共同的面,增加属于小块体单元而不属于原组合块体单元的面,同时组合块体单元的体力加上小块体单元的体力。原块体单元系统中与小块体单元相邻的面因去掉小块体单元而变成临空面。
(5)计算组合块体单元的抗滑稳定安全系数,如果安全系数较小,则把该组合记录下来,使各层指针IP 1~IP N指向对应的块体单元号,并转到步骤(3)。
(6)将IP N对应的块体单元返回到原块体单元系统。这与步骤(4)的操作正好相反。
(7)IP N=IP N+1,如果在该层范围内,则转到步骤(4)。否则,转到步骤(8)。
(8)缩减层次,N=N-1,若N>1,则转向步骤(6);若N=1,则转向步骤(2);若N=0,则搜索完毕。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




