如何计算不规则曲面模拟中的多边形面矢？

1.不规则地形面的模拟

工程中的地形面都是不规则曲面，而可能获得的基础数据却只有一些离散点的坐标。通常给出的点都是很具有代表性的点，基本上能反映出地形的不规则性。有关类似于地形面的不规则曲面模拟的理论与方法已在第一篇第二章第二节中进行了讨论。笔者在块体单元识别软件中采用下式来模拟地形面

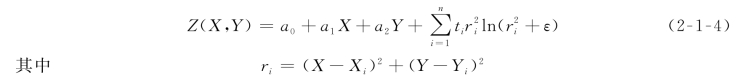
式中：a 0、a 1、a 2、ti为常数；ε为一个很小的正数，一般取ε=0.001。

将离散点的坐标（X i，Y i，Zi）（i=1，2，…，n）代入式（2-1-4），可得到n个线性方程。但是该式中共有n+3个待定系数，因此需要补充以下强迫条件

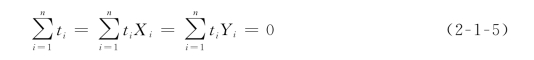
式（2-1-4）应用起来比较简单，从后面的算例也可以看出，所模拟出的曲面与实际地形面拟合较好。

2.求两个平面与地形面的交点

两个平面的数学表达式可以写为

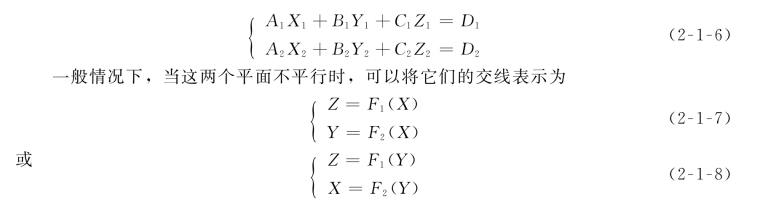
以式（2-1-7）为例说明交点的算法。首先将交线沿X方向离散成有限个线段，离散步长ΔX需根据地形面的起伏度来确定。对每条线段的两个端点（X i，Y i，Zi）和（X j，Y j，Zj），由地形面插值公式求出Z（X i，Y i）和Z（X j，Y j），即可按下面的方法来判断它们是否与地形面相交。如果[Z（X i，Y i）-Zi][Z（X j，Y j）-Z j]＜0，则该线段与地形面相交，采用二分法即可求得交点；否则，该线段与地形面不相交。

3.对曲线上的点排序

当一个平面与地形面相交时，交线是一条曲线。对直线上的点只需按照直线的方向排序，就可以找到所有的边。对曲线上的点排序，却复杂得多，可以采用沿曲线逐步迭代找点的方法对曲线上的点排序，从而生成曲边。

一般情况下，一个平面（方程为AX+BY+CZ=D）与地形面相交形成的交线投影到水平面上可以写成下面的形式

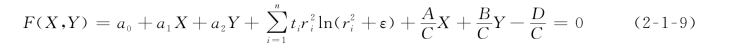
式（2-1-9）是一个非线性方程。若已知X（或Y），要求解Y（或X），一般可以采用迭代的方法。因此，将式（2-1-9）写成迭代形式，即

从曲线上某一已知顶点（X 0，Y 0）开始，将X坐标值（或Y坐标值）按照合适的步长离散，然后采用Newton迭代法，逐步求出Y坐标值（或X坐标值）。若某一迭代过程不收敛，则改变其步长，直到收敛而且结果满足精度要求。当计算过程中遇到另外一个已知顶点时，这两个点所夹的曲线就形成一条曲边（图2-1-12）。这样便可以依次识别出曲线上的所有曲边。

曲边生成过程中计算出来的各中间点坐标值，将用来对曲面进行离散，以及曲面面积的计算、含曲矢面的矢体体积计算和地形面等值线的绘制。

4.判断一点是否在多边形内

在矢面的生成、三维图形的消隐和曲面的离散等很多算法中，都需要用到判断一点是否在多边形内的算法。采用求各边对该点所张的夹角和的方法可以解决这个问题。(www.xing528.com)

图2-1-12　沿曲线的变步长迭代排序方法

图2-1-13　判断一点是否在多边形矢面内

5.计算矢面的面矢

由于矢面往往是不规则多边形，不能直接计算它的面积。但如果将其转化成三角形面积计算，则可以很简单地计算出它的面积，从而确定它的面矢。

对于平面多边形矢面，可以通过平面上的任意一点P将其化为若干个三角形矢面。分别计算出每个三角形矢面的面矢，它们的和即为所求多边形矢面的面矢。其数学表达式为

对于曲矢面，虽然它的各矢边不在同一个平面上，但是由于式（2-1-12）中计算面积所用的基本形是三角形，不存在扭曲的问题，因此仍然可以利用式（2-1-12）来计算它的面矢。

6.计算矢体的体积

与前面介绍的矢面面积计算方法类似，必须将复杂形状矢体的体积计算转化成简单形状矢体的体积计算。计算体积时可用棱锥体作为基本形。

对于包含有曲矢面的矢体，用式（2-1-15）计算出的体积只是精度很低的近似值。高精度的体积计算必须将曲面离散成很多三角形之后，再利用式（2-1-15）计算。

7.地形面等值线的计算

采用等值线描述地形面比较方便，而且是符合工程习惯的一种方法。

由于有了曲面的三角形面离散作为基础，因此可以运用线性插值全域扫描法计算等值线。假定所有三角形面内的Z坐标值呈线性变化，在计算Z=Z 0的等值线时，对每个三角形的三条边计算下式的值

显然，当Z=Z 0的等值线穿过三角形的一条边时，必然穿过它的另一条边。

用线性插值全域扫描法计算出的等值线是由直线段连接而成的，需要时可以对这些等值线进行光滑化（用曲线拟合）。一般情况下，当离散的三角形比较小时，计算出的等值线的视觉效果也相当好。