应变局部化：材料软化阶段下的结构破坏现象

一般来说，分叉和应变局部化与材料的软化特性密切相关。在弹塑性分析中，当材料进入软化阶段后，通常会发生分叉和应变局部化等现象（Ottosen，1991；Neilsen，Schreyer，1993；陆启韵，1995）。当材料为非关联弹塑性时，这些现象在强化阶段就会出现。应变局部化是结构破坏过程中的重要现象，其数值模拟是国际上的研究热点（钱伟长，1988；白以龙，1995；陆明万，罗学富，郑长卿，1995；曾亚武，陶振宇，赵震英，1999；沈珠江，2000）。

一、材料的分叉和解的唯一性

常规有限单元法在处理应变局部化问题时往往失效，主要表现为有限单元法的解丧失唯一性，计算结果病态地依赖计算网格。

按有限单元法的常规表示，一个离散体系由荷载增量{ΔF}引起的结点位移增量{Δδ}应满足下列方程

对于一个稳定问题，解{Δδ}应该存在并且唯一。但是在一定条件下，可能出现解的不定和分叉。假定在基本解{Δδ}之外，还存在一个分叉解{Δδ1}，均满足式（1-13-2），则两式相减得

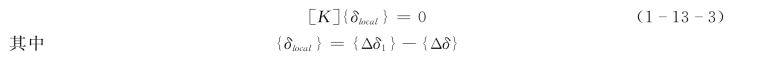
显然，式（1-13-3）有非零解的条件是

式（1-13-4）也是出现分叉解的必要条件。

关于这个问题可以从有限单元法的数学理论作进一步的讨论。建立有限单元法方程的微分方程边值问题的变分提法为：

V是Hilbert空间，B（u，v）是V*V上的双线性泛函，F（v）是V上的有界连续泛函。

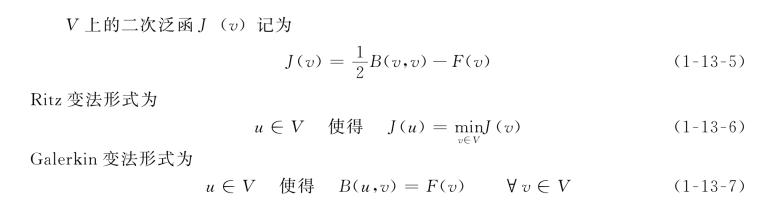
一个基本正确描述所考虑物理模型的微分方程定解问题，其解通常是存在、唯一并且是稳定的。关于这个问题的深入讨论属于微分方程广义解的适定性研究领域，这里仅给出几个基本定理。

定理1 V是Hilbert空间，B（u，v）是V*V上的双线性泛函，满足

（1）对称性

（2）正定性（强制性）

（3）有界性（连续性）

M、γ是不依赖于u、v的正常数，‖·‖是V中的范数，则

（1）变分问题的两种提法是等价的，即其中任何一个问题的解必是另一个问题的解。(www.xing528.com)

（2）如果变分问题有解，则解是唯一的。

定理2（Lax-Milgram定理）V是Hilbert空间，其内积和范数分别是（·，·）和‖·‖，B（u，v）是V*V上的双线性泛函，且满足定理1中的对称性、正定性、有界性条件，F（v）是V上的有界连续泛函，则存在唯一的u*∈V，使得

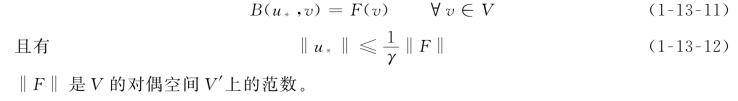
若去掉关于B（u，v）的对称条件，结论仍然成立，但此时变分问题的两种提法不再等价。

在力学中，由二阶椭圆边值问题的上述两类变分提法可分别得出极小位能原理和虚功原理，从而建立有限单元方程。其中极小位能原理只适用于保守力场、弹性材料等对称正定的边值问题，此时有限单元刚度矩阵为对称正定矩阵。虚功原理对此没有要求，即使材料进入软化区域，仍可根据虚功原理建立有限单元平衡方程，但解不唯一且不稳定。下面通过分析材料软化阶段刚度矩阵的特性来说明这个问题。

记K、G、P、Q分别为压缩模量、剪切模量、压硬模量和剪缩模量，Δσm、Δτ、Δεv、Δγ分别为静水压力增量、广义剪应力增量、体积应变增量和广义剪应变增量，则有

式（1-13-17）右边前3项只含应变分量的平方项，因此在弹性条件（不考虑压硬和剪缩）下，ΔW恒为正，即刚度矩阵正定性得到保证。如果P=Q，第4项为0，则可以得到同样的结论；反之，当P≠Q，甚至P＜0，Q＞0，即压硬剪胀材料（这在岩体中是很常见的），在应变分量Δεx、Δεy和Δγ的一定组合下，ΔW可能小于0，刚度矩阵失去正定性，解不唯一且不稳定。

上述问题在数值上的反映为当软化区和硬化区同时存在时，对应于两区交界面所形成的矩阵的主对角元素可能为负或为0，或者矩阵分解过程中主对角元素为负或为0，从而导致计算无法进行或出现很大的误差。

二、解对于网格的依赖性（Needleman，1988）

由于方程椭圆性丧失，局部化区域的形状、宽度随网格的大小改变而变化（Larsson，Runesson，1991），并且当有限单元网格加密时，在应变局部化区域的能量逸散错误地趋向零，有限单元计算收敛到不正确的、没有物理意义的一种结果。关于这个问题可以参见下面的一个一维算例（De Borst，1987）。

三、研究现状简评

图1-13-9　受拉杆（划分为m个单元）

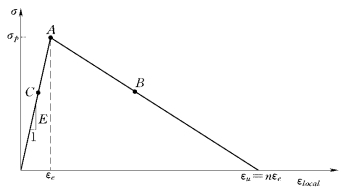
图1-13-10　材料的应力—应变关系（弹性—软化）

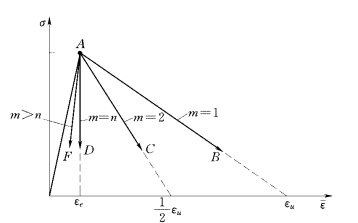
图1-13-11　不同单元划分下杆的平均应变

近十几年来，许多学者从不同的角度对局部化问题进行了研究。根据对许多工程材料的实验观察，一些学者认为，在发生应变局部化之前，材料微观裂隙和微观空洞的生成与发展过程是近似均匀的，经典连续介质力学能够很好地模拟这个过程，而对于高度局部化的宏观裂缝等现象，经典连续介质力学则不再适用。在这种理解下，广义连续体理论被引入。在广义连续体理论中，作为正则化机制引入了内部长度参数和高阶连续结构，以保持方程的椭圆性。主要的广义连续体理论有非局部应变理论、梯度塑性理论（De Borst，Muhlhaus，1992；宋二祥，1995；李锡夔，Cescott，1996；）、Cosserat连续体理论（Muhlhaus，1989）。还有一些学者在经典连续介质理论的框架内进行讨论，主要的方法有：应变局部化分叉分析（De Borst，1988）、特殊形函数法（Ortiz，Leroy，Needleman，1987）、复合体方法（Pietruszczak，Mroz，1981；Pietruszczak，Niu，1993）和自适应有限单元法（Deb，Prevost，Loret，1996；黄茂松，钱建固，吴世明，2001）。

h型自适应有限单元法能够随着变形的发展不断调整网格的形状和大小，所以与其他方法比较，在处理应变局部化问题时有着特别的优势。由于控制方程椭圆性的丧失，以前应用于h型自适应有限单元法的行之有效的误差分析方法已不再适用，也不再有一个全局性的误差准则，取而代之的是一些单元水平上的准则，如位移在单元内的变化、等效应变能等。这些准则如同分叉分析一样均是局部化的，因此运用这些准则的h型有限单元法可称为局部化自适应有限单元法。若某单元满足上述准则，即认为该单元进入局部化，并按照某种方法将该单元（母单元）细分为若干个子单元，Ortiz等人（Ortiz，Quigley，1991）、Deb等人（Deb，Prevost，Loret，1996）、Belytschko等人（Belytschko，Tabbara，1993）运用不同的方法实现这种细分。由于这些误差分析准则不能给出网格优化的量化指标（如大小、方向等），故这种细分并不能保证网格的充分优化，而且在三维条件下单元的细分往往是困难的。与局部化自适应有限单元法相对应，Zienkiewicz等人（Zienkiewicz，Huang，1995）运用全局网格优化来解决应变局部化问题，这种方法与常规h型自适应有限单元法更加相似：用行波法在整个计算域内全部重画网格，单元的伸长方向与局部带方向一致。这种方法克服了局部化自适应有限单元法的缺点，且适合在三维条件下运用。但批评者认为该法没有充分考虑应变局部化的力学特征，因而不能及时准确地捕捉局部化带。

笔者认为，应变局部化问题是一个难度较大的研究课题，虽然已经取得了一些进展，但还有许多问题有待解决。这方面的研究动态值得关注。