岩石边坡的稳定安全系数分析方法及其评价

对各类工程结构，用有限单元法分析可以获得位移、应力、稳定安全系数等指标。这些指标的控制标准取值是非常重要的问题。本节以岩石边坡稳定安全系数为例进行讨论。

目前对岩石边坡进行稳定分析的方法很多。在定量分析方法领域，最初发展起来的刚体极限平衡法凭借其简便和实用的优势，仍然占有重要的地位；有限单元法在计算手段日益改进的促进下，也得到了迅速的发展；近年来又陆续出现了一批针对岩体不连续性的分析方法。这些方法各具特色，基本假定和考虑因素不尽相同。如何评价这些方法的有效性及合理性，确定它们在具有同等安全程度条件下的安全系数取值标准，是从理论和方法研究到工程应用过渡的关键。

一、安全系数的表达

比较常用的岩石边坡稳定安全系数的定义有3种：

（1）应力总和安全系数。Wright等人（Wright，Ulhawwy，Duncan，1973）和Yamagami等人（Yamagami，Ueta，1988）在边坡中定义一个潜在的滑裂面，完成应力应变分析后，滑裂面的整体安全系数K定义为抗滑力和滑动力的比值，即

式中：σi、τi、f i、ci分别为滑裂面上第i个单元的法向正应力、剪应力、摩擦系数和凝聚力；l i为该单元沿滑裂面的长度。

（2）超载安全系数。将荷载乘以K，并将K逐渐增大或减小。对于每一个K值都进行一次分析，直到K值达到某个临界值，使得边坡失稳为止。这个临界K值就是超载安全系数，即如果荷载增大到原来的K倍，边坡即处于失稳状态。

（3）强度储备安全系数。将岩体的强度除以K，并将K逐渐增大或减小。对于每一个K值都进行一次分析，直到K值达到某个临界值，使得边坡失稳为止。这个临界K值就是强度储备安全系数，即如果岩体的强度降低到原来的K倍，边坡即处于失稳状态。国内外不少学者（Griffith，Lane，1999；赵尚毅，郑颖人，时卫民，王敬林，2002；任青文，钱向东，2002）在这方面作了有益的探索，并取得了一些成果。笔者在AFEAS分析软件中也实现了强度储备安全系数的计算功能。

在水利水电工程中，目前多趋向于采用强度储备安全系数，其根据是：

（1）边坡上作用的外荷载较为明确，而岩体强度的变化较大且不易精确确定。

（2）边坡中岩体自重往往是最主要的荷载，但自重既产生下滑力，也产生阻滑力，采用超载系数的概念不明确。

（3）应力总和安全系数在力学上不够严谨。

二、稳定性判据

在推求边坡的强度储备安全系数的过程中，需要一个判断标准：什么时候边坡达到极限状态？

边坡失稳的实质是强度破坏。当滑动面的应力达到强度极限时，边坡处于极限平衡状态，此时只要有一个小的扰动，边坡就将偏离原平衡状态而不能恢复，即由静止状态向可动状态转变。这种失稳现象由于其应力—变形曲线具有极值点，属于极值点失稳类型，理论上可以采用以下失稳判据：

（1）收敛性判据。在求解迭代中，当系统的位移增量曲线或者荷载增量曲线达到极值点后，在计算上即反应出迭代过程不收敛。因此若在弹粘塑性分析过程中，排除其他原因之后，发现迭代计算不收敛，即可以作为系统失稳的判据。

（2）能量判据。根据功能原理，系统的内能和外力对系统所做的外功应相等。当强度折减到一定程度后，若外功大于内能，则可以认为系统已经破坏，并以此作为系统失稳的判据（卓家寿，1997）。

（3）突变性判据。突变性判据认为任何能够反映系统状态突变的现象（如位移突然变大、高斯点大面积屈服和屈服区连通等）都可以作为失稳的判据。

（4）极限平衡判据。在强度折减的过程中，搜索使式（1-13-1）表达的安全系数达到最小的滑裂面，当最小的滑裂面对应的K=1时，认为边坡即将失稳。该方法还可同时得到与安全系数对应的最危险滑裂面。

根据笔者的计算经验，采用极限平衡判据为主，辅以收敛性判据和突变性判据，是较为可靠和方便的。

三、实例研究

（一）三板溪崩塌体稳定性分析

有关三板溪崩塌体的工程简况参见本篇第十章第七节。

1.刚体极限平衡法分析

刚体极限平衡分析方法很多（陈祖煜，2003），笔者采用Sarma法和剩余推力法（Residual Thrust Method，RTM）进行研究。

将主滑断面上的崩塌体划分为20个条块，如图1-13-1所示。

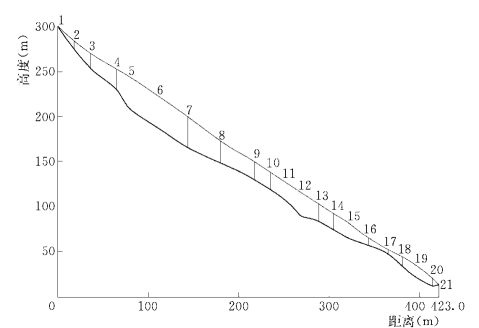
图1-13-1　三板溪崩塌体稳定分析的刚体极限平衡法计算模型

Sarma法计算的安全系数为1.10807，RTM计算的安全系数为1.13809。作为上限解法的Sarma法，其计算的安全系数却比RTM略小。究其原因，是因为滑面坡度较陡，在RTM的计算中，出现了土条之间的剪切力超出极限抗剪强度的不合理现象。

2.块体单元法分析

有关块体单元法的内容参见本书第二篇。

对三板溪崩塌体的稳定性进行块体单元法分析，得到崩塌体的安全系数为1.10。具体计算参见第二篇第七章第四节。

3.有限单元法分析

对三板溪崩塌体的稳定性进行有限单元法分析，得出崩塌体的安全系数为1.03。其他有关应力、变形和屈服情况参见本篇第十章第七节。

表1-13-1　各种方法计算的三板溪崩塌体的稳定安全系数

4.三种方法的比较

将三种方法计算的安全系数汇总，列入表1-13-1。由表1-13-1可以看出，有限单元法计算的安全系数最小，块体单元法与刚体极限平衡法的计算结果相当接近。(www.xing528.com)

笔者还计算了条块之间的相互作用力（图1-13-2～图1-13-4）。在刚体极限平衡法的计算中，这些条间力本身就是中间计算数据，可以直接得到；在块体单元法的计算中，虽然不能直接得到这些信息，但是通过条分面上的应力积分即可得到条间水平推力和条间剪切力；在有限单元法的计算中，可确定各个条分面在有限元网格中的相应位置，然后在这些线段上将应力积分，即可得到条间水平推力和条间剪切力。

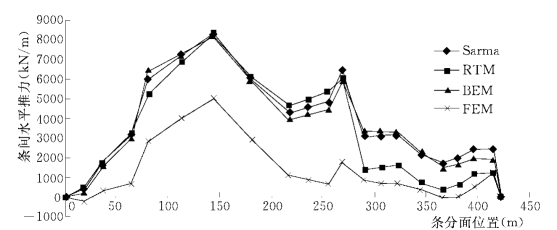
图1-13-2　三板溪崩塌体条间水平推力分布曲线

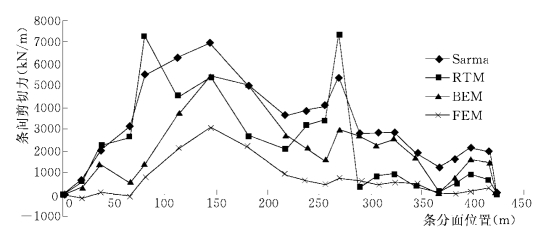
图1-13-3　三板溪崩塌体条间剪切力分布曲线

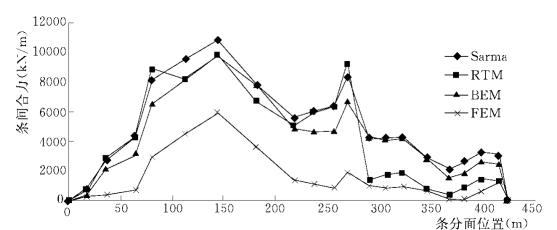
图1-13-4　三板溪崩塌体条间合力分布曲线

图1-13-2表明，各种方法计算的条间推力曲线的形状都比较复杂，但是各条曲线的趋势是基本一致的：在大约144m处，条间推力达到全局极大值；在约217m处，达到局部极小值；在约269m处，又达到局部极大值。对比图1-13-1可知，这三处分别对应7号、9号、12号条分面。在7号和12号条分面处，滑面由陡变缓，上部坡体的下滑力在此得到消减，因而形成了局部极大值；而在9号条分面处，滑面由缓变陡，上部条块下滑受阻，下部条块产生更大的下滑力，条分面有被分离的趋势，因而此处的条间水平推力形成局部极小值。另外，在约367m即17号条分面处，坡体的厚度为全域最小，各种方法计算的此处的条间水平推力亦为最小值。从全域来看，刚体极限平衡法与块体单元法计算的条间水平推力曲线比较贴近，有限单元法计算的条间水平推力偏小。

图1-13-3中条间剪切力的分布规律与条间水平推力相似，但规律性差。

图1-13-4表明，刚体极限平衡法与块体单元法计算的条间合力较为贴近，有限单元法计算的条间合力偏小。

（二）大岩淌滑坡稳定性分析

有关大岩淌滑坡的工程简况参见本篇第十二章第一节。

1.刚体极限平衡法分析

将主滑断面坡体划分为20个条块，如图1-13-5所示。采用Sarma法计算的安全系数为1.41872，采用RTM计算的安全系数为1.42953。与三板溪崩塌体类似，RTM计算的安全系数也比Sarma法略大。

图1-13-5　大岩淌滑坡稳定分析的刚体极限平衡法计算模型

2.块体单元法分析

对大岩淌滑坡的稳定性进行块体单元法分析，得到滑坡的安全系数为1.47。具体计算参见第二篇第七章第四节。

3.有限单元法分析

计算结果详见本篇第十二章第一节。

4.三种方法的比较

将三种方法计算的安全系数汇总，列入表1-13-2。有限单元法计算的安全系数最小，块体单元法的计算结果与刚体极限平衡法较为接近。

表1-13-2　各种方法计算的大岩淌滑坡的稳定安全系数

大岩淌滑坡的条间作用力分布曲线如图1-13-6～图1-13-8所示。

图1-13-6显示的各条间水平推力曲线的变化趋势非常相似。在与10号、13号条分面对应的约336m处、525m处，条间水平推力达到局部极大值。从滑面形状可以看到，这两处的滑面都由陡变缓；在与11号条分面对应的约401m处，滑面由缓变陡，所以此处的条间水平推力为局部极小值。从全域分布来看，有限单元法计算的条间水平推力曲线比其他方法都偏低，刚体极限平衡法与块体单元法的条间水平推力曲线非常贴近。

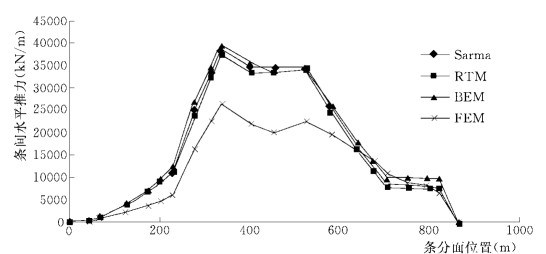
图1-13-6　大岩淌滑坡条间水平推力分布曲线

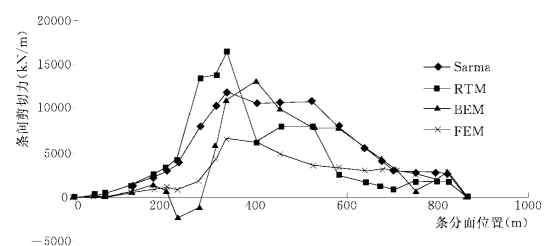
图1-13-7　大岩淌滑坡条间剪切力分布曲线

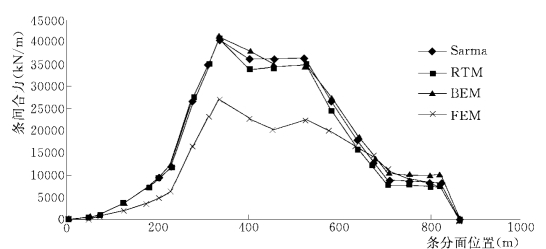
图1-13-8　大岩淌滑坡条间合力分布曲线

图1-13-7显示的条间剪切力的分布规律较条间水平推力差。由于滑面较缓，故相对条间水平推力，条间剪切力普遍很小。

图1-13-8显示的条间合力曲线基本上与图1-13-6显示的条间水平推力曲线的分布规律一致。

四、几点讨论

三板溪崩塌体及大岩淌滑坡是颇具代表性的边坡工程，各具特点：前者坡体狭长且较薄，坡面和滑面陡峭；后者坡体较厚，坡面和滑面平缓。本节分别采用刚体极限平衡法、块体单元法、自适应有限单元法对这两个边坡的稳定性进行了分析比较，从中可以得出一些初步结论：

（1）有限单元法计算的安全系数比本节采用的其他方法都偏低，但各种方法计算的安全系数相差不大。

（2）块体单元法与刚体极限平衡法计算的条间推力比较贴近，而有限单元法计算的条间推力比本节采用的其他方法计算的条间推力都小。

（3）在进行边坡稳定分析时，刚体极限平衡法（如Sarma法等）、块体单元法和有限单元法可以采用大体相同的安全系数取值标准。