后处理模块：可视化技术在有限单元分析中的应用

有限单元分析结果通常包括位移、应变、应力、安全系数、水头、流速等场变量信息，数据量庞大，需借助一些后处理技术来直观地表述各种场变量的分布状态。在后处理过程中，可视化是很重要的一项技术。可视化技术通过计算机，根据数据产生图像，利用颜色、密度、透明度、文字等技术，在短时间内通过图形传递大量信息，使研究人员能够直观、迅速地观察到计算模拟的结果（苏海东，2000；谢春，马兰，彭颖红，2000；袁政强，祝家麟等，2001）。

有限单元分析的特殊性导致其后处理可视化技术也呈现出特殊性——后处理可以借助离散网格来实现，且简洁、高效。有限单元法后处理中的可视化技术包括标量场的可视化技术和矢量场的可视化技术两大类。标量场的可视化方法主要有等值线图、彩色云图、等值面及切片图等，其中以等值线图和彩色云图最为常用；矢量场的可视化方法主要是箭头线段表示法。

以POSTCORE为例，该模块结合有限单元法的特点，利用可视化的相关技术，实现了变位图、矢量场（位移和应力）、等值线、屈服区等的绘制和显示功能。

一、基本理论

1.等值线图

等值线是区域内某场变量量值相等的点连接而成的折线或曲线，在工程分析和计算领域应用很广，如航空测量的等高线地形图、渗流场中的等势线图和流线图、有限单元分析中的相关场变量等值线图等。针对不同的应用领域，产生等值线的算法也不尽相同。

从计算机图形学的角度讲，等值线图具有以下性质：

（1）等值线通常是一条光滑连续的曲线。

（2）对给定的某场变量值Q 0，相应的等值线数量可能不止一条。

（3）由于定义域有界，等值线可能是闭合的，也可能是不闭合的。

（4）等值线一般不相交。

等值线图绘制的难点在于确定等值点的连接顺序，即等值线的游动方向。在已经提出的绘制方法中，比较典型的有追踪绘制法和线性插值扫描法（杨素军，黄培之，1999；孙桂茹，2000；吴鹏，王志坚等2001）。

先将区域离散成单元，再以单元为对象来研究等值线的绘制。离散单元常为三角形和四边形。三角形单元绘制比较简单，但精度较低。本节以四边形单元为例，介绍线性插值扫描绘制等值线的方法，该方法的优点在于可以利用有限单元离散网格和四边形四结点单元各边上场函数线性变化的性质。

设场函数为φ，对某个单元，它的某条边的两结点编号分别为i和j，相应的坐标为（X i，Y i）和（X j，Y j），相应的结点场值为φi和φj。绘制φ=φ0等值线时，等值线通过这条边的条件是

满足该条件时，表示φ=φ0的等值线穿过单元的ij边，等值线和ij边的交点k的坐标由下式确定

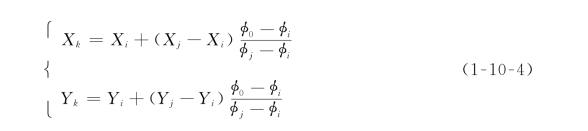
显然，当φ=φ0等值线穿过单元的一条边时，必然穿过单元的另一条边。绘制φ=φ0等值线时，应顺次对域内每个单元的每条边进行扫描，基本步骤如下：

（1）确定该单元的边是否满足式（1-10-3）的条件，若不满足，则扫描下一个单元；若满足，则进入步骤（2）。

（2）按式（1-10-4）确定该单元边和等值线的交点坐标，并统计交点个数。

（3）当交点数为2时，直接连接这两点，就可以得到φ=φ0等值线在该单元中的迹

线；当交点数为4时，需要判断等值线的游动方向。

（4）进行下一个单元扫描。

当全部单元扫描一遍后，即得φ=φ0的等值线图形，包括封闭和不封闭等值线。按一定规律选取等值线的间隔，可得到反映函数场变化的等值线图。用线性插值全域扫描法得到的等值线是由直线段连接而成的折线。可以对这些折线等值线进行光顺（用曲线拟合），但一般情况下当网格相当细时，用直线连接也能得到视觉较好的等值线。

等值线在单元中的游动方向是绘制等值线的难点。当等值线和单元交点个数为4时，可采用线性插值原理来判断等值线的游动方向。(www.xing528.com)

在图1-10-11所示的四结点四边形单元中，四结点的场值依次为φi（i=1，2，3，4），等值线φ0的4个交点为Ii（i=1，2，3，4）。该单元的对角线交点为Q，并假设场值为

由于等值线具有连续性和不相交性，所以I 1和I 3不可能相连；同理，I 2和I 4也不可能相连。因此等值线的连接只有两种情况：

（1）I 1—I 2和I 3—I 4。

（2）I 1—I 4和I 2—I 3。

判断式为

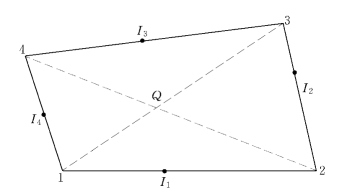
图1-10-11　单元的4个等值点

如果式（1-10-6）成立，表示φ0介于φ1和φQ之间，此时等值线的连接为第（2）种情况；反之，为第（1）种情况。

利用面向对象技术，以单元实体为研究对象，通过C++的多态性，方便地实现了所有单元各类场值等值线的绘制。

2.矢量图

矢量图是另一种常用的场量显示形式，它用大小和方向来描述场量。在有限单元分析中，除描述场值的大小外，常常还需要知道场值的移动方向，如渗流分析中的流速、应力应变分析中的位移等。矢量图能很好地表述这些内容，它需要描述点的位置、场值大小和方向等信息。POSTCORE规定场值的方向为矢量的正向，该方向与X轴正向逆时针构成的角为正角，范围为（0°，360°），矢量大小用一箭头线段表示，线段长度与场值大小有关。

笔者利用一个全局函数Draw Arrow（CDC*p DC，double x，double y，double length，double angle，BOOL b Negtive），实现了场值的矢量化。

3.变位图

变位图描述了实体在内外荷载作用下的变形情况。可以采用一种简单而有效的形式——直接将结点位移按一定的放大比例叠加到结点坐标上，再通过网格变位图来显示实体的变形。

4.屈服区图

屈服区图能直观显示岩体的屈服区域，可以根据屈服区的大小和分布来辅助判断结构的稳定情况。POSTCORE屈服图的绘制通过填充屈服单元实现。

二、模块说明

建立CPost Proc类来解决有限单元法后处理问题。根据面向对象的观点，数据和方法要统一，这样更符合客观实际，又有利于软件系统的稳定。因此，首先应该能得到相关的数据；其次，至少应该具有以下几个方面的功能：①显示变位图；②绘制位移矢量图；③绘制应力矢量图；④绘制等值线图；⑤绘制屈服区图。

同时，为保证相关后处理信息能够被系统记忆，还定义了相关成员的存储和读取功能。

以上是最基本的定义，它能完成一般的后处理，根据需要还可以增加一些新功能。

其中，函数DrawStressVector（）、Draw Disp Vector（）实现了应力矢量、位移矢量的绘制。如前所述，为充分利用面向对象继承和多态的性质，相关等值线的绘制在网格类中实现。函数GetDispData（）、GetStressData（）是数据接口函数。函数Load（CString&str Title）和Store（CString&str Title）分别完成读取和存储相关后处理信息。