实现p型有限单元法的基函数统一化及荷载整合

本节将详细介绍p型有限单元法中的拓扑信息生成方法、边界条件处理方法、刚度矩阵的形成与荷载移植方法，并引入虚结点和广义结点的概念。

图1-9-2　TOPO流程图

一、拓扑信息生成

p型有限单元法的拓扑信息包括：

（1）各结点的坐标。可由手工或网格生成器生成。

（2）各单元的点编号信息。可由手工或网格生成器生成。

（3）各棱的点编号信息。为了p型有限单元法的特别要求，由程序TOPO生成。

（4）各面的棱编号信息。为了p型有限单元法的特别要求，由程序TOPO生成。

（5）各单元的面编号信息。为了p型有限单元法的特别要求，由程序TOPO生成。

TOPO包括3个过程模块（图1-9-2）：各棱的点信息生成模块NODE-EDGE、各面的棱信息

生成模块EDGE-FACE和各单元的面信息生成模块FACE-BODY。

二、边界条件的处理

传统有限单元法把面和棱的约束转化为面和棱上点的约束。由于阶谱单元法中面和棱有各自的基函数，因此对单元贡献了自由度，所以可以看成是虚结点的自由度。这些虚结点的自由度和实结点的自由度同等对待，虚结点和实结点可以统称为广义结点。这样，点基函数、棱基函数、面基函数和体基函数就统一为广义结点的基函数。有了广义结点的概念，许多问题就很容易理解。例如，固定面的约束体现为该面的4个角点为固定约束；该面的棱所代表的虚结点为固定约束；该面所代表的虚结点也为固定约束。其他约束情况可以类推。因为基函数的阶数p＜4时没有面基函数，p＜2时没有棱基函数，故当p＜4时不考虑面的约束，当p＜2时不考虑棱的约束。

图1-9-3和图1-9-4分别表示固定面边界条件和滑动棱边界条件的处理方法，其他情况可以类推。图1-9-3和图1-9-4的各分图中，左图为普通有限单元法，右图为阶谱有限单元法。

三、刚度矩阵的形成与荷载移植

1.单元刚度矩阵

图1-9-3　固定面边界条件处理
（a）p=1；（b）p=2；（c）p=3；（d）p=4(www.xing528.com)

图1-9-4　滑动棱边界条件处理

（a）p=1；（b）p=2；（c）p=3；（d）p=4

于是

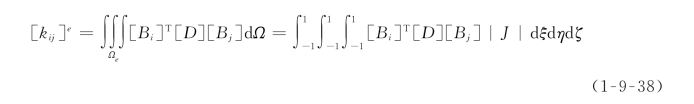
这样，单元刚度矩阵就是阶谱形式。

2.整体自由度的整合

设结构的单元数、实结点个数、棱的个数和面的个数分别为N、N n、N e、N f，则总的结点数为

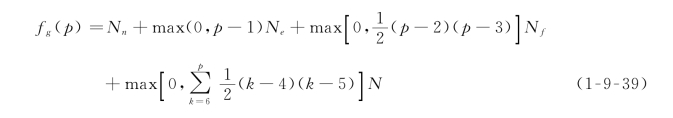
将结构看作点数、棱数、面数和体数分别为N n、N e、N f、N的一个“大的单元”，编排整体结点，并去掉约束所对应的行和列，能使总体刚度矩阵也成为阶谱形式。

3.荷载移植

荷载移植与传统的有限单元法类似，以体力为例，有

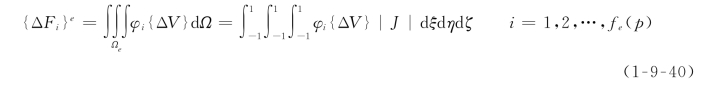
需要注意的是，由于虚结点的存在，移植后的结点荷载与原荷载不存在平衡关系，只是实结点的移植荷载和与原荷载平衡。

对整体自由度进行整合后，整体荷载向量{ΔF}也是阶谱形式。

图1-9-5为刚度矩阵和荷载列阵的阶谱形式。

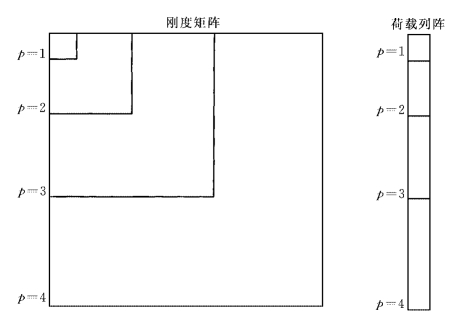
图1-9-5　刚度矩阵和荷载列阵的阶谱形式