节理单元模型及形函数与位移插值的优化方法

为模拟岩体中的结构面，Goodman最早提出了无厚度节理单元的概念（Goodman，Taylor，Brekke，1968）。随后各种有厚度节理单元模型陆续被提出（朱伯芳，1979；王鸿儒，1988）。

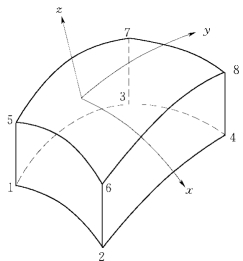
图1-9-1　等厚度的节理单元

一、形函数与位移插值

当结构面的厚度很小或厚度变化不大时，可以分别采用无厚度的节理单元和等厚度的节理单元（图1-9-1）进行模拟。

对节理单元上下面的相应点、棱和面可取相同的点基函数、棱基函数和面基函数，对无厚度节理单元或等厚度节理单元，不存在连接上下两面的棱基函数和面基函数，也不存在体基函数（费文平，陈胜宏，2003）。各基函数的形式为：

（1）点基函数（p≥1）。

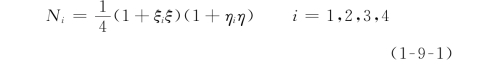
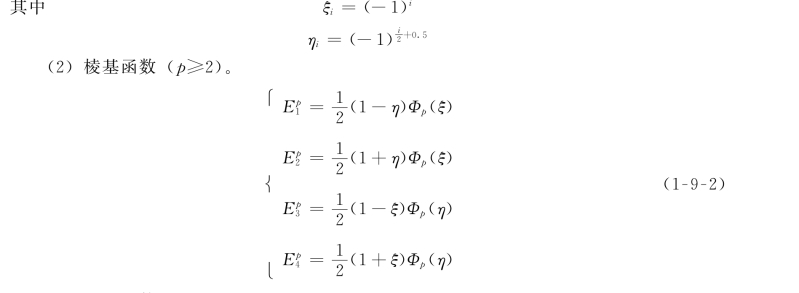
（3）面基函数（p≥4）。

式中：Φp（·）为一切在一维阶谱单元中可行的阶谱基函数。

沿节理单元切线x方向，相应于上、下面的位移差由以下公式给出

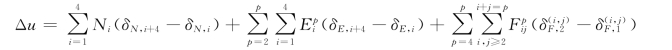
同理，可以写出沿节理单元切线y方向和法线z方向的上、下面的位移差Δv、Δw的表达式。

(www.xing528.com)

式（1-9-4）中，对应于某自由度i的形函数矩阵[N]i是总形函数矩阵[N p]的3×3阶子矩阵。[N p]的定义如下：

当p=1时

二、等厚度节理单元刚度矩阵

由于节理厚度比较小，故其应变只考虑沿节理面的两个剪应变和垂直节理面的一个正应变，并且用节理单元上下面位移差除以节理厚度t来表示，即

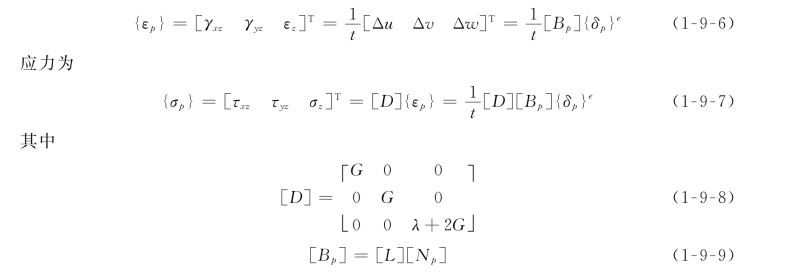
式中：[D]为弹性矩阵；[B p]为单元应变矩阵；[L]为坐标转换矩阵。

定义整体坐标系的X轴朝北，Y轴朝西，Z轴朝上；定义节理单元的局部坐标系的z轴为中面的法线朝上方向，y轴指向节理面的倾向，x轴由右手法则确定（图1-9-1）；设节理的倾角为θ，倾向为φ。则式（1-9-9）中的坐标转换矩阵[L]为

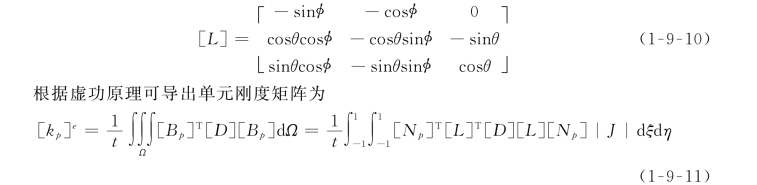
三、无厚度节理单元刚度矩阵

当等厚度节理单元的厚度t→0时，即形成无厚度节理单元。此时，引入节理的法向刚度系数和切向刚度系数k n、ks，重新定义节理的弹性矩阵为

并定义弹性应力应变关系为

则单元刚度矩阵式（1-9-11）保持不变。