p型有限单元法与传统有限单元法相比,在数值计算方法方面(主要是数值积分和方程组的解法)有其自身的特点(Tsuji,Carnevali,1992;Carnevall,Morris,Tsuji,Taylor,1993;Hinnant,1994;Morris,Papadrakakis,Babilis,1994;陈新度,余俊,周济,1997;程昭,陈胜宏,1999;王周宏,胡于进,1999)。
一、数值积分
有限单元法中,数值积分主要采用高斯积分方法。当阶数升高时,基函数将是高阶多项式,为保证精度,需要更多的积分点,从而使运算量大大增加,三维问题尤为突出。有些文献认为,p型有限单元法由于运算量随着p的增大而急剧增加,其使用将十分有限,p不会超过4。为避免这种瓶颈现象发生,下面介绍一些减少运算量的措施和一种新颖的矢量积分法。
(一)减少积分运算量的措施
这种措施主要针对高斯积分方法,以单元刚度矩阵为例,其中的一个子块为
![]()
把本章第一节中定义的点基函数、棱基函数、面基函数和体基函数统一记为φi[1≤i≤f e(p)],则式(1-8-125)中的应变矩阵为
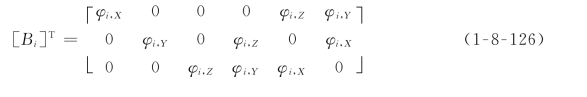

利用阶谱单元的特点,减少高斯积分运算量的措施有:
(1)充分利用[B]的稀疏性,对于弹性问题,还可以利用[D]的稀疏性。将[Bi]T[D][Bj]的各个元素先进行代数运算,再对各个元素进行数值积分。
(2)单元刚度矩阵的不同元素采用不同阶高斯积分来计算。实际上,如果对高阶阶谱单元的各个元素全部采用高阶高斯积分,则计算时间将难以接受。
(3)另外,从基函数的构造可以看到,即使一个方向上的阶数很高,另两个方向上的阶数可能很低,因此不同方向上也可以采用不同阶的高斯积分。
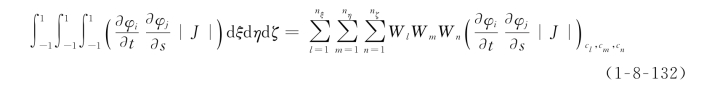
式中:cl、cm、cn为高斯点;W l、W m、W n为高斯权重。
设p(f,τ)表示函数f在τ方向上的阶数,则有
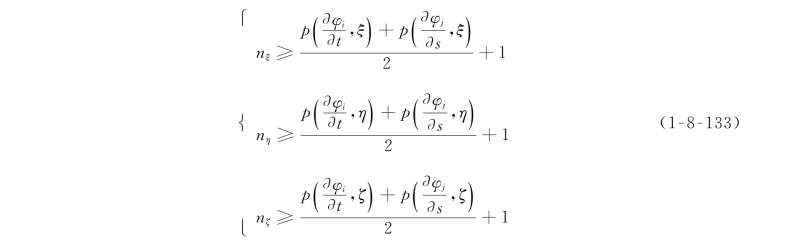
单元刚度矩阵形成时间比较见表1-8-1。
表1-8-1 单元刚度矩阵形成时间比较单位:s

注 使用PⅡ233微机。
表1-8-1表明,措施(3)能在措施(2)的基础上进一步大大减少运算时间,当阶数较高时,运算时间甚至能减少90%以上。
(二)矢量积分法
矢量积分法利用了p型有限单元法的阶谱特点,其运算代价比高斯积分法小。下面以一维矢量积分法为例进行说明。
1.矢量积分法基本原理
单元刚度矩阵一般可以表示为如下形式
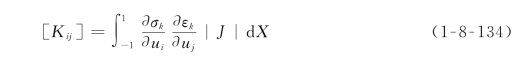
式(1-8-134)表明,单元刚度矩阵是两个函数的点积的积分,其中一个只和行标i有关,另一个只和列标j有关(雅可比行列式可并入任一函数),故可将式(1-8-134)改写成下面的简单形式
![]()

函数g(X)和h(X)的勒让德级数表示式为

这里,I的范围是从0到某一适当的奇数m,且n=(m+1)/2。权函数W j与正交多项式的阶数I、积分点X j以及积分点的个数n有关。
2.积分点的选择
对积分点具体位置的优劣评价还有待进一步研究,一个较好的系列是
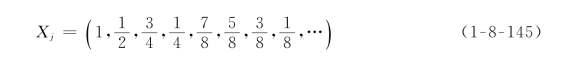
式(1-8-145)的优点是,在积分过程开始后,可以先试算前面的几个积分点,如果达不到要求的精度,可以再加算一些点,先前的计算并没有浪费。这种方案即所谓的自适应型。
其他可行的积分位置包括Gauss-Legendre、Gauss-Lobatto等系列。
3.权函数的计算(https://www.xing528.com)
(1)当I是偶数时。由式(1-8-143)和式(1-8-142)得



二、线性方程组的解法
p型有限单元法形成的线性方程组
![]()
有如下的特点:
(1)[A]是大型对称稀疏正定矩阵。
(2)[A]的非零元素随机分布。
(3)[A]和{b}具有阶谱特点。
下面首先介绍求解方程的对称逐步超松弛预处理共轭梯度法,简称SSOR-PCG解法,这种方法比较适合具有前两个特点的方程组;然后介绍其改进的迭代格式;最后结合特点(3),给出适合p型有限单元线性方程组的完整解法。
1.SSOR-PCG解法(吕涛,石济民,林振宝,1992)
设[M]=([S]T[S])-1为对称正定矩阵,则式(1-8-159)等价于
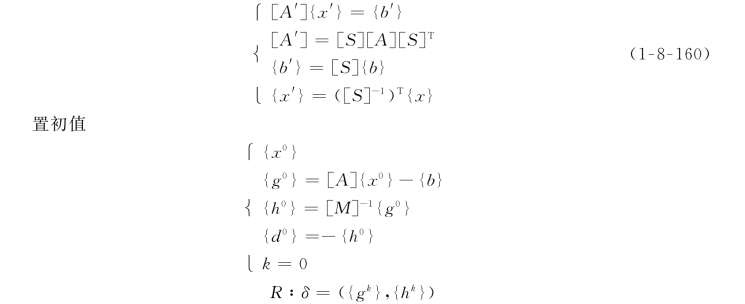
如果δ≤ε,则停止,否则
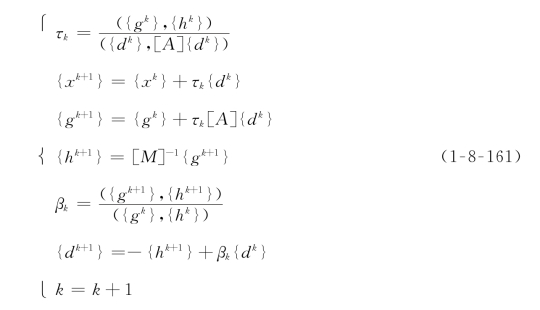
转到R。
等价问题式(1-8-160)的收敛速度取决于条件数Cond([A′])。若[M]为单位矩阵,则式(1-8-161)为原问题的共轭梯度法(CG)的迭代格式,其收敛速度取决于Cond([A]),每步迭代的主要计算量为(ra+5)n次乘法运算。这里ra为[A]的各行非零元素个数的平均值。通常Cond([A])相当大,因此希望Cond([A′])≪Cond([A])。如此选择的[M]称为[A]的预处理矩阵。好的预处理矩阵应满足如下条件:
(1)Cond(A′)≪Cond(A)。
(2)相对于[A],不要求过多内存。
(3)解方程[M]{h}={g}较解方程[A]{x}={b}远为容易。
当[M]取为对称逐步超松弛迭代法(SSOR法)的分裂矩阵时,即
![]()
可以满足上述条件。
式中:ω为松弛因子,且0<ω<2;[D]为[A]的对角矩阵;[L]为[A]的严格下三角矩阵。
![]()
此时对式(1-8-160)实施CG算法,即称为SSOR-PCG法。
在SSOR-PCG法中,计算{h}=[M]-1{g}相当于三角分解法中的前代与回代过程,或者等价于用SSOR法迭代一次。因此实际计算时,不必对[M]求逆,也不必另开辟数组存放矩阵。计算[A]{d}和求解[M]{h}={g}仅对[A]的非零元素进行运算,所以仅需储存[A]的下三角矩阵中的非零元素。若将{h}和{d}放大同一倍数,迭代格式仍然适用。因此,[M]中的2-ω可不参加计算。该法每步迭代的主要计算量为(2ra+6)n次乘法运算,其中(ra+1)n次用于计算{h}=[M]-1{g},ran次用于计算[A]{d}。
林绍忠(1997)及其他一些研究者进一步提出了对SSOR-PCG解法的改进格式。
2.升阶加速方案
上述SSOR-PCG解法及其迭代格式是一种普遍的解法,并未考虑[A]和{b}的阶谱特点。考虑阶谱特点后,可以充分利用低阶时已经计算出来的方程组的解。
(1)迭代方法。设p阶时方程组为

式中:s为在每次重分析过程中的迭代次数。
计算经验表明,这种迭代方法收敛很快,一般不超过5次。
(2)初值法。初值法是一种更方便、更直接的加速方法。设p-1阶时方程组的个数为n p-1,当升到p阶后,方程组的个数为n p=n p-1+n a。令式(1-8-161)中{x 0}为

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




