离散误差估计和自适应升阶方法

自适应有限单元法的一个重要内容是离散误差估计（Babuska，Rheinboldt，1978；Babuska，Rheinboldt，1979；Babuska，Rheinboldt，1989；Babuska，Strouboulis，Upadhyay，1994；Babuska，Strouboulis，1994）。h型离散误差的估计方法已经比较成熟，p型离散误差估计方法还有待进一步发展。本节以应力应变分析为例，在有限单元法离散误差估计理论的基础上，依次介绍3种不同类型的p型有限单元离散误差估计与自适应升阶方法。

一、离散误差估计的基础理论

1.离散误差范数

一般的线弹性问题的描述见式（1-6-1）～式（1-6-3）。在某个固定网格下，若取单元插值基函数的阶数为p，记{u p}、{εp}、{σp}为有限单元计算结果，{u}、{ε}、{σ}为精确解，则误差向量为

定义误差的能量范数为

常用能量范数形式对误差进行度量，在弹性条件下，有

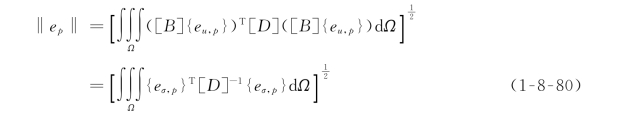
能量范数并非是衡量离散误差的唯一形式，另一种可行的形式是L 2范数，包括位移和应力两种形式，分别为

式中：‖e p‖i为单元i的离散误差。

应该指出，这几种离散误差范数结构相似，差别不大，所以如果不作特别说明，一般指能量范数。

按式（1-6-17）定义精确解的总能量范数后，相对误差即可用式（1-6-18）表示。

2.收敛速度

自适应有限单元法中的h型方法、p型方法和hp型方法的收敛速度不尽相同。

（1）h型方法。

式中：N为方程组的自由度；C 1、C 2为依赖于解的光滑程度的正常数。

如果离散误差大致均匀地分布于各个单元，则这时的网格称为最优网格，其对应的最优收敛速度为

（2）p型方法。式（1-8-84）也适用于p型方法。

当奇点仅在边界上时，收敛速度为

式中：β为依赖于解的光滑程度的一个正常数。

（3）hp型方法。结合h型和p型两种方法，可以达到指数函数形式的收敛速度，即

式中：C 3、γ和θ均为正常数，且θ≥1/3。

二、全域升阶方法

研究表明（Zienkiewicz，Irons，Scott，and Cambell，1970；Zienkiewicz，De，Gago and Kelly，1983），误差的应变能U随着网格的加密或插值函数阶次的升高，将单调趋于零。对p型自适应问题，由误差能量范数式（1-6-7）的定义，有

U(u p-u)=‖u p-u‖2(1-8-88)

现在的问题是如何估计精确解的能量范数。根据现有的研究成果，大体有两种方法：误差理论方法和实用方法。

1.误差理论方法

在网格划分比较合理的情况下，p型有限单元的收敛速度为

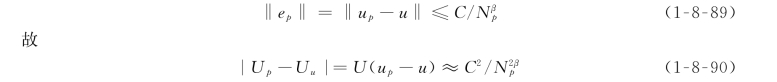
式中：N p为自由度。

式（1-8-90）中有U u、C和β共3个未知数，求解的前提是至少有3个方程。考虑到

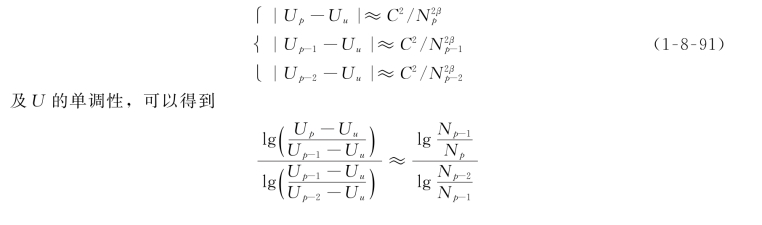
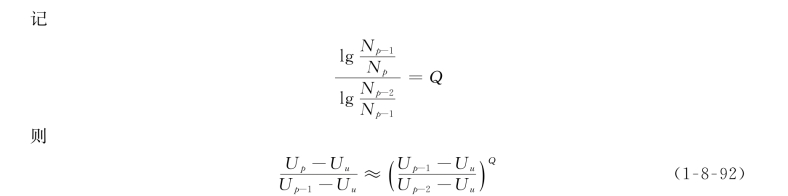
由式（1-8-92），可以估算出精确的应变能U u。

从以上推导可以看出，严格意义的全域升阶需至少先进行连续三阶的p型有限单元计算，然后根据估计的精确解的应变能U u和误差应变能U（u p-u）计算当前误差，即

当e≤et时，自适应计算结束，否则需继续升阶。

2.实用方法

以上根据有限单元误差理论的方法需至少先进行连续三阶的p型有限单元计算。由于在计算岩体力学中，研究自适应技术的主要目的是使软件规范化而不是片面追求精确，因此，笔者建议以下实用方法：(www.xing528.com)

（1）对整个计算域，假定已经有p阶计算结果，升高一阶，即对p+1阶进行计算。

（2）直接把高一阶的结果{σp+1}作为精确解的最佳猜测，定义相对误差为

（3）当e≤et时，自适应计算结束，否则令所有单元p=p+1，并重复以上过程。

使用全域升阶法，当有奇点时怎样划分网格才比较合理呢？Szabo（1986）建议趋向奇点的网格尺寸大小的比例系数为0.15（图1-8-10）。

三、单元升阶方法

全域升阶方法虽然比较精确，但需合理地划分网格，即在应力变化比较剧烈的地方，网格应该划分得密集一些。但在不知道应力分布的情况下，网格划分的合理性是不容易掌握的。于是，在某些应力变化不怎么剧烈的地方，单元插值函数的阶次也被迫升高，显然是不经济的。为此，下面介绍p型有限单元升阶方法。它的升阶考察对象局限于某一个单元，避免了处于应力变化比较平坦区域单元的不必要的升阶。

在单元升阶方法中，估计精确解的能量范数同样有两种方法：误差理论方法和实用方法，且都可以在单个单元的基础上进行计算。

1.误差理论方法

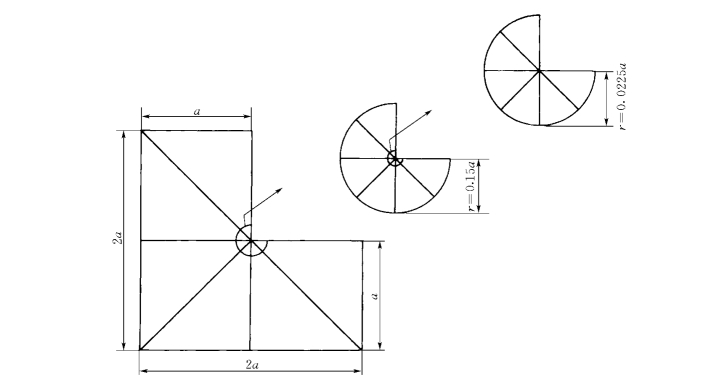
图1-8-10　有奇点时的网格设计

其中，φ是0到1之间的任何一个减缩系数。例如，如果β允许有25%的误差，则φ=1/1.25=0.8。

在满足式（1-8-95）的情况下，升阶到p+1时，自然有

同样，阶次为p+n时，可得到

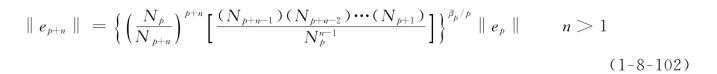
利用式（1-8-102）可以预测某一给定单元在不同阶次时的能量范数误差，这种单元的结点要求不能为奇点。

当单元的某结点为奇点时，β=λ为常数，其中λ决定于奇点的强度。采用上述类似的方法，有

2.实用方法

（1）对某个单元i，假定已经有p阶计算结果，升高一阶，对p+1阶进行计算。

（2）直接把高一阶的结果{σp+1}i作为精确解的最佳猜测，定义单元i的相对误差为

（3）当ei≤et时，保持p不变，否则令该单元p=p+1。对所有单元进行此项判断。

（4）重复过程（2）和过程（3），直到对所有单元均满足

四、自由度升阶方法

即使是采用单元升阶方法，给定单元升阶也有可能引入不必要的自由度，即引入的某些自由度对提高有限单元解的精度贡献不大。为此，可以进一步引入基于自由度意义上的升阶方法。

另外，不管使用何种方法来估计有限单元法的离散误差，由于有限单元法的精确解实际上不可知，所以总要假定一个较为精确的解来代替精确解。例如，重新划分成较为精细的网格或引入较高阶次的单元插值函数得到一个新解，这两种方法都要重新求解一个新的线性代数方程组。从本小节可以看到，在p型自适应分析中，为得到较为精确的有限单元解，重新求解一个新的线性代数方程组并不是必须的。

把常规的有限单元方程写为升阶形式，即

一个可行的假定是

另一种可能是和余量联系在一起。式（1-6-1）的微分方程精确解和有限单元解应该产生一个余量

注意到式（1-8-110）中第二式实际上是加权余量的形式

这时，式（1-8-120）相应地改进为

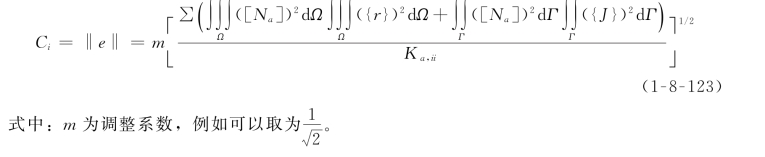
自由度升阶方法是仅引入那些使Ci比较大的自由度。例如，使下一个升阶步增加的自由度满足

显然，γ=0就表示全域升阶方法。经过若干升阶步后，大于零的γ将使各单元的离散误差趋于相等。根据计算经验，如果γ＜10%，则有可能使下一个升阶步引入对提高有限单元解的精度不重要的自由度；如果γ＞25%，则有可能使下一个升阶步增加的自由度不够最低限度。故一般取：10%≤γ≤25%。

自由度升阶方法的突出特点是：可以用最经济的自由度达到要求的精度。当然通常要进行若干个升阶步才能达到要求的精度。