传统的C0型单元的插值基函数具有以下性质:①每个插值基函数在自己所对应的结点上等于1,在其他结点上等于0;②所有基函数之和等于1。这类单元的缺点是:当低阶单元升为高阶单元时,低阶单元的各个基函数也都随之变化。这将为通用程序的编制带来不便,特别是不适合于p型自适应有限单元的分析。在p型自适应有限单元分析中,当发现利用较低阶单元对某问题进行分析的精度不满足预定的要求时,需在单元网格划分不变的条件下提高单元的阶次,并希望已形成的低阶单元的刚度矩阵保持不变地被利用。显然,采用传统的单元不可能实现上述希望。本节所讨论的阶谱单元可以克服这个缺点。
以H pi表示单元尺寸不变时p i阶阶谱单元逼近空间,阶谱的概念是低阶单元逼近空间是高阶单元逼近空间的一个子集,即
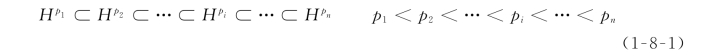
因此,低阶单元刚度矩阵是高阶单元刚度矩阵的子块。当为提高精度而升阶时,可以利用已经计算出来的低阶单元刚度矩阵。
在阶谱单元中,由于结点参数不一定都具有结点函数值的物理意义,因而原来传统型单元插值基函数所具有的某些性质现在不再保持。例如,单元的插值基函数的和不再等于1。但是单元的收敛性质并未改变,因为单元内部函数的插值表示的实质并未改变。
一、一维阶谱单元及其基函数
1.基本概念
最基本的传统C0型一维单元为
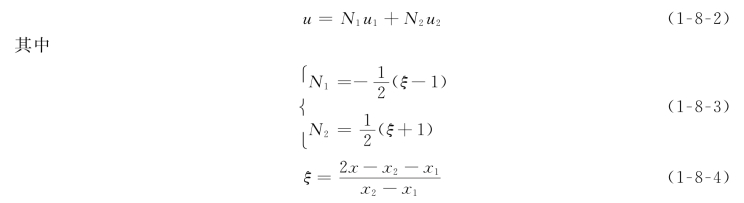
式中:x 1为单元左端结点的整体坐标值;x 2为单元右端结点的整体坐标值;ξ为局部坐标。
上述定义意味着ξ是一个原点位于单元中点的无因次量,其在单元两端的值分别为-1和1(图1-8-1)。
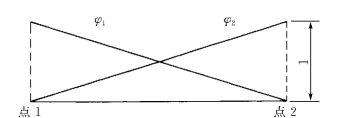
图1-8-1 传统一维单元及其基函数
以上是插值函数阶次为1的单元。这时,阶谱单元和传统单元的基函数完全一样。
当插值函数的阶次为2时,传统单元的基函数为
![]()
其中
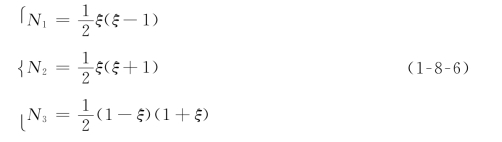
u 1、u 2和u 3具有明确的物理意义,它们分别表示单元的左端点、右端点和中点的结点参数;N 1、N 2和N 3具有拉格朗日插值函数的特点,即在本点值为1,在其他点值为0,并且和为1。比较式(1-8-3)和式(1-8-6)可以看出,低阶单元的单元矩阵并不是高阶单元的单元矩阵的子阵。因此,对于一个既定的有限单元网格,如果为了改善结果精度而想用高阶单元来代替低阶单元重新进行计算,则全部计算工作必须重新开始,这自然是不经济的。
阶谱单元保持式(1-8-5)和式(1-8-2)中的N 1与N 2不变,即N 1与N 2由式(1-8-3)决定,而插值函数则可写为
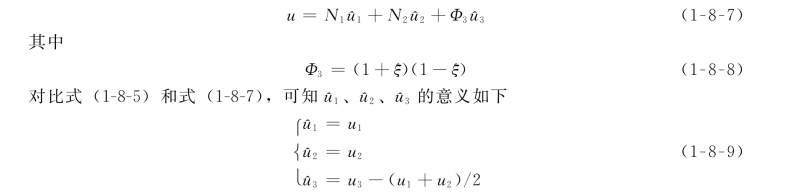
式(1-8-9)表明,阶谱单元中,结点参数不一定具有结点函数值的物理意义。因而原来传统型单元插值函数所具有的性质不再保持。例如,N 1、N 2在单元中点(ξ=0)不再等于0,同时所有单元插值函数之和也不再等于1。但是应该指出,单元的收敛性质并未改变,因为只是重新定义了第3个结点参数的意义为^u 3=u 3-(u 1+u 2)/2,而单元内函数u的插值表示的实质并未改变。
需要指出的另一点是,阶谱函数Φ3在以上的讨论中采用了1-ξ2的形式,但这并非唯一可能的选择。实际上只要是在结点1、2保持为0的任意一个二次函数都是可能的选择。在实际分析中,对结点参数的理解也不一定非要和某个物理量相联系。
循上述思路,如果将一维二次单元升阶为三次单元,那么保持阶谱基函数N 1、N 2和Φ3不变,只要求新增加的Φ4是在结点1、2等于0的一个三次函数即可。例如
![]()
按上述思路继续下去,可以构造更高阶的阶谱基函数。例如

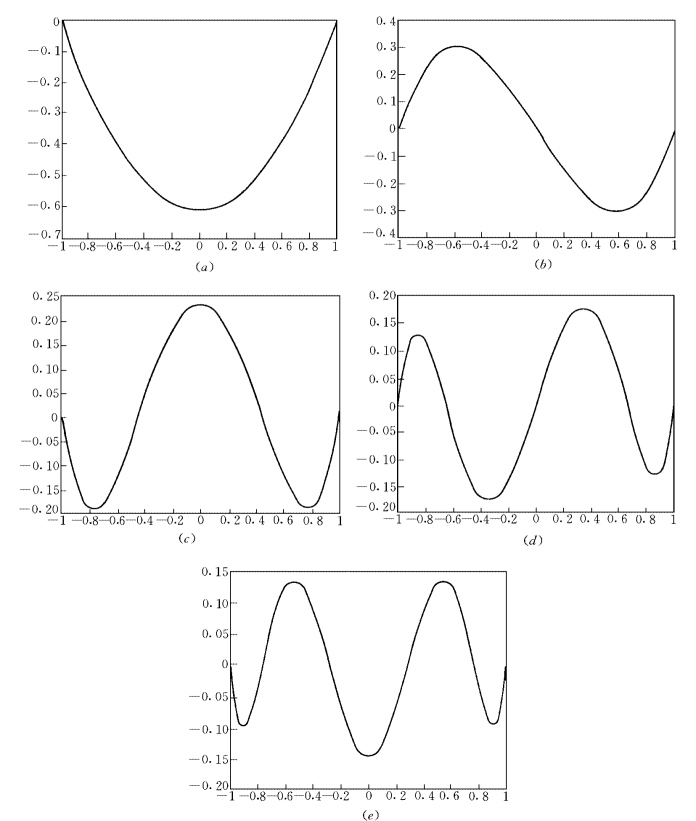
图1-8-2 勒让德正交多项式曲线图
(a)-Φ3;(b)-Φ4;(c)-Φ5;(d)-Φ6;(e)-Φ7
雅可比正交多项式的函数图与勒让德正交多项式的函数图非常相似。
3.基于正交多项式的阶谱基函数的优点
以拉压杆单元为例,其刚度矩阵为

利用式(1-8-13),可计算得

式中:E、A、l分别为杆单元的弹性模量、断面面积和长度。
可以看出,除了常应变项外,单元的刚度矩阵是一个对角矩阵,可以节约计算机内存和加快计算速度。
此外,基于正交多项式的基函数形成的刚度矩阵还具有条件数小的特点。
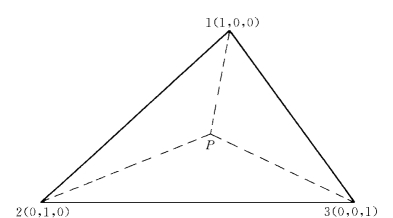
图1-8-3 三角形单元的单形坐标
二、二维阶谱单元及其基函数
二维阶谱单元的基函数包括点基函数、棱基函数和面基函数。点基函数满足在本点值为1,在其余各点值为0的条件;棱基函数满足在本棱的端点处值为0,在其余各棱上的值为0的条件;面基函数满足在本面的棱边上值为0的条件。面基函数在二维问题中有时也称为内部基函数。
1.三角形阶谱单元及其基函数
对于二维三角形,面积坐标是单形坐标,定义如下(图1-8-3):

显然,ξ1、ξ2、ξ3的范围是[0,1],且ξ1+ξ2+ξ3=1。
类似于一维单元,可定义:
(1)点基函数。
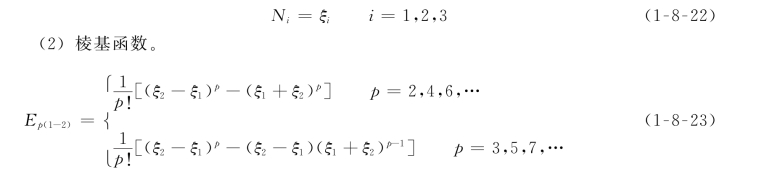
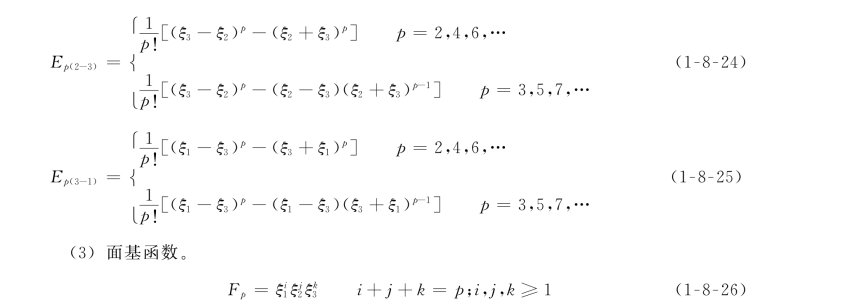
也可以采用基于雅可比正交多项式的三角形阶谱单元,此时可定义:
(1)点基函数(p≥1)。
![]()
(2)棱基函数(p≥2)。
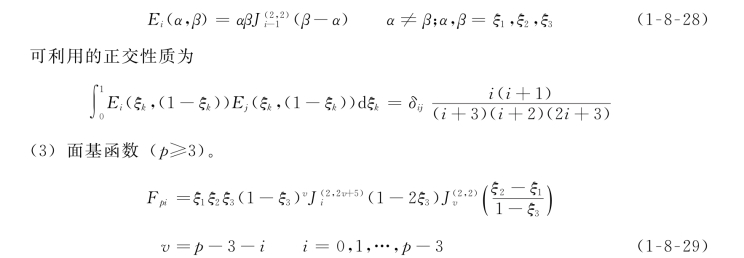
可利用的正交性质为
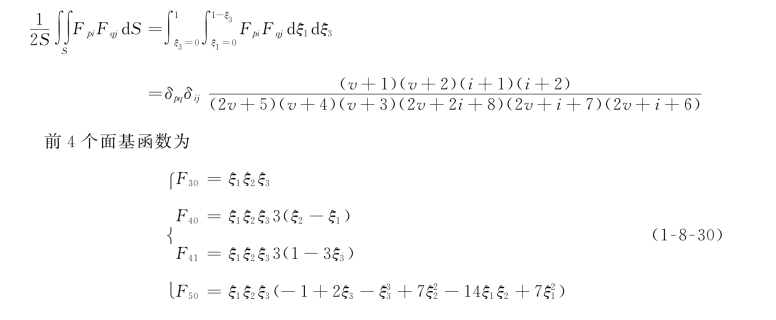
基于雅可比多项式的前4个面基函数如图1-8-4所示。
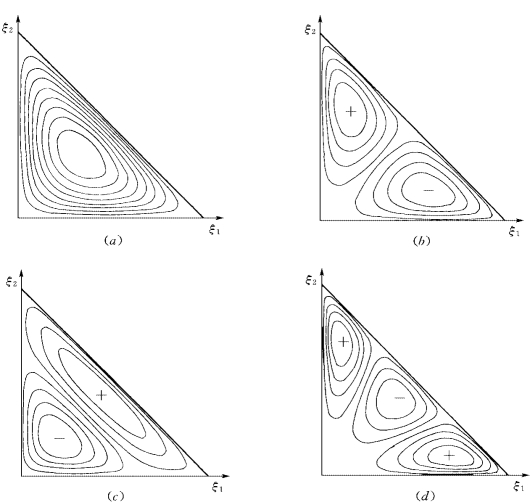
图1-8-4 基于雅可比多项式的前4个面基函数
(a)F 30;(b)F 40;(c)F 41;(d)F 50
2.四边形阶谱单元及其基函数
任何四边形都可以映射成标准母单元(图1-8-5)。
(1)点基函数(p≥1)。(https://www.xing528.com)
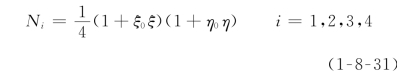
其中
![]()
![]()
式中:ξ0、η0为i点在母单元坐标系中的坐标。
(2)棱基函数(p≥2)。
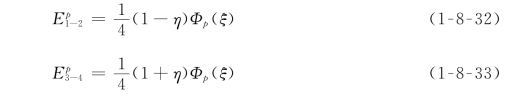
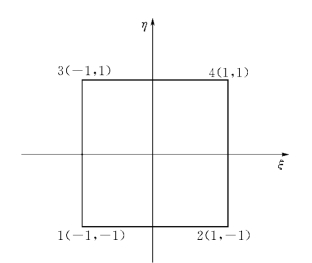
图1-8-5 四边形母单元
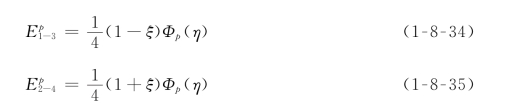
式中:Φp为一切在一维阶谱单元中可行的阶谱基函数。
(3)面基函数(p≥4)。
![]()
以上相当于Serendipity族基函数。如果不限制面基函数i+j=p,而将其改为i,j≤p,即相当于Lagrange族基函数。Serendipity族基函数比Lagrange族基函数个数少,能减轻计算量。基函数曲面图及等值线图如图1-8-6所示。
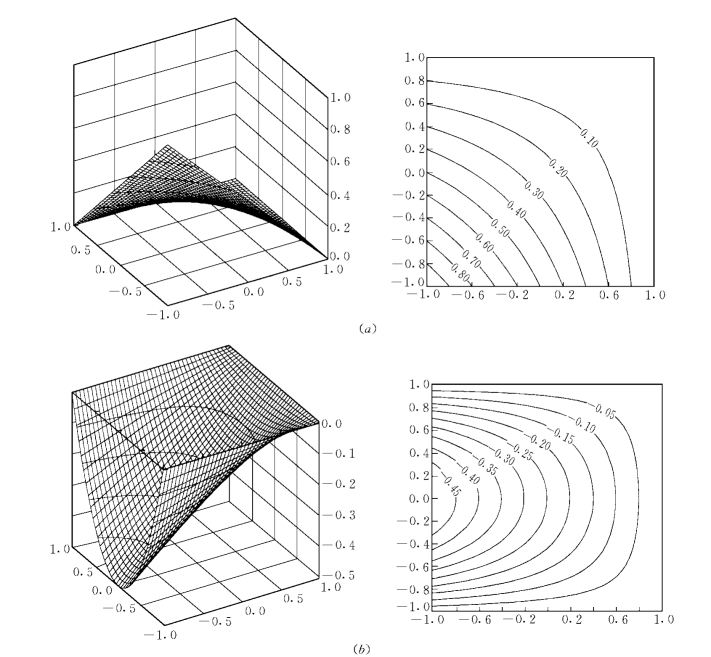
图1-8-6 基函数曲面图及等值线图(一)
(a)点基函数(Ni);(b)棱基函数(E 2i)

图1-8-6 基函数曲面图及等值线图(二)
(c)棱基函数(E 3i);(d)棱基函数(E 4i);(e)面基函数(F 4(2,2))
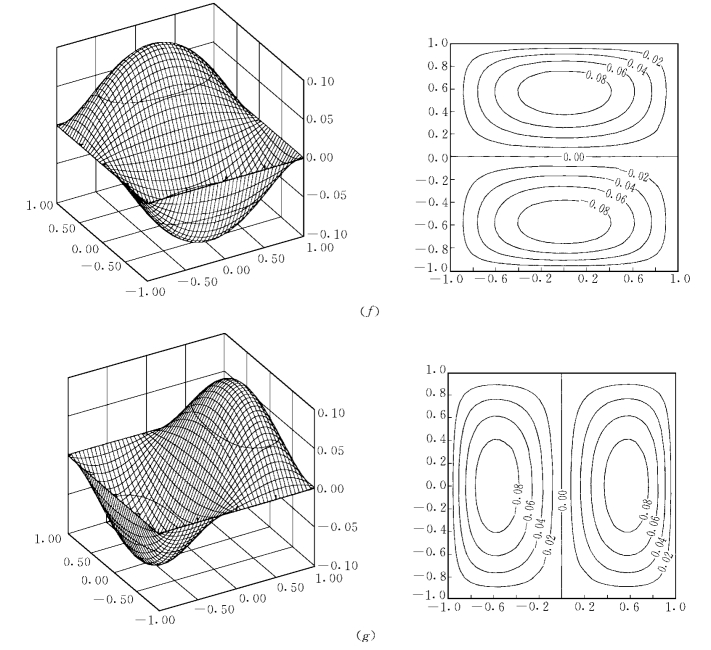
图1-8-6 基函数曲面图及等值线图(三)
(f)面基函数(F 5(2,3));(g)面基函数(F 5(3,2))
三、三维阶谱单元及其基函数
三维阶谱单元的基函数包括点基函数、棱基函数、面基函数和体基函数。点基函数满足在本点值为1,在其余各点值为0的条件;棱基函数满足在本棱的端点处值为0,在其余各棱上的值为0的条件;面基函数满足在本面的棱边上值为0,在其余各面上的值为0的条件;体基函数满足在各面上的值为0的条件。体基函数在三维问题中有时也称为内部基函数。
1.四面体阶谱单元及其基函数
对于三维四面体,单形坐标是体积坐标,定义如下(图1-8-7):
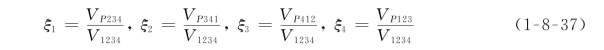
(1)点基函数(p≥1)。

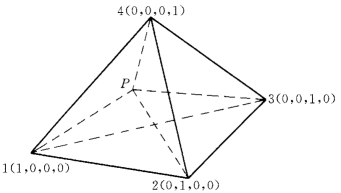
图1-8-7 四面体单元
前几个棱基函数为
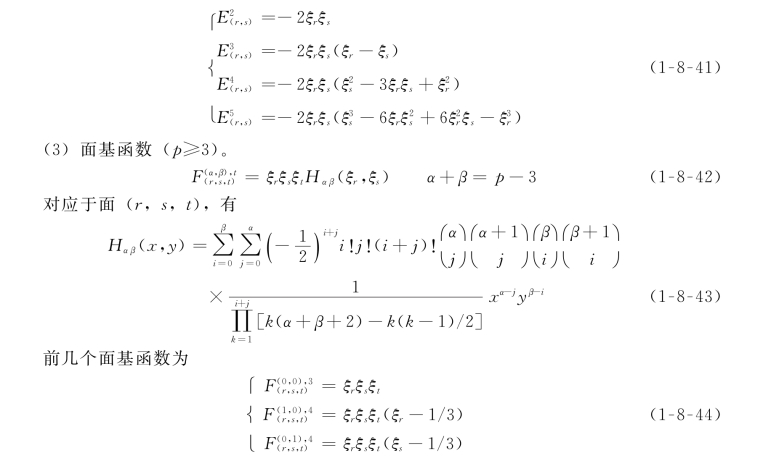
(4)体基函数(p≥4)。
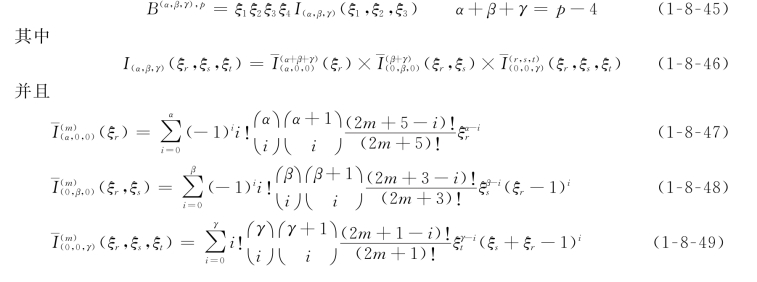
前几项体基函数为
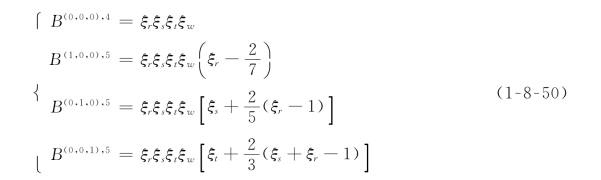
2.六面体阶谱单元及其基函数
任何六面体都可以映射成标准母单元(图1-8-8)。
(1)点基函数(p≥1)。
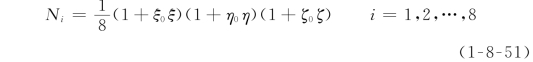
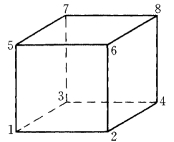
图1-8-8 六面体母单元
式中:ξ0、η0、ζ0为i点在母单元坐标系中的坐标,有
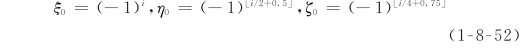
(2)棱基函数(p≥2)。

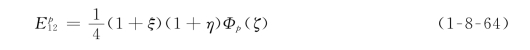
式中:Φp为一切在一维阶谱单元中可行的阶谱基函数。
(3)面基函数(p≥4)。
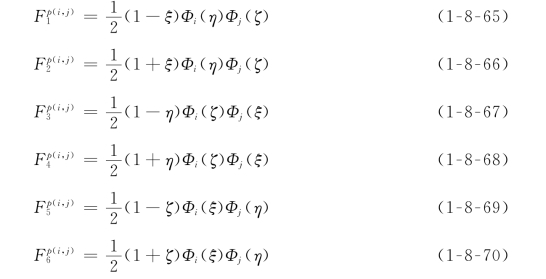
式(1-8-65)~式(1-8-70)中,i、j≥2,i+j=p。
(4)体基函数(p≥6)。
![]()
以上相当于Serendipity族基函数。同样,如果不限制面基函数i+j=p和体基函数i+j+k=p,而将其分别改为i、j≤p和i、j、k≤p,即相当于Lagrange族基函数。
3.三棱柱体阶谱单元及其基函数
在底面上使用单形坐标,即面积坐标ξ1、ξ2、ξ3,范围[0,1];在侧棱方向映射成一维母单元坐标t,范围[-1,1]。如图1-8-9所示。
(1)点基函数(p≥1)。
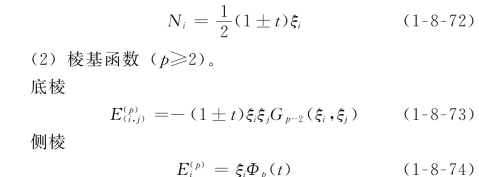
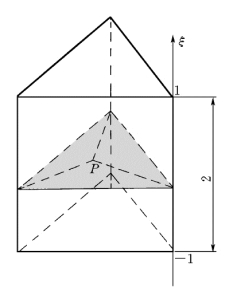
图1-8-9 三棱柱体单元
(3)面基函数。
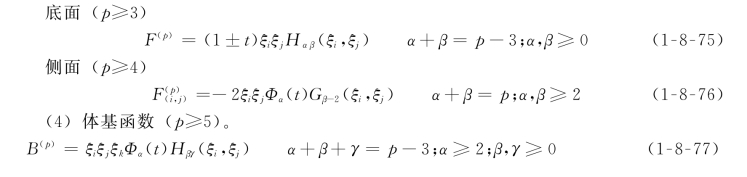
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




