一、土坝渗流:二维问题
考察一个有水平排水的均质土坝(图1-7-2),输入初始背景网格尺度h=5m,产生背景网格(图1-7-3)的误差为e=17.2%,指定允许网格离散误差et=10%后,经两个循环,网格达到最优,实际误差e=9.7%(图1-7-4)。表1-7-1列出了在排水起点处渗透坡降J随网格精度的变化情况,由于J是土坝渗透破坏的主要评判指标,可见控制网格精度非常重要。
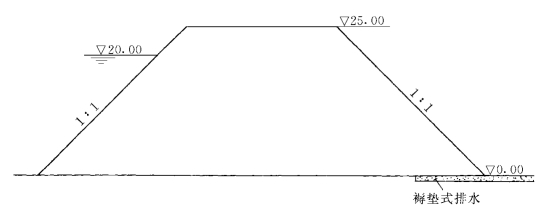
图1-7-2 有水平排水的均质土坝(单位:m)
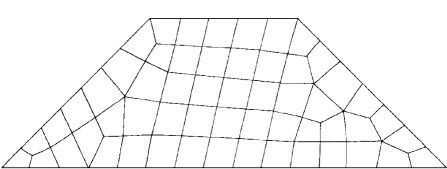
图1-7-3 初始背景网格(56个单元,74个结点)
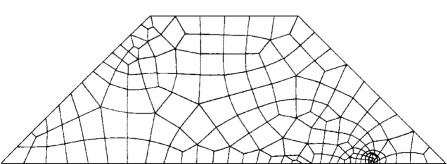
图1-7-4 优化网格(198个单元,232个结点)
图1-7-5给出了采用有限单元法和解析法(波庐巴里诺娃-柯琴娜,1957)得到的自由面,图1-7-6是优化网格下的渗流场。
表1-7-1 不同网格误差下排水起点的渗透坡降值

二、均质闸基:三维问题
闸底板不透水的均质闸基,上游水头5.0m,下游无水(图1-7-7)。这是一个有压渗流问题,不需进行自由面的迭代。
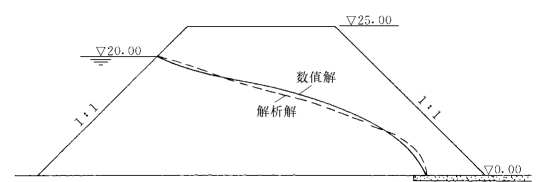
图1-7-5 自由面(单位:m)

图1-7-6 优化网格下的渗流场(单位:m)
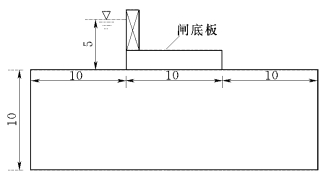
图1-7-7 闸基算例(单位:m)
输入初始均匀网格尺度h=3.0m,调用网格生成器GENSEEP生成初始均匀网格,其消隐图如图1-7-8所示。在初始均匀网格下用SEEP进行渗流有限单元计算。DENSEEP计算结果表明,网格离散误差达e=31.1%。指定允许误差et=10%,经过2个循环,网格达到最优,最终实际误差为e=9.3%。优化网格的消隐图如图1-7-9所示,各次计算的网格误差见表1-7-2。图1-7-10是优化网格下顺河床方向剖面的压力水头等值线图,图1-7-11是优化网格下该剖面的流速场。(https://www.xing528.com)
表1-7-2 各次计算的网格误差

三、均质土坝:三维问题
坝基不透水的均质土坝,上游水头15.0m,下游水头5.0m(图1-7-12)。
输入初始均匀网格尺度为h=5.0m,调用网格生成器GENSEEP生成初始均匀网格,其消隐图如图1-7-13所示。用SEEP进行渗流有限单元计算。DENSEEP计算结果表明,初始网格离散误差达e=37.2%。指定允许误差et=10%,经过3个循环,网格达到最优,最终实际误差为e=8.0%。优化网格的消隐图如图1-7-14所示。
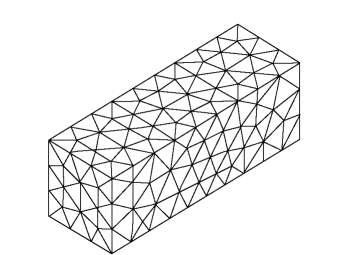
图1-7-8 初始均匀网格消隐图(797个单元,236个结点)
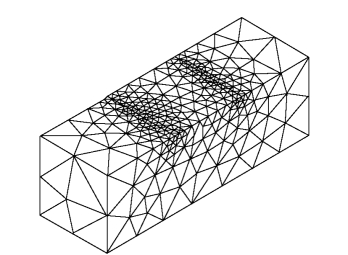
图1-7-9 优化网格消隐图(2397个单元,621个结点)
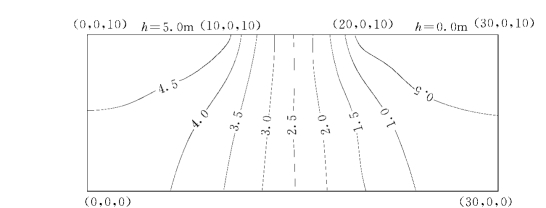
图1-7-10 优化网格下顺河床方向剖面水头等值线
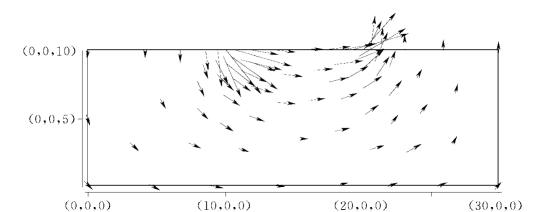
图1-7-11 优化网格下顺河床方向剖面流速场
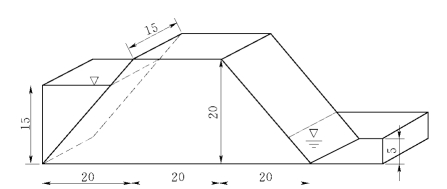
图1-7-12 土坝渗流计算示意图(单位:m)
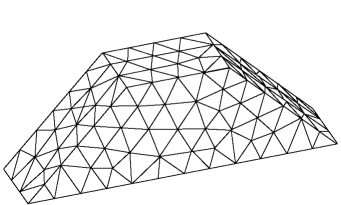
图1-7-13 初始均匀网格消隐图(559个单元,186个结点)
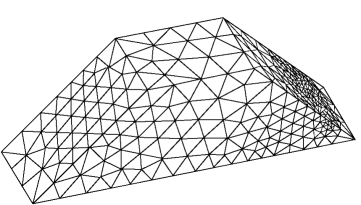
图1-7-14 最终优化网格消隐图(1606个单元,516个结点)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




