误差分析与尺度估计技巧

渗流问题的网格离散误差分析及尺度估计方法与应力应变分析的弹性问题类似（Rank，Werner，1986；Chung，Kikuchi，1987；Burkley，Bruch Jr，1991；Chen，1996）。

记水头势函数和流速的精确解为φ和{v}，有限单元法解为φh和{v h}。首先定义误差为精确解与有限单元法解的差，即

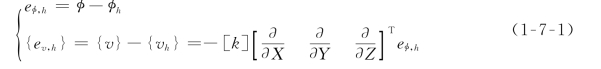
然后定义误差的能量范数对上述两种误差进行统一度量，即

式中：[k]为渗透矩阵。

由于精确解未知，只能试图用有限单元解推求一个精确解的“最佳猜测”。与弹粘塑性有限单元分析中的应力应变恢复问题类似，有一些相当精确但很复杂的方法（参见本篇第六章），下面介绍一种较简化的投影法。

有限单元法求解得到的水头函数在单元的边界连续，但是水头梯度以及流速在单元的边界处并不连续。假定存在一个精度比有限单元法解高且在单元边界连续的流速场，称为“最佳猜测”流速，记为{v*}，在误差估计中代替式（1-7-1）中的精确解。

若e等于预先设定的允许误差e t，则认为计算网格已满足精度要求，否则需进行网格优化调整。要求优化后的网格误差均匀分布于各单元内，即

(www.xing528.com)

将式（1-7-9）代入式（1-7-8），可得优化条件为

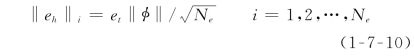
定义参数

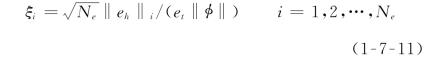
若对所有单元，有ξi=1，则网格达到最优。否则按下式求位于各单元形心点处的新的网格尺度。

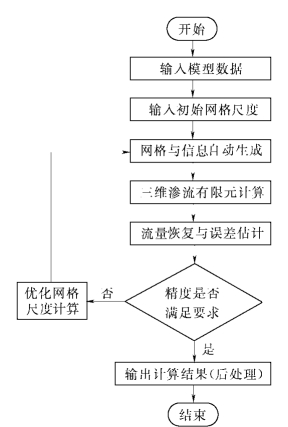
图1-7-1　三维渗流自适应有限元分析流程图

其中l=min（p，λ），p是形函数的阶数，λ是奇点的强度，且λ＜1。

根据新的网格尺度场重新调用网格生成器生成新的网格，再进行渗流有限单元计算，直至网格精度满足要求为止。

三维渗流h型自适应有限单元分析系统ASEEP包括四大模块：网格生成模块GENSEEP，渗流有限单元分析模块SEEP，网格误差及尺度场估计模块DENSEEP和后处理模块POSTSEEP。对应的流程如图1-7-1所示。