网格间数据传递技巧与优化

为方便讨论，将弹粘塑性有限单元计算中需要传递的数据记为

式中：{u h，t}为位移；{εh，t}为应变；{σh，t}为应力；{qh，t}为粘塑性内变量。下标h表示第h个网格，下标t表示处于时间的量。这些需要传递的数据通常分为两类：①位于结点的数据，如位移；②位于积分点的数据，如应力、粘塑性应变、粘塑性内变量。

一个有效的数据传递应满足下列条件：

（1）相关数据满足本构关系。

（2）相关数据满足平衡条件。

（3）新网格的位移场满足位移协调条件和位移边界条件。

在t+Δt时，得到某量Λh，t+Δt。若根据误差估计，需重新生成网格h+1，此时数据传递有两部分工作（Peric，Hochard，Dutko，Owen，1996）：

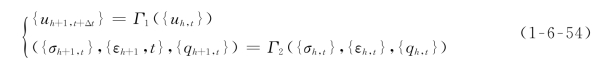
当数据传递完成后，{u h+1，t+Δt}作为第n+1步荷载的第一次迭代结果，（{σh+1，t}，{εh+1，t}，{q h+1，t}）作为弹粘塑性本构积分的初始状态，按照常规弹粘塑性有限单元计算过程进行迭代。数据传递过程Γ1只涉及新旧单元结点间数据的传递，较简单。以下对数据传递过程Γ2进行详细介绍。简记某位于高斯点的变量为Λ。

位于高斯点的数据传递方法较多，较为流行的一种方法是先将数据从高斯点转移至单元结点，然后通过新单元结点传递至新单元高斯点，具体过程如下：

第（1）步：

式（1-6-55）中，上标N、G分别表示结点和高斯点。

这一步是将数据从高斯点转移至单元结点[图1-6-5（a）]，常采用类似SPR的小片恢复法。

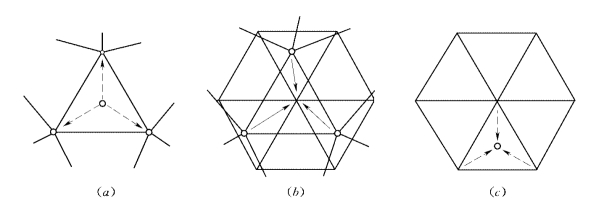
图1-6-5　数据传递过程Γ2的步骤（三角形常应变单元）

第（2）步：(www.xing528.com)

这一步是将数据从旧单元结点传递至新单元结点[图1-6-5（b）]。

对于新网格h+1中任一结点j，其整体坐标为{X h+1}j，首先需在旧网格h中找出其背景单元Ωh，e，使

然后求出结点j在Ωh，e的局部坐标{Rh}j，使

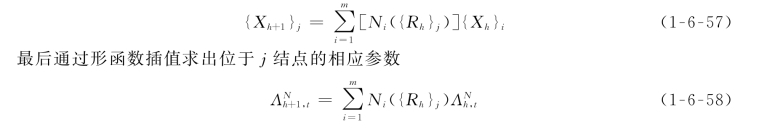
式中：m为单元结点数；N i为单元形函数。

在传递过程中，需要解决单元识别的问题，即已知一点坐标{X h+1}j，需要找到单元Ωh，e，使{X h+1}j∈Ωh，e，参见图1-6-6。该问题可通过以下方法解决。

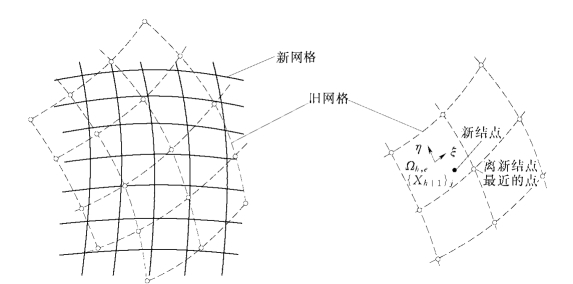
图1-6-6　单元识别

找出离点j最近的一点，并将所有与该点连接的单元作为候选单元。确定j相对每一候选单元的局部坐标{Rh}j，对于三角形（四面体），若0≤Rh，j≤1，对于四边形（六面体），若-1≤Rh，j≤1，则认为该候选单元为所寻找的单元。

局部坐标的寻找可通过一个小型的Newton-Raphson迭代实现，即

式中：m为单元结点数；{X h}i为候选单元结点坐标；N i（{Rh，j}）为形函数。

第（3）步：

新单元高斯点的参数利用形函数插值从新单元结点获得[图1-6-5（c）]，即

上述过程的第（1）步中经常用到类似SPR的小片恢复法，将高斯点的参数按最小二乘拟合传递至结点，第（2）步和第（3）步分别用有限单元形函数将参数由旧单元结点传递到新单元结点，再到新单元高斯点。最小二乘和形函数插值都不可避免地对数据产生“污染”，使变化较大的参数场被相对平均，即局部化特征被“磨平”。为了克服这个缺点，Ortiz和Quigley（1991）提出了一种将数据由旧单元高斯点直接传递至新单元高斯点的方法（Consistent Transfer Operator）。