应力恢复方法详解

有限单元后处理误差估计的方法很多，不同方法之间最主要的区别是“最佳猜测”解的获得，王建华等（王建华，杨磊，沈为平，2000）对误差估计方法有详细的评述。本节将以应力为例，重点讨论当前最为有效的两种恢复方法，并给出它们的有效性检验。

一、SPR应力恢复法

SPR法的理论基础是某些单元内存在若干应力精度较高的点（Krizek，1994）。对于一维单元和二维四边形单元，这类超收敛点的存在已有理论上的证明（见图1-6-1，小三角形表示超收敛点），故对于这些单元，SPR法通常为首选。

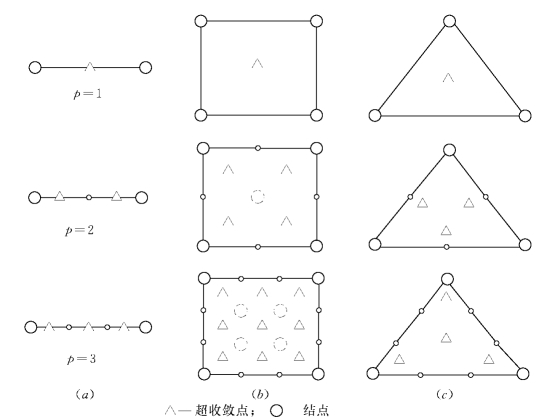
图1-6-1　一次、二次、三次单元的超收敛点

（a）杆单元；（b）四边形单元；（c）三角形单元

式中：m为小片中的单元数；k为每一单元中所有的超收敛点数。

（2）为了防止矩阵[A]产生病态，最好使用局部正则化的坐标。

设小片中任一点坐标为（X，Y，Z），满足

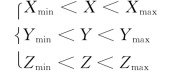
则变换后的局部坐标为

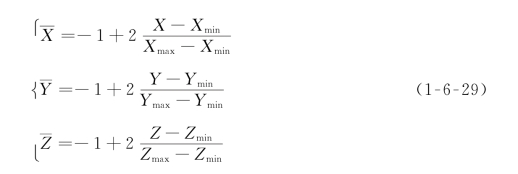
（3）对于位于网格内部的单元结点，通常会同时处于几个小片，于是利用式（1-6-28）将获得几个不同的应力值，此时可取算术平均。

SPR法提出后，又出现了多种改进方法。Wiberg和Abdulwahab于1993年提出一种基于SPR法和单元小片平衡的应力恢复法，简称W-A法，也称为SPRE法，可以认为是残值法与SPR法的结合。为解决SPR法和SPRE法在给定边界条件的边界及其临近区域误差较大的问题，Wiberg等人（Wiberg，Abdulwahab，1994；Wiberg，Li，1994）提出了SPREB法，使恢复应力满足边界条件。

二、REP应力恢复法

根据虚功原理，有限单元整体平衡方程可记为

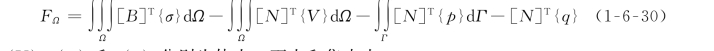
式中：{V}、{p}和{q}分别为体力、面力和集中力。

引入有限单元位移模式，平衡方程可写为

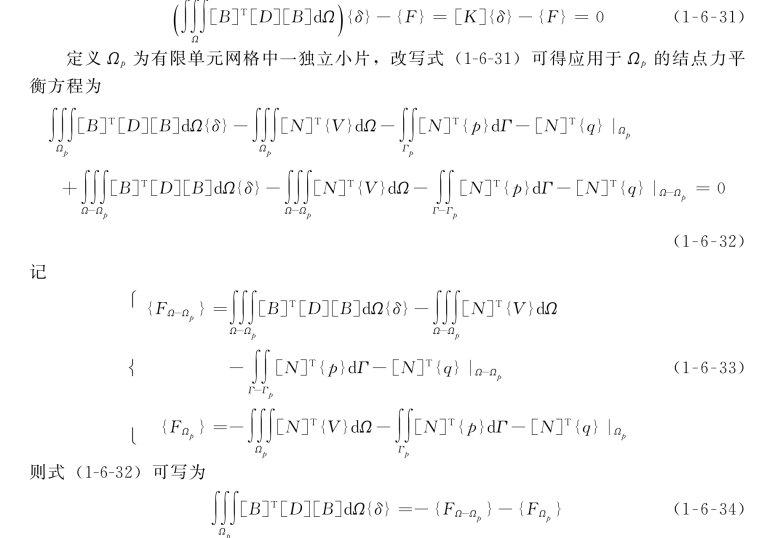
式中：{FΩ-Ωp}为网格中Ω-Ωp部分的不平衡结点力；{FΩp}为作用于Ωp上的荷载的等效结点力（图1-6-2）。

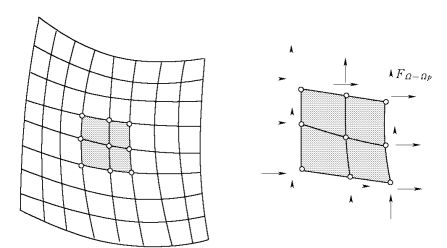
图1-6-2　REP应力恢复中的单元小片(www.xing528.com)

假设将Ωp隔离出来，施加荷载-{FΩ-Ωp}-{FΩp}，得到一个新的应力场

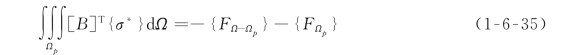
由式（1-6-34）和式（1-6-35）可得

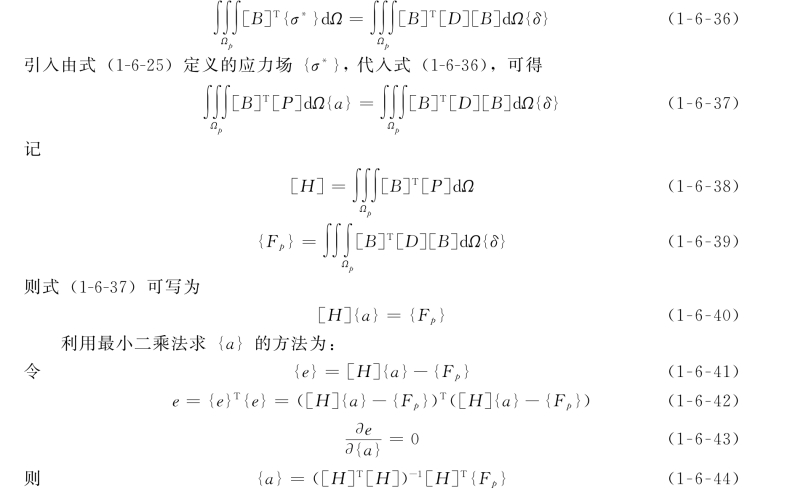
对于以上计算格式，B.Boroomand等人（1997）提出了若干修正，经过修正的计算格式，计算量显著减少，且计算稳定性有所提高。

下面简单对REP法作一些理论分析。

根据最小势能原理，对于独立小片，计算位移场应使下式取最小值

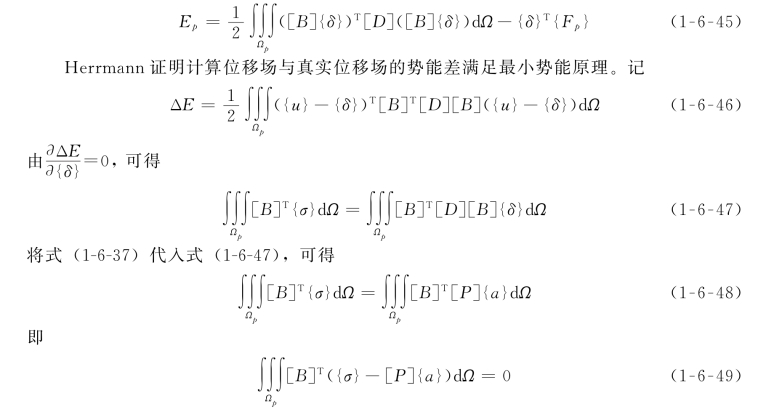
式（1-6-49）中的{σ}为真实应力场，式（1-6-24）中的{σ*}为一满足结点力平衡关系的假定应力场。式（1-6-49）表明这两者在积分形式下近似等效。同时，式（1-6-49）也表明函数[B]T对REP法的精度有很大影响。对于不同的单元类型和不同的网格，REP法得出的应力也不会完全一致。

根据计算经验，对于位于网格边界的小片，REP法得出的应力精度通常较低，这时可以添加一些边界应力平衡条件以提高应力恢复的效果，式（1-6-42）可写为

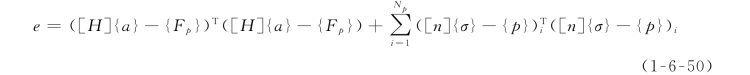
式中：{p}为边界力；[n]为应力转换矩阵；N p为边界上的积分点数。

三、误差估计有效性的检验

一般地，对有限单元网格中的单元小片Ωp进行误差估计时，Ωp及其相邻单元片的几何结构、单元片内解的光滑程度都对误差估计效果有影响，但研究发现，当Ωp和相邻单元片中单元尺寸趋于0时，误差估计的效果可以认为仅由单元片Ωp的几何结构决定。

将整个有限单元网格Ω内的全局误差估计有效性参数记为θ[式（1-6-10）]，此时存在两个常数

显然理想的误差估计有效性参数θL、θU为1，R为0。

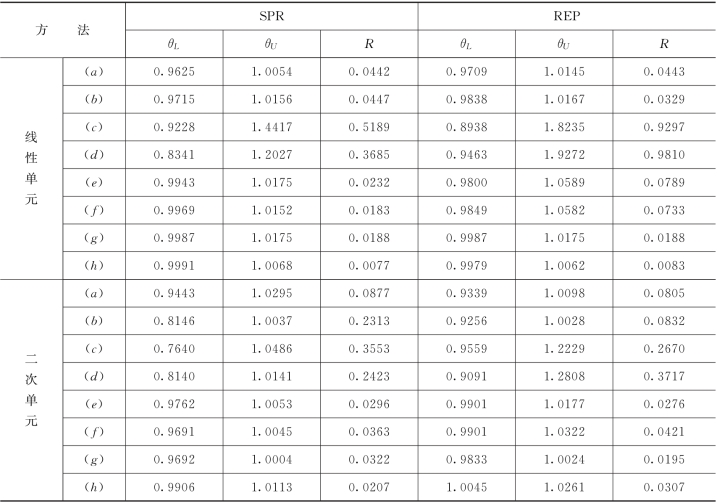
根据Babuska等人（Babuska，Strouboulis，1994）和Boroomand等人（Boroomand，Zienkiewicz，1999）的计算，有效性检验与网格的拓扑结构、有限单元解的光滑程度、单元小片的长宽比等因素有关。图1-6-3、图1-6-4为最常见的规则与不规则单元小片及其相应的周期性网格，表1-6-1给出了对于不规则单元小片的SPR、REP的有效性检验结果（Zienkiewicz，2000）。

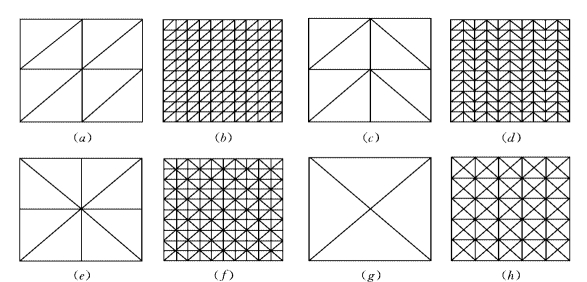
图1-6-3　规则的三角形单元小片及其周期性网格

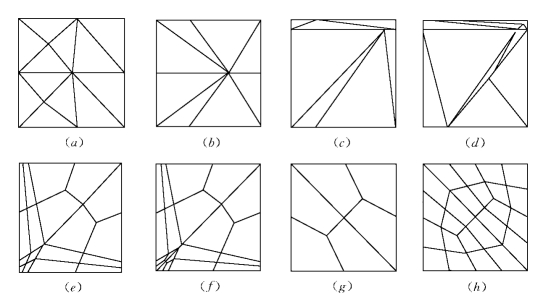
图1-6-4　不规则的三角形、四边形单元小片

表1-6-1　图1-6-4中不规则单元小片SPR、REP误差估计的有效性检验

以上内容也编入了软件模块DENCORE。