用离散型锚杆单元进行岩块拉拔数值模拟及验证

一、砂浆锚杆的拉拔试验

图1-3-13为一个5m×5m×4m（长×宽×高）的岩块，中间打入一根锚杆。用本章第二节提出的三维离散型锚杆单元，结合八结点六面体等参单元形成有限单元网格，对该岩块进行拉拔数值模拟。材料参数见表1-3-1～表1-3-3。

图1-3-13　有限元计算网格

表1-3-1　岩块的材料特性

表1-3-2　接触面的材料特性

表1-3-3　锚杆与砂浆体的材料特性

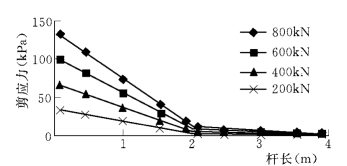
对锚杆分别施以200k N、400k N、600k N和800k N的拉拔力，弹性计算结果见图1-3-14和图1-3-15。计算结果符合以下规律：

（1）砂浆体和岩体接触面上的剪应力沿杆长递减，沿圆周方向均匀分布。

（2）锚根底部的位移和拉应力很小。

二、砂浆锚杆的直剪试验

直剪试件由混凝土制成，尺寸为220mm×200mm×150mm（Spang，Egger，1990），图1-3-16为试件的有限单元网格（在X—Z面上投影，Y方向厚度为200mm），节理水平，锚杆倾角为60°。混凝土、节理及锚杆的材料特性见表1-3-4～表1-3-6。

(www.xing528.com)

图1-3-14　砂浆体与岩体接触面的剪应力沿杆长分布

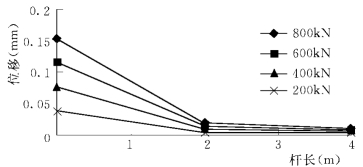
图1-3-15　锚杆与砂浆等效材料的位移沿杆长分布

图1-3-16　试件的有限单元网格

1—锚杆；2—节理

表1-3-4　混凝土的材料特性

表1-3-5　节理的材料特性

表1-3-6　锚杆的材料特性

在节理面和锚杆所在的部位采用拟等效处理，即布置一层薄层单元，其中包含节理或锚杆，根据含节理的薄层单元的厚度定义节理间距，根据含锚杆的薄层单元的体积与锚杆体积定义岩体和锚杆的体积占有率。这种方法比较简单，而且计算精度较高，在处理有较多重要结构面和锚杆的问题时优越性明显。

计算模拟的实验过程是：首先在试件顶部施加面力σ=0.2MPa，然后逐步增加剪力T，直到试件破坏。对不同的有效长度或有效高度进行试算以获得试验结果的最佳拟合，计算中有效高度的变化范围是h b=（2～4）d b，计算及试验的剪力T与水平位移u x的关系如图1-3-17所示。由图1-3-17可以看出，若有效高度能通过试验获得，则加锚节理岩体的变形和强度都可以很好地加以预测。

图1-3-17　剪切力T与水平位移u　x的关系