一、锚杆的二维离散模型
先以二维问题为例,讨论一种新的锚杆离散模型,该模型较适用于对大吨位预应力锚索内锚段及砂浆锚杆的模拟。
1989年,Aydan提出三维锚杆单元,这种单元有8个结点,其中2个位于锚杆上,6个位于岩体上,可模拟锚固件—岩体接触面的滑移特性。在二维情况下,Swoboda和Marence对Aydan模型进行了修正(Swoboda,Marence,1991;Swoboda,Marence,1992),赋予锚杆和砂浆—岩石接触面上的结点以不同的坐标,从而在锚杆与节理的交点上,锚杆与岩体有不同的位移,这样,单元弹性刚度矩阵与节理位移有关,需由子结构法迭代求解。
笔者提出一种二维六结点锚杆单元,其中锚固件与砂浆被视为一种等效连续介质,在岩体上布置4个结点以模拟接触面,在锚杆单元与节理面的交点,用简化方式模拟锚杆的力学特性(Chen,Egger,1997)。
(一)基本假定
图1-3-7是锚固件与砂浆的等效连续流变模型,包含以下基本假定:

图1-3-7 锚杆—砂浆等效流变模型
(1)荷载由锚固件和砂浆共同承担。
(2)锚固件和砂浆的变形一致。
图1-3-8是在局部坐标系中的六结点锚杆单元,各单元结点编号为:i、j位于下部岩体,k、l位于锚固件—砂浆等效材料,m、n位于上部岩体。该单元由三部分组成:锚固件—砂浆等效材料(结点k、l);锚固件—砂浆等效材料与上部岩体的接触面(结点k、l、m、n);锚固件—砂浆等效材料与下部岩体的接触面(结点i、j、k、l)。
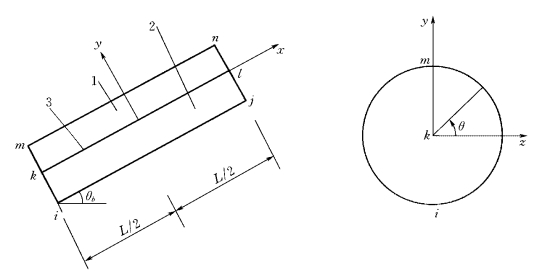
图1-3-8 六结点锚杆单元
1—上部岩体接触面;2—下部岩体接触面;3—锚固件—砂浆等效材料
(3)沿轴线方向,位移线性分布。
(4)沿半径方向,应力均匀分布。
(5)轴向力由锚固件—砂浆等效材料承担。
(6)与轴线方向垂直的剪力由锚固件—砂浆等效材料承担。
(7)沿轴线方向的剪力由锚固件—砂浆等效材料与岩体接触面承担。
(8)垂直于轴线方向,锚固件—砂浆等效材料与岩体接触面的相对位移为分段均匀分布。在锚固件—砂浆等效材料与上部岩体接触面(0°<θ<180°),该相对位移由θ=90°处的值表示;在锚固件—砂浆等效材料与下部岩体接触面(180°<θ<360°),该相对位移由θ=270°处的值表示。
(二)锚固件—砂浆等效材料的分析
1.锚固件的弹粘塑性本构关系
按基本假定(5)、(6),在锚固件—砂浆等效材料的横截面上,仅有轴力和剪力。在局部坐标系内,锚固件的隐格式弹粘塑性本构关系仍可采用式(1-1-11)~式(1-1-13)的普遍形式。
(1)粘塑性应变率。

对锚杆采用各向同性强化的Von Mises屈服准则

由于流动为关联,故锚杆的隐式弹性矩阵是对称的。
2.砂浆的弹粘塑性本构关系
同样,在局部坐标系内,砂浆的隐式弹粘塑性本构关系仍可采用式(1-1-11)~式(1-1-13)的普遍形式。
(1)粘塑性应变率。

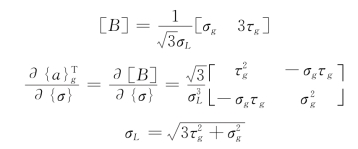
由于流动为关联,故砂浆的隐式弹性矩阵也是对称的。
3.锚固件—砂浆等效材料的弹粘塑性本构关系
按基本假定(1),可写出
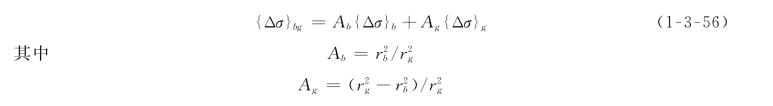
按基本假定(2),又可写出
![]()
把锚固件和砂浆的弹粘塑性本构关系代入式(1-3-56),并利用式(1-3-57),可得到锚固件—砂浆等效材料的弹粘塑性本构关系为

4.结点荷载与结点位移的关系


对式(1-3-69)积分,可得等效粘塑性荷载增量为
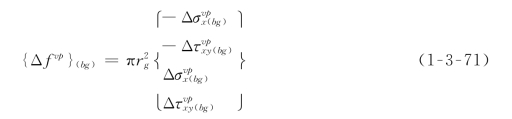
(三)锚固件—砂浆与岩体接触面的分析
1.接触面的弹粘塑性本构关系
记相对位移增量和应力增量为

则接触面的弹粘塑性本构关系为
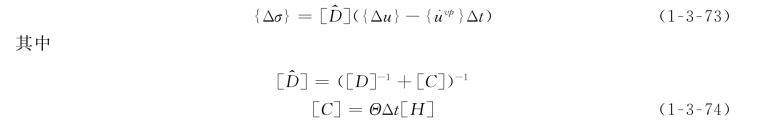
式中:[D^]为隐式弹性矩阵。
(1)粘塑性应变率。采用非关联流动法则

式中:F为屈服函数;Q为势函数;φ、φ、c和σT分别为接触面的摩擦角、剪胀角、凝聚力和抗拉强度。

由于流动是非关联的,接触面的隐式弹性矩阵不对称。可采用熊文林(1993)提出的对称化方法解决由此引起的计算不便。
2.结点荷载与结点位移的关系
(1)结触面下部。结触面下部的结点荷载与位移增量记为
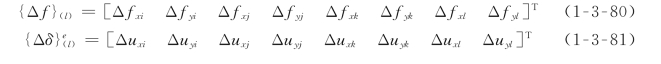

对式(1-3-85)积分后可得显格式的刚度矩阵,即
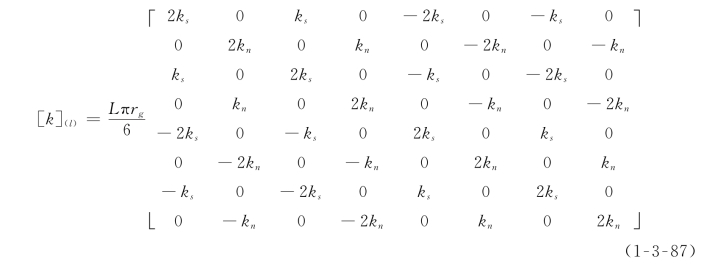
对式(1-3-86)积分,可得等效粘塑性荷载增量为
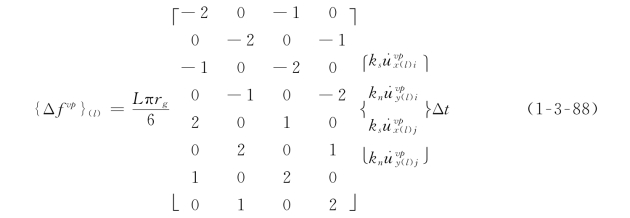
(2)结触面上部。结触面上部的结点荷载与位移增量记为

对式(1-3-93)积分,可得等效粘塑性荷载增量为
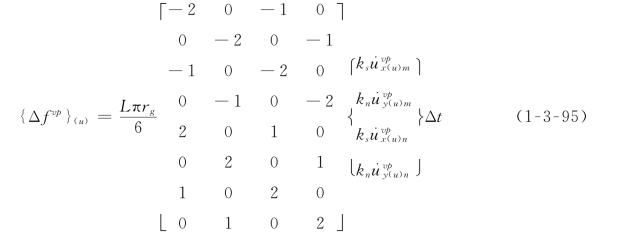
(四)锚杆单元的组合
锚杆单元的平衡方程由式(1-3-67)、式(1-3-84)及式(1-3-91)组合而成,即
![]() (https://www.xing528.com)
(https://www.xing528.com)
其中
![]()
若隐式参数Θ=0,则组合后的[k]是常刚度矩阵,即

式(1-3-96)~式(1-3-98)是在局部坐标系中给出的,若定义转换矩阵

则可得整体坐标系中的平衡方程为
![]()
其中

(五)锚杆在节理面上的行为
与式(1-3-29)~式(1-3-31)类似,假设锚杆在节理附近的变形全部集中于两铰之间的锚杆有效长度,两铰之间的相对位移等于节理面两侧岩壁的相对位移。在变形过程中,有效长度Lb和锚杆倾角θb都按下式修正
![]()
二、锚杆的三维离散模型
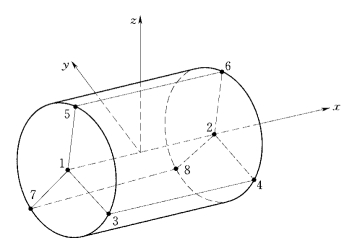
图1-3-9 三维锚杆单元示意图
在上述理论基础上,笔者提出了一种“拼装型”的三维锚杆单元模型,该单元可以模拟锚杆与岩体的接触面,且结点数可任意变化,从而克服了现有模型的局限性,比较适合加锚节理岩体的三维有限元分析(强晟,陈胜宏,2001)。为方便起见,以图1-3-9所示的八结点锚杆单元为例进行讨论。
(一)基本假定
锚固件与砂浆的等效连续流变模型仍由图1-3-7表示。基本假定为:
(1)荷载由锚固件和砂浆共同承担。
(2)锚固件和砂浆的变形相等。
(3)沿轴线方向,位移线性分布。
(4)沿半径方向,应力均匀分布。
(5)轴向力由锚固件—砂浆等效材料承担。
(6)与轴线方向垂直的剪力由锚固件—砂浆等效材料承担。
(7)沿轴线方向的剪力由锚固件—砂浆等效材料通过接触面传递到岩体。
(8)垂直于轴线方向,锚固件—砂浆等效材料与岩体接触面的相对位移为分段分布。
(二)锚固件—砂浆等效材料的分析
1.锚固件的弹粘塑性本构关系
按基本假定(5)和(6),在锚固件—砂浆等效材料的横截面上,仅有轴力和剪力。在局部坐标系内,锚固件的隐式弹粘塑性本构关系仍可采用式(1-1-11)~式(1-1-13)的普遍形式。
(1)粘塑性应变率。

由于流动为关联,故锚杆的隐式弹性矩阵是对称的。
2.砂浆的弹粘塑性本构关系
(1)粘塑性应变率。
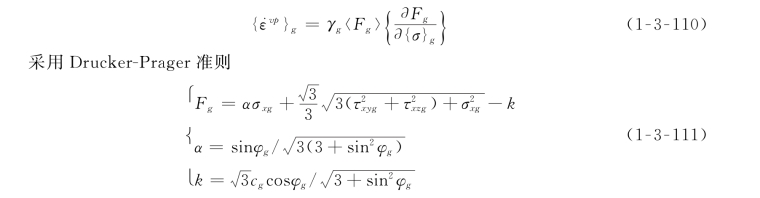
式中:c g、φg分别为砂浆的凝聚力和内摩擦角。


(三)锚固件-砂浆与岩体接触面的分析
1.接触面的弹粘塑性本构关系
记相对位移增量和应力增量为(图1-3-10)
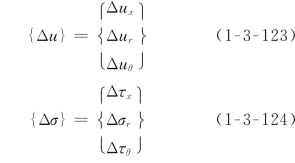
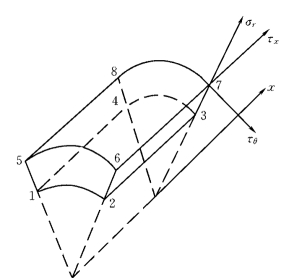
图1-3-10 接触面节理单元示意图
则接触面的弹粘塑性本构关系为
![]()
其中

![]()

由于流动是非关联的,接触面的隐式弹性矩阵不对称,此时可采用熊文林(1993)提出的对称化方法解决由此引起的计算不便。
2.结点荷载与结点位移的关系
结点荷载与位移增量记为

(四)锚杆单元的组合
一般情况下,锚杆单元由一个代表锚固件—砂浆的杆单元和代表分片接触面的nj个节理单元拼装而成,n j视该锚杆单元与周边岩体单元的接触情况而定。杆单元与节理单元的组合规则为(图1-3-11):假定杆单元的结点号为I、J,则每个节理单元的内壁结点(图1-3-10中结点1、2、3、4)分别凝聚到结点I、J上;相邻两个节理单元的相邻外壁结点凝聚为一点。

图1-3-11 锚杆单元组合示意图
三、预应力锚索的三维离散力学模型
锚索本身是一种柔性构件,在受拉时才产生作用。预应力锚索加固岩体的优点在于能为岩体边坡提供一种强有力的主动支护手段(黄福德,赵彦辉,1996;宋安成,2002)。尽管预应力锚固的工程经验日益成熟,但在预应力锚索的作用模拟研究方面仍处于不很成熟的阶段。
预应力锚索可分为三部分:外锚头、内锚段和自由段。自由段也有采取二次灌浆进行防锈保护的。大规模预应力锚索的模拟有两个基本问题:预应力的施加和锚固件的单元模型。
预应力施加的常规方法是:在外锚头部位,施加集中力或某种假定图形的分布力;在内锚段部位,施加集中力。在内锚段由于集中力施加的部位很难确定,通常假定作用于内锚段与自由段的交界部位。这种处理低估了锚固效果,但偏于安全。
外锚头在结构中的效应通常不予考虑。内锚段则因有拔出破坏等问题,应该在结构分析中进行模拟,可采用本章第一节介绍的锚杆等效方法模拟,也可采用本章第二节介绍的锚杆离散方法模拟。
当自由段没有二次灌浆时,可以按锚索单元模拟其对结构刚度的贡献。图1-3-12表示的是联系单元ei和e j的锚索单元c。
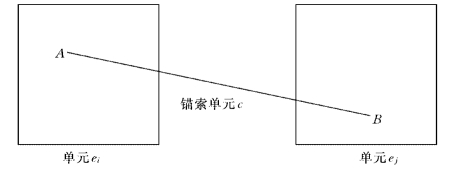
图1-3-12 锚索单元AB
(1)几何参数。走向φc、倾角θc;外锚端点A位于单元e i内,整体坐标为(X ci,Y ci,Zci),局部坐标为(ξci,ηci,ζci);内锚端点B位于单元e j内,整体坐标为(X cj,Y cj,Zcj),局部坐标为(ξcj,ηcj,ζcj);截面积A c、长度l c。
(2)力学参数和变量。弹性模量E c、内力增量ΔRc、变形增量Δδc。
点A和点B的位移增量可以表示为


本节介绍的本构关系由有限单元法程序CORE实现。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




