如何进行岩体等效模拟之加锚节点优化

一、流变模型的考虑

1.基本原则

图1-3-1　通常的流变模型

锚固件与节理岩体的相互作用机理和力学模型是加锚节理岩体研究的基础之一。在系统锚杆方案中，锚杆对已有或新产生的节理裂隙的限剪和限裂是其加固作用的主要机理，力学模型应能加以反映。对预应力长锚索，在张拉阶段内锚段与围岩的相互作用、传力方式、破坏机理以及二次灌浆后全锚索在围岩中的作用等问题，也有赖于正确的力学模型。

国内外很多学者对加锚节理岩体的模拟计算方法进行了研究，其中Pande等人（Sharma，Pande，1988）的成果较系统，也较实用，其流变模型如图1-3-1所示，优点是简单易行，缺点是与真实加固机理差距较大。

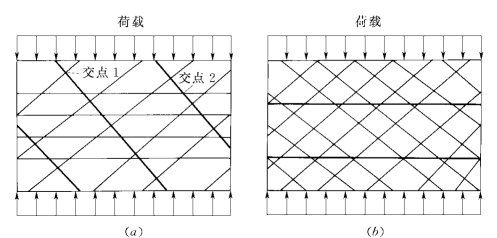
图1-3-2　含两组节理一组锚杆的代表单元

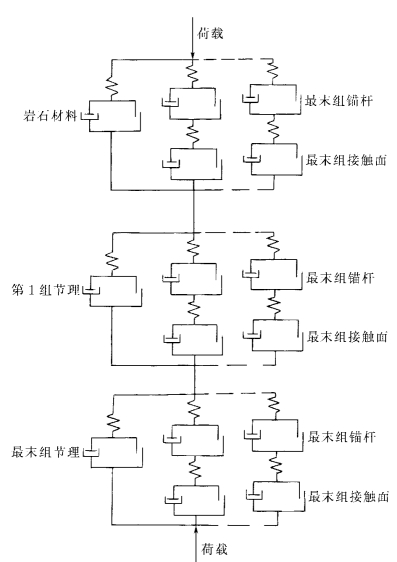
图1-3-3　新的流变模型

考虑图1-3-2（a）所示的代表单元，内含两组节理和一组锚杆，受均匀铅直荷载作用。在锚杆与第1组和第2组节理的交点1和交点2上，由于变形条件不同，锚杆的应力也不同，而按图1-3-1所示的模型，锚杆应力在代表单元内被均化，不能反映这种差别。再考察图1-3-2（b）所示的代表单元，两组节理倾角都是45°，物理力学参数也相同，锚杆水平布置，则在均匀铅直荷载作用下，没有宏观剪应力产生，从而按图1-3-1的流变模型，锚杆仅受拉应力，不存在剪应力。实际上，由于局部剪切变形的存在，在锚杆与节理面的交点，锚杆除受拉外，还受剪切作用。忽视这种局部化应力将会过低估计锚杆的应力，从而低估锚杆的作用。

为了更好地反映加锚节理岩体的变形和破坏机理，笔者提出了图1-3-3所示的流变模型（Chen，Pande，1994；Chen，Egger，1999）。

该模型隐含以下4条基本原则：

（1）应变叠加原则。加锚节理岩体的应变增量等于加锚岩块与各组加锚节理的应变增量之和。

（2）应力分担原则。加锚岩块中，应力增量由岩块和锚杆共同承担；加锚节理中，应力增量由节理和锚杆共同承担。

（3）应力一致原则。加锚节理岩体与加锚岩块及各组加锚节理的应力增量一致。

（4）应变一致原则。加锚岩块中，锚杆的应变与岩块的应变一致；加锚节理中，锚杆的应变与节理的应变一致。

推导本构关系时，可根据不同的岩石类型，在以上流变模型中引入不同的节理裂隙变形和破坏机制。例如，若考虑岩体中小尺度非贯通节理裂隙，则可用损伤力学模型；若主要关注大尺度节理面或大坝结构的结触面，则可用一般Goodman模型（Goodman，Taylor，Brekke，1968）描述其拉剪和压剪变形破坏。以下主要讨论后一种情况。

2.坐标与转换

定义整体坐标系的X轴朝北，Y轴朝西，Z轴朝上。加锚节理岩体的本构方程将在整体坐标系中建立。

为方便公式的推导，对每组节理和锚杆都建立其各自的局部坐标系。对节理面j，z j轴垂直于节理面，y j轴指向节理面倾向，x j轴与z j轴、y j轴成右手螺旋系；对锚杆b，zb轴与锚杆轴向一致，y b轴指向锚杆倾向，x b轴与z b轴、y b轴成右手螺旋系。在将要涉及到的公式中，没有下标的量表示等效后的加锚节理岩体；下标r、j和b分别表示岩块、第j组节理和第b组锚杆；下标（br）、（bj）分别表示岩块中的锚杆和第j组节理中的锚杆；下标r（b）、j（b）分别表示加锚岩块和第j组加锚节理。所有下标中，小写字母表示在局部坐标系下的量，大写字母表示在整体坐标系下的量。

定义整体坐标系和局部坐标系下应力和应变的相互转换关系为

式中：l ij为转换矩阵[L]的分量。

对第j组节理，有

式中：φj、θj分别为节理的倾向和倾角；φb、θb分别为锚杆的倾向和倾角。

在节理和锚杆局部坐标系之间，应力和应变的转换定义为

3.流变模型基本原则的公式化

在弹粘塑性有限单元计算中，在任一时间t，新流变模型的4条基本原则可分别用公式表示。

二、加锚节理岩体各组分的隐式弹粘塑性本构关系

为建立加锚节理岩体的隐式弹粘塑性本构关系，首先需建立各组分的隐式弹粘塑性本构关系，然后按流变模型的4条基本原则进行组合。

各组分的隐式弹粘塑性本构关系均可写为式（1-1-11）～式（1-1-13）的普遍形式。对岩石、节理和锚杆，可分别进行以下的本构关系具体化工作。

（一）岩块的隐式弹粘塑性本构关系

1.粘塑性应变率

对岩块采用Drucker-Prager屈服准则

式中：φR、c R分别为内摩擦角和凝聚力。

假定关联流动法则成立，即(www.xing528.com)

其中

由于流动为关联，故隐式弹性矩阵是对称的。

（二）节理的隐式弹粘塑性本构关系

1.粘塑性应变率

由于流动为非关联，故节理的隐式弹性矩阵是非对称的，从而导致刚度矩阵的非对称性，这时可采用熊文林（1993）提出的方法进行对称化处理。

（三）锚杆的隐式弹粘塑性本构关系

1.节理上的锚杆

锚杆在节理面附近的行为非常复杂。Egger等人对加锚节理岩体作了大量的实验室和现场试验（Egger，Fernandes，1983；Spang，Egger，1990；Egger，Zabuski，1991；Egger，Pellet，1991）。其中，实验室直剪试验的试件尺寸分别为220mm×200mm×150mm和150mm×150mm×130mm，图1-3-4是试验装置。

通过试验得出以下主要结论：

（1）当锚杆与节理法线的交角较小时，锚杆弯曲非常强烈，从而在节理面两侧形成铰。由于两铰之间的锚杆应力几乎是均匀的，故锚杆的破坏位置不能确定。破坏可能发生于其中的一个塑性铰，也可能发生于节理面附近的拉剪。在相同的试验条件下，两种破坏都可能发生，但加锚节理的极限强度和对应的位移却几乎一致。

（2）当锚杆与节理法线的交角较大时，锚杆弯曲也会在节理面两侧形成铰，但并不强烈，大部分试件的破坏发生于节理面附近的拉剪。

（3）弯曲锚杆的高度h b约等于锚杆直径d b的2～4倍，即h b≈（2～4）d b，该高度称为有效高度，对应的有效长度为L b=hb/cosαb（图1-3-5），有效高度与岩石（或砂浆）的材料特性、锚杆的材料特性、锚杆的直径、锚杆的倾角等因素有关。

假定沿着有效长度，轴向力σb为均匀分布，剪切力τb为均匀分布或三角形分布，如图1-3-6所示。

在该有效长度内，锚杆用“真实”应力和应变表达的本构方程为

图1-3-4　直剪试验装置

1—块体；2—刚性盒；3—锚杆；4—砂浆；5—剪切面；6—铅直千斤顶；7—无摩擦上支承；8—导向环；9—块体千斤顶；10—剪力传感器；11—剪切位移传感器；12—法向力传感器；13—铅直位移传感器

图1-3-5　锚杆在节理面的变形

图1-3-6　锚杆有效长度内的应力分布

（1）粘塑性应变率。锚杆采用各向同性强化的Von Mises屈服准则

2.岩石中的锚杆

（1）粘塑性应变率。

三、加锚节理岩体的等效隐式弹粘塑性本构关系

把每个构件的本构方程代入式（1-3-8），并实施由式（1-3-1）～式（1-3-6）定义的变换，可得加锚岩块和加锚节理的本构方程为

其中

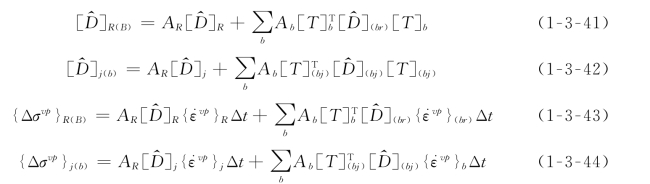
把式（1-3-39）和式（1-3-40）获得的加锚节理的本构方程用式（1-3-1）定义的矩阵[T]j加以变换，然后与加锚岩块的本构方程一起代入方程（1-3-7），即得到加锚节理岩体的弹粘塑性本构方程为

本节介绍的本构关系由有限单元法程序CORE实现。